内接円の中心が描く軌跡／媒介変数と回転体の体積(神戸大2020理系第2問)

内接円の中心の座標

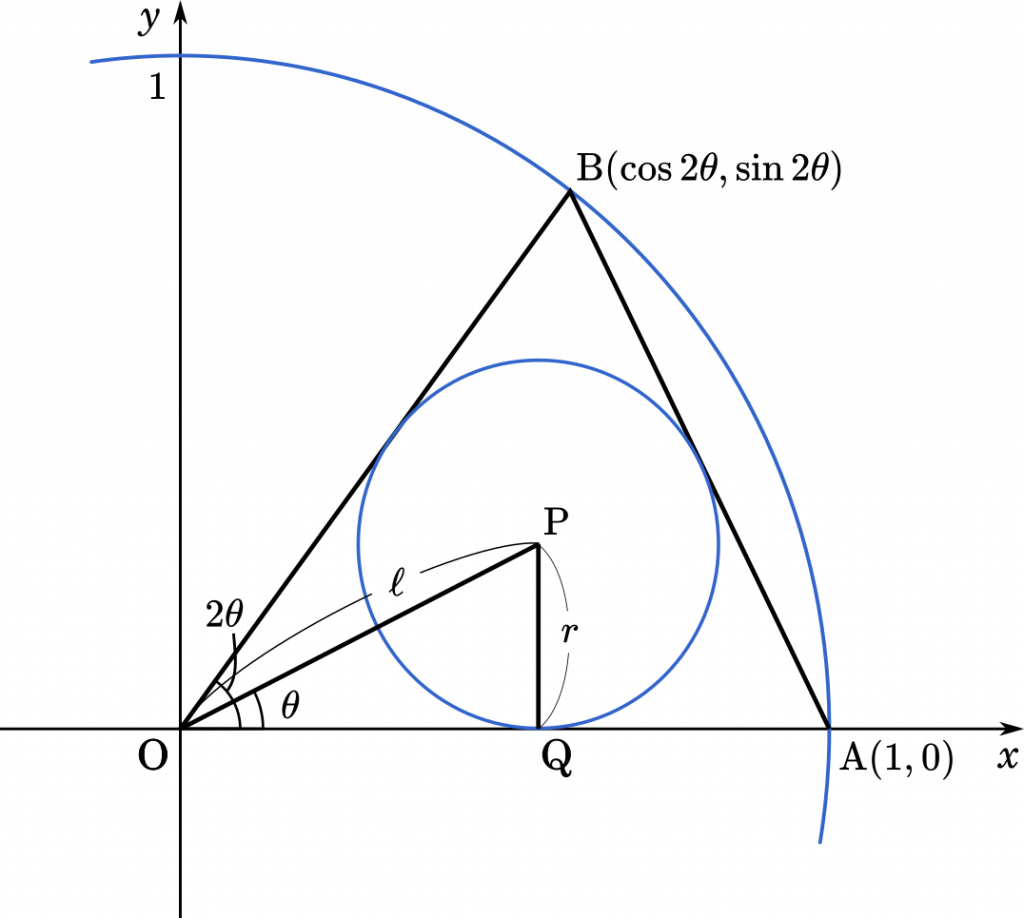
このように図を描いてみると，△OPQ のそれぞれの辺の長さがわかれば，点 P の座標が求められそうです。

これを使って $r$ を求めたいのですが，そのためには $r$ 以外の値がわかっていなければなりません。

まず △OAB は底辺が 1，高さが $\sin2\theta$ なので，面積は

$S=\cfrac{1}{2}\cdot1\cdot\sin2\theta$
$=\cfrac{1}{2}\sin2\theta$

となります。

また，△OAB は OA ＝ OB の二等辺三角形で辺の長さは 1 です。あとは AB の長さが必要なので，余弦定理で求めましょう。

$\text{AB}^2=1^2+1^2-2\cdot1\cdot1\cdot\cos2\theta$
$=2-2\cos2\theta$
$=2(1-\cos2\theta)$

$=4\cdot\cfrac{1-\cos2\theta}{2}$
$=4\sin^2\theta$
$\text{AB}=2\sin\theta$

最初の公式にもどりましょう。

$S=\cfrac{1}{2}r(a+b+c)$ より

$\cfrac{1}{2}\sin2\theta=\cfrac{1}{2}r(1+1+2\sin\theta)$
$r=\cfrac{\sin2\theta}{2+2\sin\theta}$

$=\cfrac{2\sin\theta\cos\theta}{2+2\sin\theta}$
$=\cfrac{\sin\theta\cos\theta}{1+\sin\theta}$

このとき $r$ が点 P の $y$ 座標ということになります。

あとは三角比を使って OQ の長さを求めます。

$\cfrac{r}{\text{OQ}}=\tan\theta$ より

$\cfrac{r}{\text{OQ}}=\cfrac{\sin\theta}{\cos\theta}$
$\text{OQ}=\cfrac{\cos\theta}{\sin\theta}\cdot r$
$=\cfrac{\cos\theta}{\sin\theta}\cdot\cfrac{\sin\theta\cos\theta}{1+\sin\theta}$
$=\cfrac{\cos^2\theta}{1+\sin\theta}$
$=\cfrac{1-\sin^2\theta}{1+\sin\theta}$
$=\cfrac{(1+\sin\theta)(1-\sin\theta)}{1+\sin\theta}$
$=1-\sin\theta$

したがって

点 P の座標は $\Big(1-\sin\theta,\cfrac{\sin\theta\cos\theta}{1+\sin\theta}\Big)$

（答え）

回転体の体積

点 P の座標は(1)で $\Big(1-\sin\theta,\cfrac{\sin\theta\cos\theta}{1+\sin\theta}\Big)$ となっていますが，このままでは $\theta$ の値が変化するときに，点 P がどのような曲線をつくるのかがイマイチわかりません。

そこで，いったん増減表をつくって点 P が描く曲線の概形を考えてみましょう。

$x=1-\sin\theta$
$y=\cfrac{\sin\theta\cos\theta}{1+\sin\theta}$

として

$\cfrac{dx}{d\theta}=-\cos\theta$

$\cfrac{dy}{d\theta}=\cfrac{(\sin\theta\cos\theta)'(1+\cos\theta)-\sin\theta\cos\theta(1+\sin\theta)’}{(1+\sin\theta)^2}$

$(\sin\theta\cos\theta)’$ の部分は積の微分を使います。

$=\cfrac{(\cos^2\theta-\sin^2\theta)(1+\sin\theta)-\sin\theta\cos^2\theta}{(1+\sin\theta)^2}$

式を $\sin$ に合わせていきます。

$=\cfrac{(1-\sin^2\theta-\sin^2\theta)(1+\sin\theta)-\sin\theta(1-\sin^2\theta)}{(1+\sin\theta)^2}$
$=\cfrac{(1-2\sin^2\theta)(1+\sin\theta)-\sin\theta+\sin^3\theta}{(1+\sin\theta)^2}$
$=\cfrac{1+\sin\theta-2\sin^2\theta-2\sin^3\theta-\sin\theta+\sin^3\theta}{(1+\sin\theta)^2}$
$=\cfrac{-\sin^3\theta-2\sin^2\theta+1}{(1+\sin\theta)^2}$

ここで，いったん $\sin\theta=k$ とすると

$=-\cfrac{k^3+2k^2-1}{(1+k)^2}$

因数分解します。

$k=-1$ のとき，$k^3+2k^2-1=0$ となるので，$k^3+2k^2-1$ は $k+1$ で因数分解できます。

組立除法を用いて

$\begin{matrix}1&2&0&-1&|\underline{-1}\\&-1&-1&1\\\hline 1&1&-1&0\end{matrix}$

$=-\cfrac{(k+1)(k^2+k-1)}{(1+k)^2}$
$=-\cfrac{k^2+k-1}{1+k}$
$=-\cfrac{\sin^2\theta+\sin\theta-1}{1+\sin\theta}$

極値を求めます。

$\cfrac{dx}{d\theta}$ について

$-\cos\theta=0$ とすると

$\theta=\cfrac{\pi}{2}$

$\cfrac{dy}{d\theta}$ について

$-\cfrac{\sin^2\theta+\sin\theta-1}{1+\sin\theta}=0$ とすると

$\sin^2\theta+\sin\theta-1=0$

$0<\theta<\cfrac{\pi}{2}$ より

$\sin\theta=\cfrac{-1+\sqrt{5}}{2}$

増減表は

$\def\arraystretch{1.5}\begin{array}{|c||c|c|c|c|c|}\hline\theta&(0)&\cdots&\alpha&\cdots&(\frac{\pi}{2})\\\hline\frac{dx}{d\theta}&(-1)&-&&-&(0)\\\hline x&(1)&\searrow&&\searrow&(0)\\\hline \frac{dy}{d\theta}&(1)&+&0&-&(-\frac{1}{2})\\\hline y&(0)&\nearrow&\frac{-1+\sqrt{5}}{2}&\searrow&(0)\\\hline\end{array}$

点 P の描く曲線はオレンジの部分になります。

回転体の体積を求めましょう。

$\displaystyle S=\int_0^1\pi y^2dx$

ただし，$y=\cfrac{\sin\theta\cos\theta}{1+\sin\theta}$ なので，$\theta$ の式を $x$ で積分することはできません。そこで $dx$ を $d\theta$ に置換しましょう。

$x=1-\sin\theta$ より

$dx=-\cos\theta\space d\theta$

$\def\arraystretch{1.5}\begin{array}{c|c}x&0\rightarrow1\\\hline\theta&\frac{\pi}{2}\rightarrow0\end{array}$

$\displaystyle=\pi\int_{\small{\frac{\pi}{2}}}^0\cfrac{\sin^2\theta\cos^2\theta}{(1+\sin\theta)^2}\cdot(-\cos\theta)d\theta$
$\displaystyle=-\pi\int_{\small{\frac{\pi}{2}}}^0\cfrac{\sin^2\theta\cos^3\theta}{(1+\sin\theta)^2}\space d\theta$

積分区間をひっくり返しておきましょう。

$\displaystyle=\pi\int_0^{\small{\frac{\pi}{2}}}\cfrac{\sin^2\theta\cos^3\theta}{(1+\sin\theta)^2}\space d\theta$

このまま積分していっても良いのですが，おそらく計算式が複雑なことになります。そこでもう一度置換して計算しやすくしておきましょう。

$\sin\theta=t$ とすると

$\cos\theta\space d\theta=dt$

$\def\arraystretch{1.5}\begin{array}{c|c}\theta&0\rightarrow\frac{\pi}{2}\\\hline t&0\rightarrow1\end{array}$

$\cos^3\theta$ の部分は

$\cos^3\theta=\cos^2\theta\cdot\cos\theta$
$=(1-\sin^2\theta)\cos\theta$

と変形できるので

$=\displaystyle\pi\int_0^1\cfrac{t^2(1-t^2)}{(1+t)^2}\space dt$
$=\displaystyle\pi\int_0^1\cfrac{t^2(1+t)(1-t)}{(1+t)^2}\space dt$
$=\displaystyle\pi\int_0^1\cfrac{t^2(1-t)}{1+t}\space dt$
$=\displaystyle\pi\int_0^1\cfrac{t^2-t^3}{1+t}\space dt$

ここで

$\cfrac{t^2-t^3}{1+t}$
$=\cfrac{t^2}{1+t}-\cfrac{t^3}{1+t}$
$=\cfrac{t^2-1+1}{1+t}-\cfrac{t^3+1-1}{1+t}$
$=\cfrac{(t+1)(t-1)+1}{1+t}-\cfrac{(t+1)(t^2-t+1)-1}{1+t}$
$=t-1+\cfrac{1}{1+t}-t^2+t-1+\cfrac{1}{1+t}$
$=-t^2+2t-2+\cfrac{2}{1+t}$

となるので

$\displaystyle S=\pi\int_0^1-t^2+2t-2+\cfrac{2}{1+t}\space dt$
$=\pi\Big[-\cfrac{t^3}{3}+t^2-2t+2\log(1+t)\Big]_0^1$
$=\pi\Big(-\cfrac{1}{3}+1-2+2\log 2\Big)$
$=\pi\Big(2\log2-\cfrac{4}{3}\Big)$　（答え）