x と y を t の式で表すとき(媒介変数表示)の微分・グラフ・面積の求め方が基本からわかる！練習問題(神戸大2019理系第5問)

媒介変数表示

$$x=\sin t,y=(1+\cos t)\sin t\space\space\space\space(0\leqq t\leqq\pi)$$

で表される曲線を $C$ とする。以下の問に答えよ。

(1) $\cfrac{dy}{dx}$ および $\cfrac{d^2y}{dx^2}$ を $t$ の関数として表わせ。

(2) $C$ の凹凸を調べ，$C$ の概形を描け。

(3) $C$ で囲まれる領域の面積 $S$ を求めよ。

媒介変数表示の微分

(1)から始めます。

$\cfrac{dy}{dx}$ は式を $x$ で微分するということです。しかし，$x=\sin t$ は右辺が $t$ の式です。

右辺が $t$ の式であるなら，$t$ で微分するしかありません。

$x=\sin t$ を $t$ で微分すると

$\cfrac{dx}{dt}=\cos t$

また

$\cfrac{dy}{dt}=-\sin^2 t+(1+\cos t)\cos t$

公式 $\sin^2x+\cos^2x=1$ を用いて，式を $\cos$ に合わせておきましょう。

$=-(1-\cos^2t)+\cos t+\cos^2t$
$=2\cos^2t+\cos t-1$

ここからは教科書に書いてあったことを思い出しましょう。

$\cfrac{dy}{dx}=\cfrac{\cfrac{dy}{dt}}{\cfrac{dx}{dt}}=\cfrac{2\cos^2t+\cos t-1}{\cos t}$
$=2\cos t+1-\cfrac{1}{\cos t}$　（答え）

次に進みます。

$\cfrac{d^2y}{dx^2}$ は第二次導関数と言って，$\cfrac{dy}{dx}$ をさらに $x$ で微分したものです。

ここは合成関数の微分の考え方を用います。

$\cfrac{dy}{dx}$ を $x$ で微分すると

$\cfrac{dt}{dx}\cdot\cfrac{d}{dt}\cdot\cfrac{dy}{dx}$

どういうことか説明します。まず，$\cfrac{dy}{dx}$ は $t$ で微分するしかないので $\cfrac{d}{dt}$ を付けて $t$ で微分します。そして，$\cfrac{dt}{dx}$ をつけると $dt$ どうしが約分されて $dx$ が残るということです。

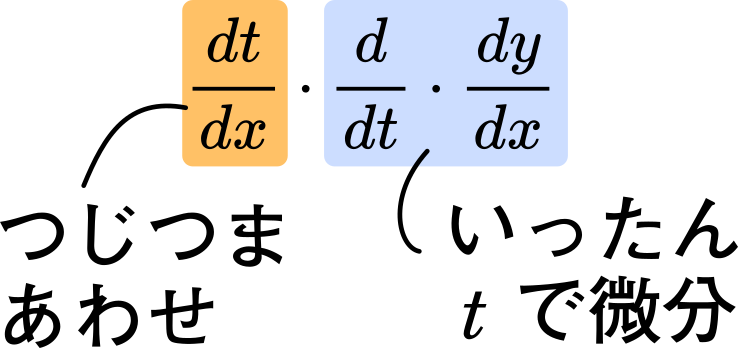
$\cfrac{\cancel{dt}}{dx}\cdot\cfrac{d}{\cancel{dt}}\cdot\cfrac{dy}{dx}=\cfrac{d^2y}{dx^2}$

ちょっとした細工が必要ですが，こうすれば $x$ で微分したということになります。

$\cfrac{dt}{dx}$ は先ほど求めた $\cfrac{dx}{dt}$ の逆数です。

$\cfrac{dt}{dx}=\cfrac{1}{\cos t}$　・・・①

また

$\cfrac{d}{dt}\cdot\cfrac{dy}{dx}=-2\sin t-\cfrac{\sin t}{\cos^2t}$　・・・②

①，②より

$\cfrac{dt}{dx}\cdot\dfrac{d}{dt}\cdot\cfrac{dy}{dx}=\cfrac{1}{\cos t}\Big(-2\sin t-\cfrac{\sin t}{\cos^2t}\Big)$

$\cfrac{d^2y}{dx^2}=-\cfrac{2\sin t}{\cos t}-\cfrac{\sin t}{\cos^3t}$
$=-\cfrac{\sin t(2\cos^2 t+1) }{\cos^3 t}$

（答え）

増減表とグラフを描く

(2)に進みます。それぞれの関数を調べて増減表をつくりましょう。問題文より範囲は $0\leqq t\leqq\pi$ です。

まず，$\cfrac{dx}{dt}$ から

$\cos t=0$ とすると

$t=\cfrac{\pi}{2}$

$\cfrac{dy}{dt}$ について

$2\cos^2t+\cos t-1=0$ とすると

$(2\cos t-1)(\cos t+1)=0$
$\cos t=\cfrac{1}{2},-1$
$t=\cfrac{\pi}{3},\pi$

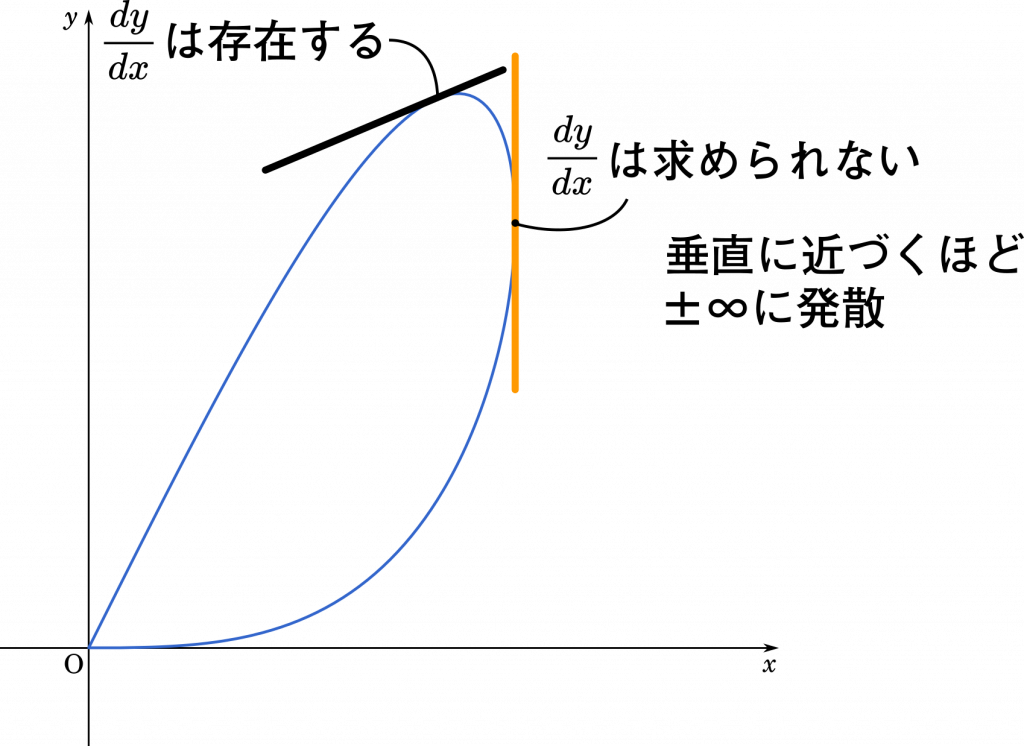
$\cfrac{dy}{dx}$ について

$2\cos t+1-\cfrac{1}{\cos t}=0$ とすると

式から $\cos t\not=0$，つまり $t\not=\cfrac{\pi}{2}$ という条件が出てきます。

$\cos t\not=0$ として，両辺に $\cos t$ をかけると

$2\cos^2 t+\cos t-1=0$
$t=\cfrac{\pi}{3},\pi$

$\cfrac{d^2}{dx^2}$ について

$-\cfrac{\sin t(2\cos^2 t+1) }{\cos^3 t}=0$ とすると

これも $\cos t\not=0$ から $t\not=\cfrac{\pi}{2}$ となります。

$\sin t=0$ とすると

$t=0,\pi$

$2\cos^2t+1=0$ とすると
$\cos^2t=-\cfrac{1}{2}$

左辺は 2 乗しているのでつねに正の数です。よって，$-\cfrac{1}{2}$ になることはないので解なしです。

増減表は

$\def\arraystretch{1.5}\begin{array}{|c||c|c|c|c|c|c|c|}\hline t&0&\cdots&\frac{\pi}{3}&\cdots&\frac{\pi}{2}&\cdots&\pi\\\hline \frac{dx}{dt}&1&+&&+&0&-&-1\\\hline x&0&\nearrow&\frac{\sqrt{3}}{2}&\nearrow&1&\searrow&0\\\hline\frac{dy}{dt}&2&+&0&-&-1&-&0\\\hline y&0&\nearrow&\frac{3\sqrt{3}}{4}&\searrow&1&\searrow&0\\\hline\frac{dy}{dx}&2&+&0&-&/&+&0\\\hline\frac{d^2y}{dx^2}&0&-&-&-&/&+&0\\\hline\end{array}$

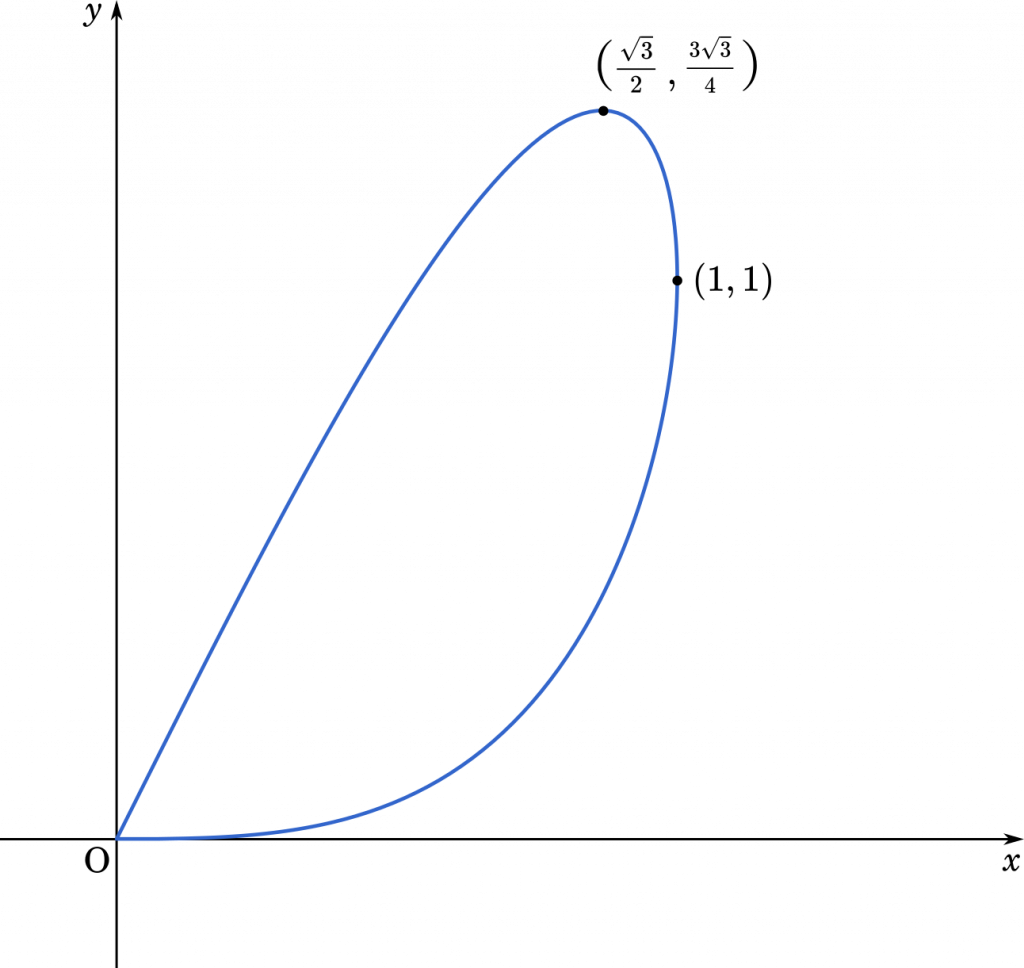
（答え）

グラフは原点からスタートし，$\Big(\cfrac{\sqrt{3}}{2},\cfrac{3\sqrt{3}}{4}\Big)$ を通ったあと，$t=\cfrac{\pi}{2}$ で $(1,1)$ を通ります。そして，$t=\pi$ で再び原点に戻ります。

面積を求める

(3)に進みます。

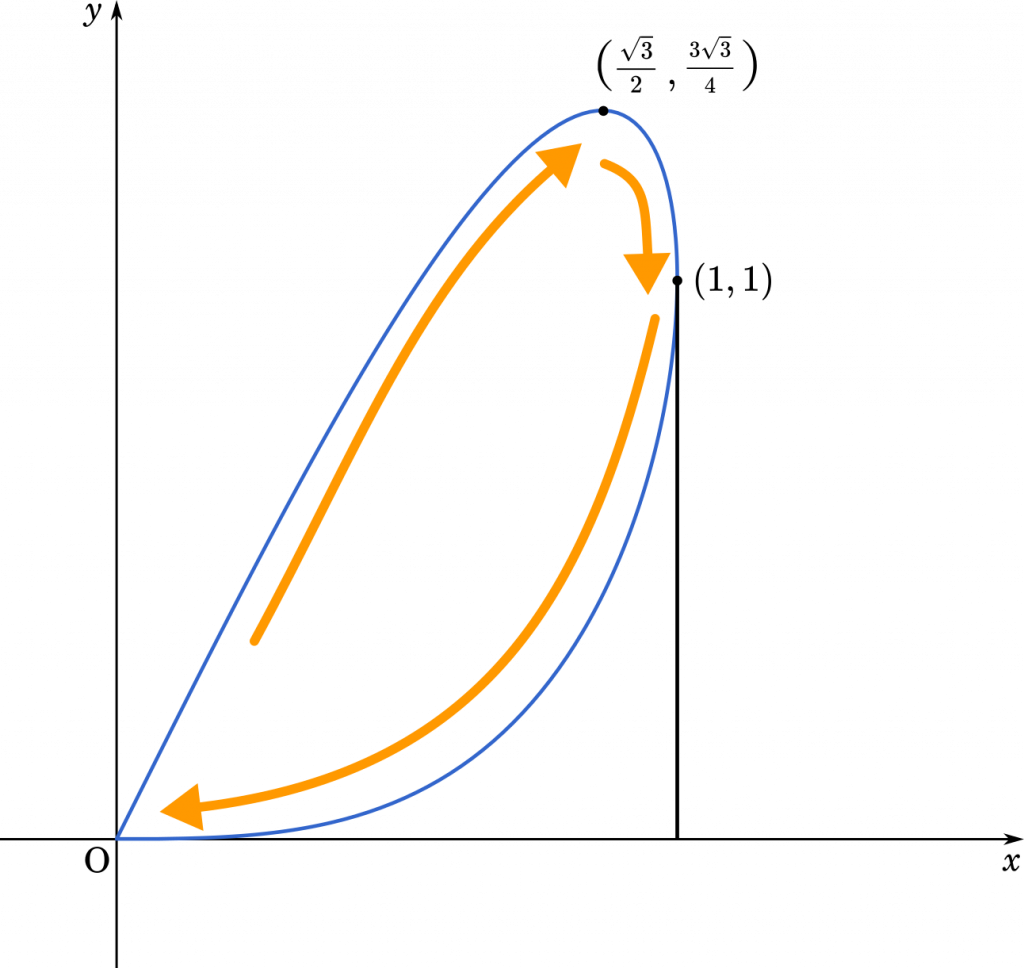
面積は上のように引き算で求めます。

まず青色の部分の面積は

$\displaystyle S_1=\int_0^\frac{\pi}{2} (1+\cos t)\sin t\space dx$

となります。次にオレンジの部分の面積は

$\displaystyle S_2=\int_\frac{\pi}{2}^\pi (1+\cos t)\sin t\space dx$

となります。

式の文字と積分する文字が異なるときは置換積分で対処します。

$x=\sin t$ より

$dx=\cos t\space dt$

$S_1$ の区間は

$\def\arraystretch{1.5}\begin{array}{c|c}t&0\rightarrow\frac{\pi}{2}\\\hline x&0\rightarrow1\end{array}$

$S_2$ の区間は

$\def\arraystretch{1.5}\begin{array}{c|c}t&\frac{\pi}{2}\rightarrow\pi\\\hline x&1\rightarrow0\end{array}$

ここで注意が必要です。$S_2$ の積分区間が 1 から 0 となり，積分するとマイナスの値になってしまいます。

簡単な例で言えば

$\displaystyle\int_0^1 2x\space dx=\Big[x^2\Big]_0^1=1-0=1$
$\displaystyle\int_1^0 2x\space dx=\Big[x^2\Big]_1^0=0-1=-1$

という感じです。ふだん，積分で図形の面積を求めるときは，ヨコ方向をなんとなく左から右で式を作ってしまうのでこういったことを意識することはありません。

ただし，媒介変数の場合は $t$ が増えるときに $x$ は減少することがあるので，注意が必要です。

結局 $S_2$ は負の値なので

$\displaystyle S=\int_0^\frac{\pi}{2} (1+\cos t)\sin t\space dx\textcolor{red}{+}\int_\frac{\pi}{2}^\pi (1+\cos t)\sin t\space dx$

が正解です。

こうすると，2 つの積分を 1 つにまとめることができます。

$\displaystyle=\int_0^\pi (1+\cos t)\sin t\space dx$

置換すると

$\displaystyle=\int_0^\pi (1+\cos t)\sin t\cos t\space dt$
$\displaystyle=\int_0^\pi \sin t\cos t+\sin t\cos^2t\space dt$

2 倍角の公式 $\sin 2x=2\sin x\cos x$ より

$\displaystyle=\int_0^\pi\cfrac{1}{2}(2\sin t\cos t)+\sin t\cos^2 t\space dt$
$\displaystyle=\int_0^\pi\cfrac{1}{2}\sin 2t+\sin t\cos^2 t\space dt$

ここで，$(\cos^3t)’=3\cos^2t\cdot(-\sin t)$ となることを利用して積分します。

$=\Big[-\cfrac{1}{4}\cos 2t-\cfrac{1}{3}\cos^3t\Big]_0^\pi$
$=-\cfrac{1}{4}\cdot1-\cfrac{1}{3}\cdot(-1)^3-\Big(-\cfrac{1}{4}-\cfrac{1}{3}\Big)$
$=-\cfrac{1}{4}+\cfrac{1}{3}+\cfrac{1}{4}+\cfrac{1}{3}$
$=\cfrac{2}{3}$　（答え）