ベクトルと三角形の重心の性質/三角形の角を始点にするならどう表す?(神戸大理系第2問・文系第3問)
$|\overrightarrow{\text{AB}}|=2$ をみたす △PAB を考え,辺 AB の中点を M,△PAB の重心を G とする。以下の問に答えよ。
(1) $|\overrightarrow{\text{PM}}|^2$ を内積 $\overrightarrow{\text{PA}}\cdot\overrightarrow{\text{PB}}$ を用いて表わせ。
(2) $\angle\text{AGB}=\cfrac{\pi}{2}$ のとき,$\overrightarrow{\text{PA}}\cdot\overrightarrow{\text{PB}}$ の値を求めよ。
(3) 点 A と点 B を固定し,$\overrightarrow{\text{PA}}\cdot\overrightarrow{\text{PB}}=\cfrac{5}{4}$ をみたすように点 P を動かすとき,$\angle\text{ABG}$ の最大値を求めよ。ただし,$0<\angle\text{ABG}<\pi$ とする。
式を二乗して内積を取り出す

(1)から始めます。
$\overrightarrow{\text{PM}}=\cfrac{1}{2}(\overrightarrow{\text{PA}}+\overrightarrow{\text{PB}})$
両辺を二乗します。
$|\overrightarrow{\text{PM}}|^2=\cfrac{1}{4}(\overrightarrow{\text{PA}}+\overrightarrow{\text{PB}})^2$
$=\cfrac{1}{4}(|\overrightarrow{\text{PA}}|^2+2\overrightarrow{\text{PA}}\cdot\overrightarrow{\text{PB}}+|\overrightarrow{\text{PB}}|^2)$ ・・・①
ここで,$|\overrightarrow{\text{AB}}|=2$ を利用して $|\overrightarrow{\text{PA}}|$ と $|\overrightarrow{\text{PB}}|$ を求めてみます。
$\overrightarrow{\text{AB}}=\overrightarrow{\text{PB}}-\overrightarrow{\text{PA}}$ より
$|\overrightarrow{\text{AB}}|^2=(\overrightarrow{\text{PB}}-\overrightarrow{\text{PA}})^2$
$2^2=|\overrightarrow{\text{PB}}|^2-2\overrightarrow{\text{PA}}\cdot\overrightarrow{\text{PB}}+|\overrightarrow{\text{PA}}|^2$
$|\overrightarrow{\text{PA}}|^2+|\overrightarrow{\text{PB}}|^2=4+2\overrightarrow{\text{PA}}\cdot\overrightarrow{\text{PB}}$
①に代入すると
$|\overrightarrow{\text{PM}}|^2=\cfrac{1}{4}(4+4\overrightarrow{\text{PA}}\cdot\overrightarrow{\text{PB}})$
$=1+\overrightarrow{\text{PA}}\cdot\overrightarrow{\text{PB}}$ (答え)
内積0を利用する
(2)に進みます。ここは実は円周角の定理をうまく使うと速く解けます。とは言え,ここではそれがひらめかなかったら,という前提で話を進めます。
$\angle\text{AGB}=\cfrac{\pi}{2}$ より,$\overrightarrow{\text{GA}}\cdot\overrightarrow{\text{GB}}=0$ が成り立ちます。
求めたいのは $\overrightarrow{\text{PA}}\cdot\overrightarrow{\text{PB}}$ なので,点 P をスタート地点にして式を書いてみましょう。
$\overrightarrow{\text{GA}}\cdot\overrightarrow{\text{GB}}=(\overrightarrow{\text{PA}}-\overrightarrow{\text{PG}})(\overrightarrow{\text{PB}}-\overrightarrow{\text{PG}})=0$ ・・・②
こうなると,$\overrightarrow{\text{PG}}$ を求めないと先に進めそうにありません。
点 G は三角形の重心だから,原点 O を始点するなら
$\overrightarrow{\text{OG}}=\cfrac{1}{3}(\overrightarrow{\text{OP}}+\overrightarrow{\text{OA}}+\overrightarrow{\text{OB}})$
と表すことができます。


$\overrightarrow{\text{PG}}=\cfrac{1}{3}(\overrightarrow{\text{PP}}+\overrightarrow{\text{PA}}+\overrightarrow{\text{PB}})$

$\overrightarrow{\text{PG}}=\cfrac{1}{3}(\overrightarrow{\text{PA}}+\overrightarrow{\text{PB}})$
②に代入して
$\Big\{\overrightarrow{\text{PA}}-\cfrac{1}{3}(\overrightarrow{\text{PA}}+\overrightarrow{\text{PB}})\Big\}\Big\{\overrightarrow{\text{PB}}-\cfrac{1}{3}(\overrightarrow{\text{PA}}+\overrightarrow{\text{PB}})\Big\}=0$
$\Big(\cfrac{2}{3}\overrightarrow{\text{PA}}-\cfrac{1}{3}\overrightarrow{\text{PB}}\Big)\Big(\cfrac{2}{3}\overrightarrow{\text{PB}}-\cfrac{1}{3}\overrightarrow{\text{PA}}\Big)=0$
$(2\overrightarrow{\text{PA}}-\overrightarrow{\text{PB}})(2\overrightarrow{\text{PB}}-\overrightarrow{\text{PA}})=0$
$4\overrightarrow{\text{PA}}\cdot\overrightarrow{\text{PB}}-2|\overrightarrow{\text{PA}}|^2-2|\overrightarrow{\text{PB}}|^2+\overrightarrow{\text{PA}}\cdot\overrightarrow{\text{PB}}=0$
$5\overrightarrow{\text{PA}}\cdot\overrightarrow{\text{PB}}=2(|\overrightarrow{\text{PA}}|^2+|\overrightarrow{\text{PB}}|^2)$
(1)で,$|\overrightarrow{\text{PA}}|^2+|\overrightarrow{\text{PB}}|^2=4+2\overrightarrow{\text{PA}}\cdot\overrightarrow{\text{PB}}$ だったので
$5\overrightarrow{\text{PA}}\cdot\overrightarrow{\text{PB}}=8+4\overrightarrow{\text{PA}}\cdot\overrightarrow{\text{PB}}$
$\overrightarrow{\text{PA}}\cdot\overrightarrow{\text{PB}}=8$ (答え)
角の最大値
(3)に進みます。
$\overrightarrow{\text{PA}}\cdot\overrightarrow{\text{PB}}=\cfrac{5}{4}$ のとき,(1)より
$|\overrightarrow{\text{PM}}|^2=1+\cfrac{5}{4}=\cfrac{9}{4}$
$|\overrightarrow{\text{PM}}|=\cfrac{3}{2}$
が成り立ちます。
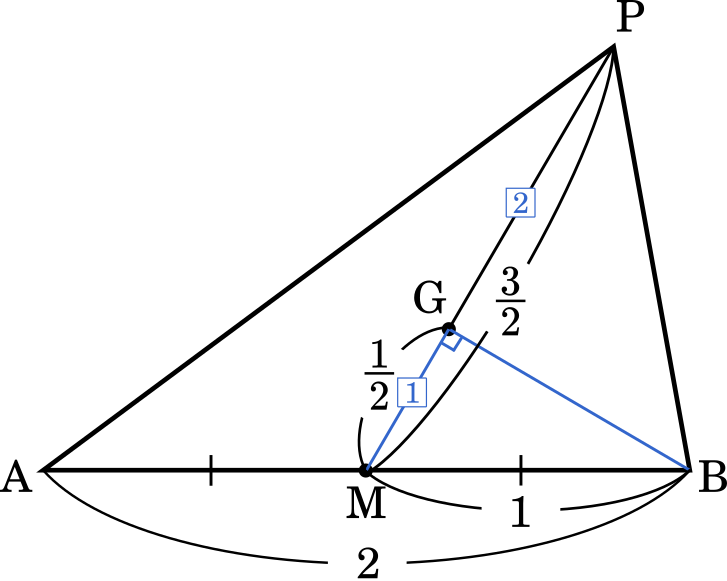
三角形の重心の性質から,PG : GM = 2 : 1 が成り立ちます。よって
$\text{GM}=\cfrac{1}{2}$
ここから,$\angle\text{ABG}$ の最大値を考えてみましょう。
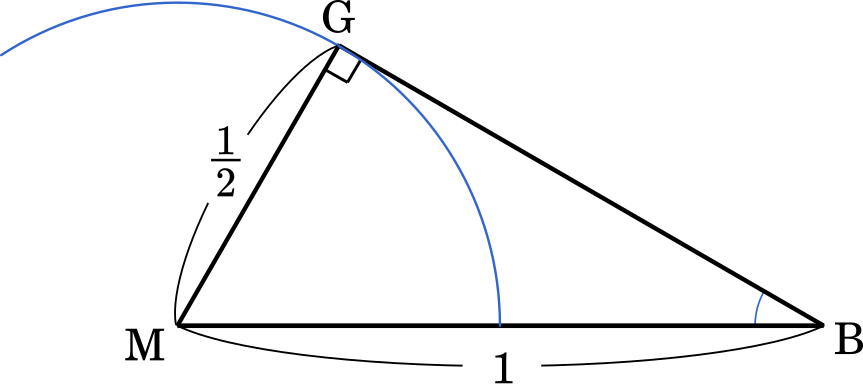
点 G が点 A を中心とする円周上を動くとすると,$\angle\text{AGB}=90\degree$ のときに $\angle\text{ABG}$ は最大となります。
このとき,△ABGは辺の比が $1:2:\sqrt{3}$ の直角三角形になるので,$\angle\text{ABG}$ は
$\cfrac{\pi}{6}$ (答え)
SNSでシェア