log x/x の最大値の求め方／e^x と x^a の大小関係を求める（神戸大2019理系第1問）

以下の問に答えよ。

(1) 関数

$f(x)=\cfrac{\log x}{x}$

の $x>0$ における最大値とそのときの $x$ の値を求めよ。

(2) $a$ を $a\not=1$ をみたす正の実数とする。曲線 $y=e^x$ と曲線 $y=x^a$ $(x>0)$ が共有点 P をもち，さらに点 P において共通の接線をもつとする。点 P の $x$ 座標を $t$ とするとき，$a$ と $t$ の値を求めよ。

(3) $a$ と $t$ を(2)で求めた実数とする。$x$ を $x\not=t$ をみたす正の実数とするとき，$e^x$ と $x^a$ の大小を判定せよ。

微分して増減表をつくる

(1)から始めます。

$f'(x)=\cfrac{\cfrac{1}{x}\cdot x-\log x}{x^2}$
$=\cfrac{1-\log x}{x^2}$

$\cfrac{1-\log x}{x^2}=0$ とすると

$x\not=0$ より
$1-\log x=0$
$\log x=1$

$x=e$

増減表は

$\def\arraystretch{1.5}\begin{array}{|c||c|c|c|c|}\hline x&(0)&\cdots&e&\cdots\\\hline f'(x)&&+&0&-\\\hline f(x)&&\nearrow&\frac{1}{e}&\searrow\\\hline\end{array}$

$f(e)=\cfrac{\log e}{e}=\cfrac{1}{e}$

最大値は $x=e$ のとき $\cfrac{1}{e}$　（答え）

x^a と x^a の共通の接線

(2)に進みます。

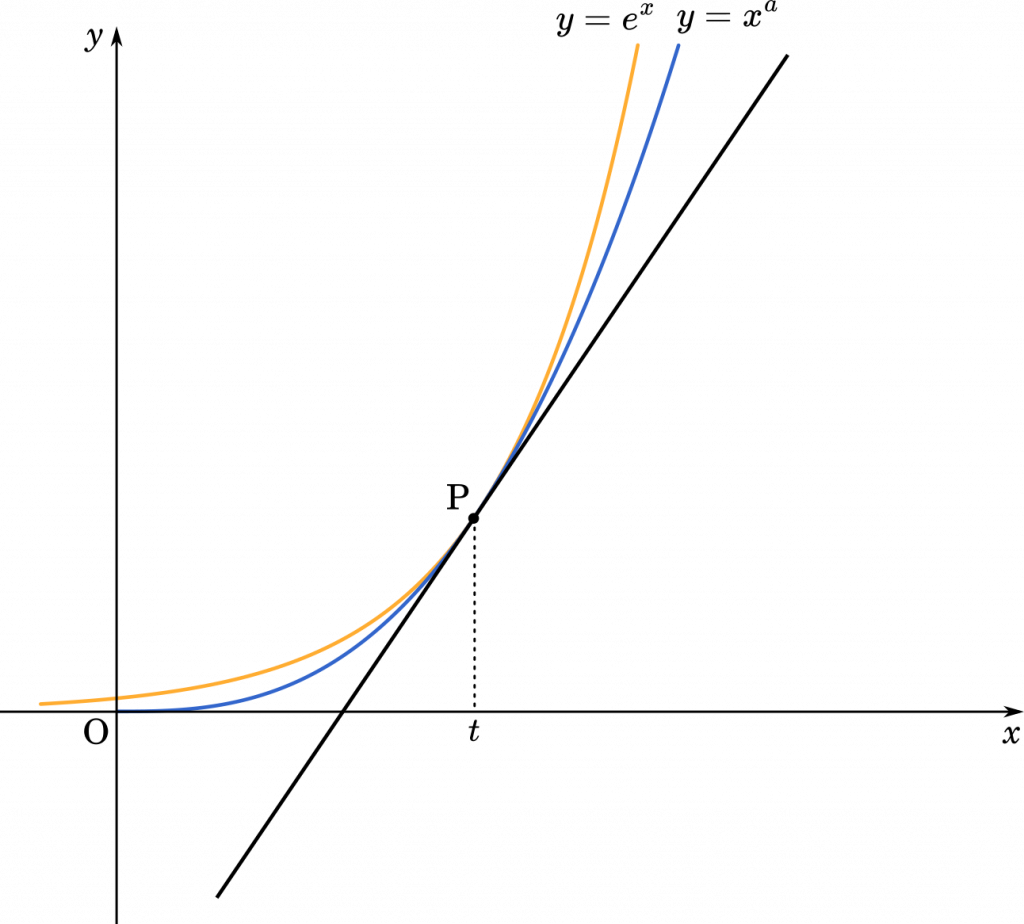
まず，それぞれの関数について接線の傾きを考えてみましょう。

$y=e^x$ とすると

$y’=e^x$

また

$y=x^a$ とすると

$y’=ax^{a-1}$

$x=t$ のとき，それぞれの接線の傾きが一致するので

$e^t=at^{a-1}$　・・・①

また，$x=t$ のとき，$y$ 座標が一致するので

$e^t=t^a$　・・・②

$at^{a-1}=t^a$
$at^{-1}=1$
$a=t$

②に代入して

$e^a=t^a$
$e=t$

したがって

$(a,e)=(e,e)$　（答え）

e^aとx^aの大小関係

(3)に進みます。

大小関係を考えるには，式どうしを引き算して正の数になるか負の数になるかを調べます。

$y=e^x$

$y=x^e$

($x\not=e$)

とは言え，このまま引き算をして $e^x-x^e$ という式を作っても正の数なのか負の数なのかはわかりません。

そこで，それぞれの対数をとった上で引き算してみます。

$g(x)=\log e^x-\log x^e$ とする

$g(x)=x-e\log x$

微分すると

$g'(x)=1-\cfrac{e}{x}$

$1-\cfrac{e}{x}=0$ とすると

$1=\cfrac{e}{x}$
$x=e$

増減表は

$\def\arraystretch{1.5}\begin{array}{|c||c|c|c|c|}\hline x&(0)&\cdots&(e)&\cdots\\\hline g'(x)&&-&(0)&+\\\hline g(x)&&\searrow&(0)&\nearrow\\\hline\end{array}$

したがって，$e^x>x^a$　（答え）