ベクトル内積の最小値を求める(東京都立大2020理学部第2問)

O を原点とする座標平面の $x$ 軸上に点 A があり，第1象限に点 B がある。A の $x$ 座標は正であるとし，∠OAB＝$\cfrac{\pi}{3}$，∠AOB＝$\cfrac{\pi}{4}$，AB ＝ 2 とする。原点 O から直線 AB に下ろしたセ垂線を OC とし，点 B から直線 OA に下ろした垂線を BD とする。以下の問いに答えなさい。（東京都立大2020）

(1) 線分 OA，OB の長さを求めなさい。

(2) 点 C の座標を求めなさい。

(3) 実数 $t$ は $0<t<1$ の範囲を動くとする。線分 AB を $t:(1-t)$ に内分する点を $\text{P}_t$ とし，線分 CD を $(1-t):t$ に内分する点を $\text{Q}_t$ とする。内積 $\overrightarrow{\text{OP}_t}\cdot\overrightarrow{\text{OQ}_t}$ の最小値を求めなさい。また，そのときの $t$ の値を求めなさい。

三角比から辺の長さを求める

(1)から始めます。

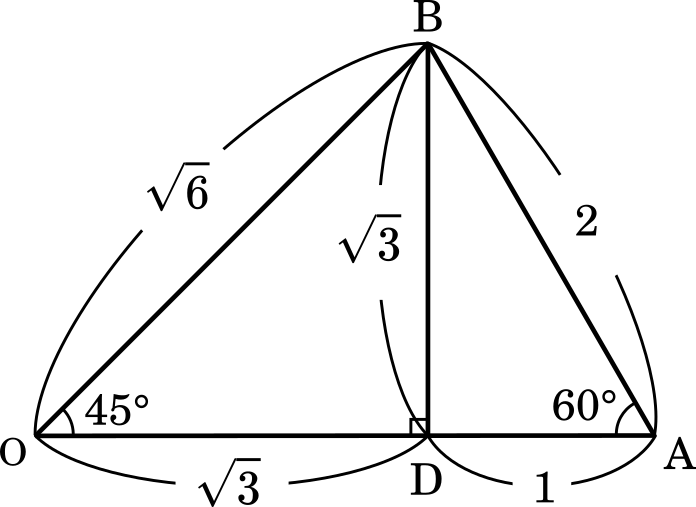
ここは計算式を立てるより，辺の比が $1:2:\sqrt{3}$ と $1:1:\sqrt{2}$ の直角三角形を作った方が話が早いでしょう。
上の図より

OA＝$1+\sqrt{3}$
OB＝$\sqrt{6}$　（答え）

さらに三角比を用いる

(2)に進みます。

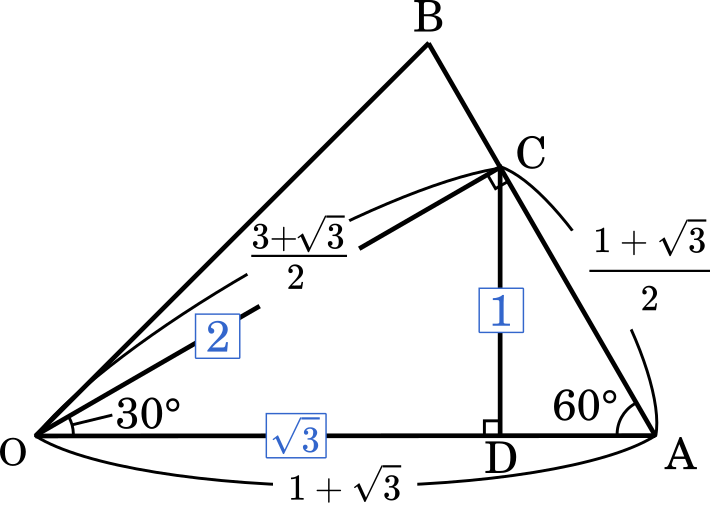
これも(1)と同じで，△OAC は辺の比が $1:2:\sqrt{3}$ の直角三角形になることを利用した方が良いでしょう。OA の長さが $1+\sqrt{3}$ であることから，他の 2 つの辺の長さもすぐに求められます。

OA＝$1+\sqrt{3}$ より

OA：OC＝$2:\sqrt{3}$

OC＝$\cfrac{\sqrt{3}}{2}$ OA
$=\cfrac{\sqrt{3}}{2}(1+\sqrt{3})$
$=\cfrac{3+\sqrt{3}}{2}$

よって

OC：CD＝$2:1$
CD＝$\cfrac{1}{2}$ OC
$=\cfrac{1}{2}\cdot\cfrac{3+\sqrt{3}}{2}$
$=\cfrac{3+\sqrt{3}}{4}$

また

OC：OD＝$2:\sqrt{3}$
OD＝$\cfrac{\sqrt{3}}{2}$ OC
$=\cfrac{\sqrt{3}}{2}\cdot\cfrac{3+\sqrt{3}}{2}$
$=\cfrac{3+3\sqrt{3}}{4}$

したがって，点 C の座標は

$\Big(\cfrac{3+3\sqrt{3}}{4},\cfrac{3+\sqrt{3}}{4}\Big)$　（答え）

平方完成して最小値を求める

(3)に進みます。

ここは内分点を求め，そこから内積を求めます。作業は難しくないので，地道に計算式を作っていきましょう。

内分点の式は

$\overrightarrow{\text{OP}_t}=(1-t)\overrightarrow{\text{OA}}+t\overrightarrow{\text{OB}}$
$\overrightarrow{\text{OQ}_t}=t\overrightarrow{\text{OC}}+(1-t)\overrightarrow{\text{OD}}$

内積の式は

$\overrightarrow{\text{OP}_t}\cdot\overrightarrow{\text{OQ}_t}=\{(1-t)\overrightarrow{\text{OA}}+t\overrightarrow{\text{OB}}\}\{t\overrightarrow{\text{OC}}+(1-t)\overrightarrow{\text{OD}}\}$
$=(t-t^2)\overrightarrow{\text{OA}}\cdot\overrightarrow{\text{OC}}+(1-t)^2\overrightarrow{\text{OA}}\cdot\overrightarrow{\text{OD}}+t^2\overrightarrow{\text{OB}}\cdot\overrightarrow{\text{OC}}+(t-t^2)\overrightarrow{\text{OB}}\cdot\overrightarrow{\text{OD}}$　・・・①

$\overrightarrow{\text{OA}}=(1+\sqrt{3},0)$
$\overrightarrow{\text{OB}}=(\sqrt{3},\sqrt{3})$
$\overrightarrow{\text{OC}}=\Big(\cfrac{3+\sqrt{3}}{4},\cfrac{3+\sqrt{3}}{4}\Big)$
$\overrightarrow{\text{OD}}=(\sqrt{3},0)$

よって

$\overrightarrow{\text{OA}}\cdot\overrightarrow{\text{OC}}=(1+\sqrt{3})\cdot\cfrac{3+3\sqrt{3}}{4}+\sqrt{3}\cdot\cfrac{3+\sqrt{3}}{4}$
$=\cfrac{1}{4}(3\sqrt{3}+9+3\sqrt{3}+3)$
$=\cfrac{1}{4}(12+6\sqrt{3})$
$=3+\cfrac{3\sqrt{3}}{2}$
$\overrightarrow{\text{OA}}\cdot\overrightarrow{\text{OD}}=\sqrt{3}(1+\sqrt{3})=3+\sqrt{3}$
$\overrightarrow{\text{OB}}\cdot\overrightarrow{\text{OC}}=\sqrt{3}\cdot\cfrac{3+3\sqrt{3}}{4}+\sqrt{3}\cdot\cfrac{3+\sqrt{3}}{4}$
$=\cfrac{1}{4}(3\sqrt{3}+9+3\sqrt{3}+3)$
$=\cfrac{1}{4}(12+6\sqrt{3})=3+\cfrac{3\sqrt{3}}{2}$
$\overrightarrow{\text{OB}}\cdot\overrightarrow{\text{OD}}=\sqrt{3}\cdot\sqrt{3}=3$

①に代入すると

$\overrightarrow{\text{OP}_t}\cdot\overrightarrow{\text{OQ}_t}=(t-t^2)\Big(3+\cfrac{3\sqrt{3}}{2}\Big)+(1-2t+t^2)(3+\sqrt{3})+t^2\Big(3+\cfrac{3\sqrt{3}}{2}\Big)+(t-t^2)\cdot3$
$=3t+\cfrac{3\sqrt{3}}{2}t-3t^2-\cfrac{3\sqrt{3}}{2}t^2+3-6t+3t^2+\sqrt{3}-2\sqrt{3}t+\sqrt{3}t^2+3t^2+\cfrac{3\sqrt{3}}{2}t^2+3t-3t^2$
$=\sqrt{3}t^2-\cfrac{\sqrt{3}}{2}t+3+\sqrt{3}$

最小値を求めるために，式を平方完成します。

$=\sqrt{3}\Big(t^2-\cfrac{1}{2}t\Big)+3+\sqrt{3}$
$=\sqrt{3}\Big(t-\cfrac{1}{4}\Big)^2-\cfrac{\sqrt{3}}{16}+3+\sqrt{3}$
$=\sqrt{3}\Big(t-\cfrac{1}{4}\Big)^2+3+\cfrac{15\sqrt{3}}{16}$

したがって

最小値は $t=\cfrac{1}{4}$ のとき $3+\cfrac{15\sqrt{3}}{16}$　（答え）