2つの円に接する円の半径(東京都立大2020理系第2問)

円 $A$ と円 $B$ と直線 $l$ がそれぞれ異なる点で接しているとする。$A$ と $l$ の接点を $\text{P}_A$ とし，$B$ と $l$ の接点を $\text{P}_B$ とする。$C_1$ を $A$ と $B$ と $l$ に接する円とする。ただし，$C_1$ と $l$ の接点 $\text{P}_1$ は，線分 $\text{P}_A\text{P}_B$ 上にあるとする。また，$C_2$ を $A$ と $C_1$ と $l$ に接する円とする。ただし，$C_2$ と $l$ の接点 $\text{P}_2$ は，線分 $\text{P}_A\text{P}_1$ 上にあるとする。以下同様に，自然数 $n$ に対し，$C_{n+1}$ は $A$ と $C_n$ と $l$ に接する円である。$C_{n+1}$ と $l$ の接点 $P_{n+1}$ は線分 $\text{P}_A\text{P}_n$ 上にあるとする。$A$ の半径を $a$ とし，$B$ の半径を $b$ とするとき，以下の問いに答えなさい。

(1) 線分 $\text{P}_A\text{P}_B$ の長さを $a,b$ を用いて表しなさい。

(2) $C_1$ の半径を $r_1$ とするとき，$\cfrac{1}{\sqrt{r_1}}$ を $a,b$ を用いて表しなさい。

(3) $C_n$ の半径を $r_n$ とするとき，$\cfrac{1}{\sqrt{r_n}}$ を $a,b,n$ を用いて表しなさい。

(4) $a$ と $b$ が $a+b=1$ をみたしながら動くとき，$C_n$ の半径 $r_n$ の最大値を $n$ を用いて表しなさい。また，そのときの $a$ の値を $n$ を用いて表しなさい。

三平方の定理を用いる

(1)から始めます。

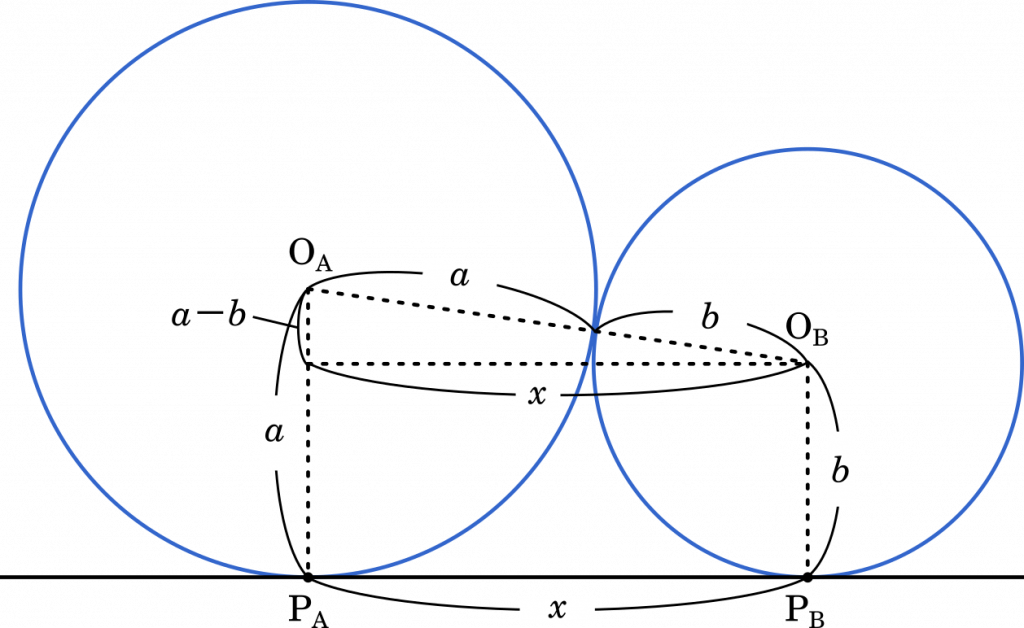
上の図のように三角形をつくって，三平方の定理から長さを求めます。

$\text{P}_A\text{P}_B=x$ とすると

三平方の定理より

$x^2+(a-b)^2=(a+b)^2$
$x^2=(a+b)^2-(a-b)^2$
$=a^2+2ab+b^2-(a^2-2ab+b^2)$
$=4ab$

$x$ は辺の長さだから，負の値になることはありません。

$x>0$ より

$x=2\sqrt{ab}$　（答え）

さらに三平方の定理を用いる

(2)に進みます。

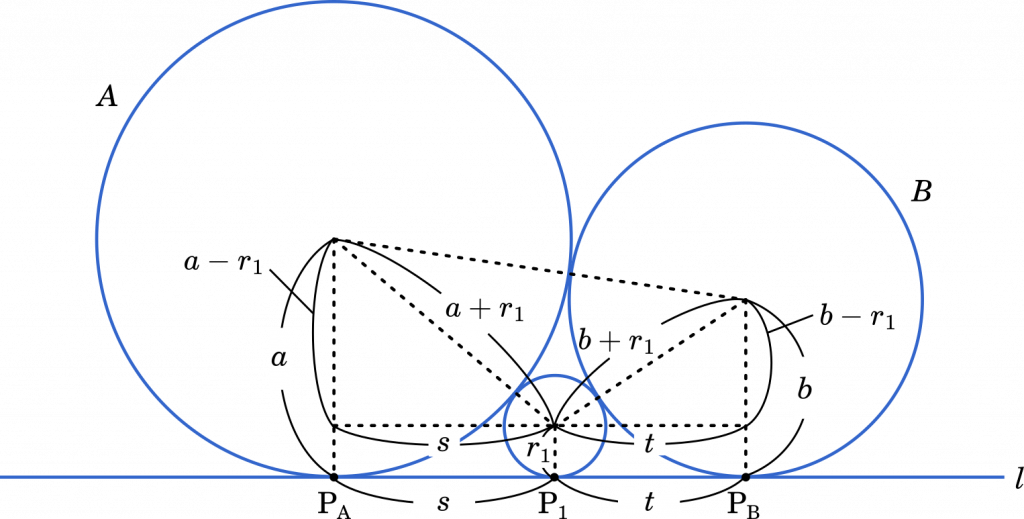
$\text{P}_A\text{P}_1=s$，$\text{P}_B\text{P}_1=t$ とすると，(1)より

$s+t=2\sqrt{ab}$

三平方の定理より

$s^2+(a-r_1)^2=(a+r_1)^2$

(1)と同じ手順で計算していきましょう。

$s=2\sqrt{ar_1}$　・・・①

また

$t^2+(b-r_1)^2=(b+r_1)^2$
$t=2\sqrt{br_1}$　・・・②

①＋②

$s+t=2\sqrt{ar_1}+2\sqrt{br_1}$
$2\sqrt{ab}=2\sqrt{ar_1}+2\sqrt{br_1}$
$\sqrt{ab}=\sqrt{r_1}(\sqrt{a}+\sqrt{b})$
$\cfrac{1}{\sqrt{r_1}}=\cfrac{\sqrt{a}+\sqrt{b}}{\sqrt{ab}}$
$=\cfrac{\sqrt{a}}{\sqrt{ab}}+\cfrac{\sqrt{b}}{\sqrt{ab}}$
$=\cfrac{1}{\sqrt{b}}+\cfrac{1}{\sqrt{a}}$

ここは，$a,b$ の順に項を並べかえたほうが良いでしょう。

$=\cfrac{1}{\sqrt{a}}+\cfrac{1}{\sqrt{b}}$ （答え）

漸化式の利用

(3)に進みます。

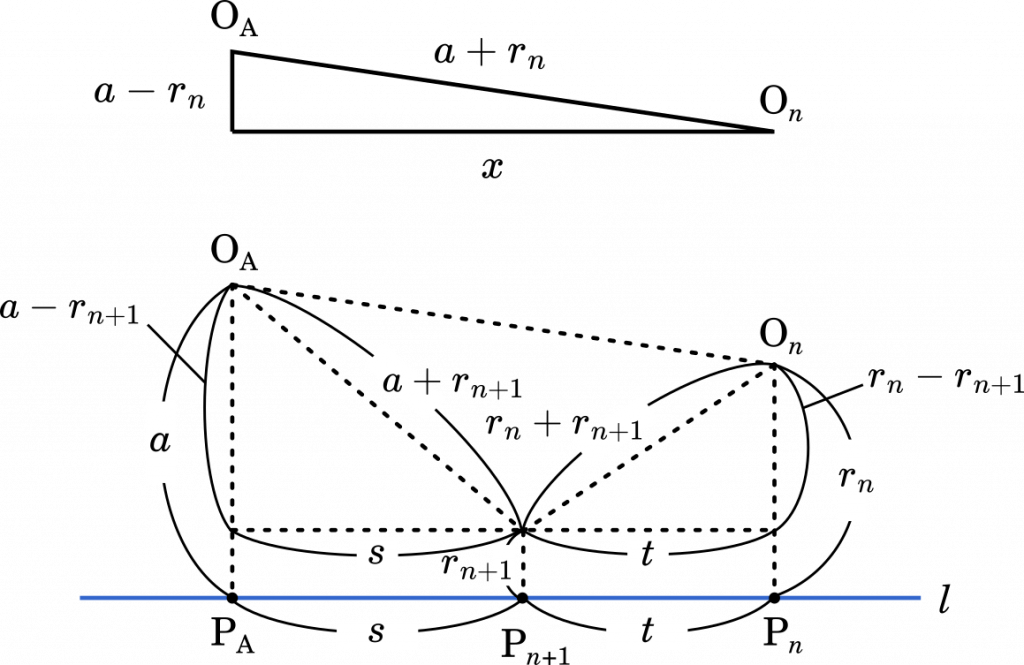
(1)と(2)でやったことをさらに進めていきます。

$\text{P}_A$ と $\text{P}_n$ の間に $\text{P}_{n+1}$ をおいて，$r_n$ と $r_{n+1}$ について考えていきます。

$\text{P}_A\text{P}_n=x$ として

三平方の定理より

$x^2+(a-r_n)^2=(a+r_n)^2$

$x=2\sqrt{ar_n}$

$\text{P}_A\text{P}_{n+1}=s$，$\text{P}_n\text{P}_{n+1}=t$ として

三平方の定理より

$s^2+(a-r_{n+1})^2=(a+r_{n+1})^2$
$s=2\sqrt{ar_{n+1}}$　・・・③

また

$t^2+(r_n-r_{n+1})^2=(r_n+r_{n+1})^2$
$t=2\sqrt{r_nr_{n+1}}$　・・・④

③＋④

$s+t=2\sqrt{r_{n+1}}(\sqrt{a}+\sqrt{r_n})$
$2\sqrt{ar_n}=2\sqrt{r_{n+1}}(\sqrt{a}+\sqrt{r_n})$
$\sqrt{ar_n}=\sqrt{r_{n+1}}(\sqrt{a}+\sqrt{r_n})$
$\sqrt{r_{n+1}}=\cfrac{\sqrt{ar_n}}{\sqrt{a}+\sqrt{r_n}}$

これで漸化式ができましたが，問題文からして逆数をとったほうが良さそうです。

$\cfrac{1}{\sqrt{r_{n+1}}}=\cfrac{\sqrt{a}+\sqrt{r_n}}{\sqrt{ar_n}}$
$=\cfrac{1}{\sqrt{r_n}}+\cfrac{1}{\sqrt{a}}$

これは，たとえば $\cfrac{1}{\sqrt{r_1}}$ に $\cfrac{1}{\sqrt{a}}$ を足すと $\cfrac{1}{\sqrt{r_2}}$ になるというだから，初項 $\cfrac{1}{\sqrt{r_1}}$，公差 $\cfrac{1}{\sqrt{a}}$ の等差数列ということになります。

初項 $a$，公差 $d$ の等比数列の一般項は

$a+(n-1)d$

よって

$\cfrac{1}{\sqrt{r_n}}=\cfrac{1}{\sqrt{r_1}}+(n-1)\cfrac{1}{\sqrt{a}}$

(2)より

$\cfrac{1}{\sqrt{r_n}}=\cfrac{1}{\sqrt{a}}+\cfrac{1}{\sqrt{b}}+(n-1)\cfrac{1}{\sqrt{a}}$
$=\cfrac{1}{\sqrt{a}}+\cfrac{1}{\sqrt{b}}+\cfrac{n}{\sqrt{a}}-\cfrac{1}{\sqrt{a}}$
$=\cfrac{n}{\sqrt{a}}+\cfrac{1}{\sqrt{b}}$ （答え）

微分して極値を求める

(4)に進みます。

$r_n$ の最大値を求めることと，$\cfrac{1}{\sqrt{r_n}}$ の最小値を求めることは同じです。

関数の最小値を求めるときは，平方完成や相加相乗平均をまず考えます。しかし，それらが使えそうにないときは微分することになります。

$f(a)=\cfrac{n}{\sqrt{a}}+\cfrac{1}{\sqrt{b}}$ $(a+b=1)$ として

$a$ で微分するなら，$a$ が含まれない項である $\cfrac{1}{\sqrt{b}}$ を微分したら，0 になると思うかもしれません。しかし，実際は $a+b=1$ より $b=1-a$ だから，$\cfrac{1}{\sqrt{b}}$ は $a$ の関数である，と考えなければなりません。これを合成関数といいます。

式を　$f(a)=\cfrac{n}{\sqrt{a}}+\cfrac{1}{\sqrt{1-a}}$　として微分します。

$f(a)=na^{\small{-\frac{1}{2}}}+(1-a)^{\small{-\frac{1}{2}}}$
$f'(a)=-\cfrac{n}{2}a^{\small{-\frac{3}{2}}}-\cfrac{1}{2}(1-a)^{\small{-\frac{3}{2}}}(-1)$

$f'(a)=-\cfrac{n}{2}a^{\small{-\frac{3}{2}}}+\cfrac{1}{2}(1-a)^{\small{-\frac{3}{2}}}$
$=\cfrac{1}{2(1-a)^{\small{\frac{3}{2}}}}-\cfrac{n}{2a^{\small{\frac{3}{2}}}}$
$=\cfrac{a^{\small{\frac{3}{2}}}-n(1-a)^{\small{\frac{3}{2}}}}{2\{a(1-a)\}^{\small{\frac{3}{2}}}}$

$f'(a)=0$ として

$\cfrac{a^{\small{\frac{3}{2}}}-n(1-a)^{\small{\frac{3}{2}}}}{2\{a(1-a)\}^{\small{\frac{3}{2}}}}=0$　($a(1-a)\ne0$)

問題文に明記されていなくても，その趣旨から言えば $a$ が 0 になる（円$A$が存在しない）ということはありえません。よって，$a$ の範囲は $0<a<1$ です。

この範囲で分母が 0 になることはないので，あとは分子が 0 になる場合を考えればよいことになります。

$a^{\small{\frac{3}{2}}}-n(1-a)^{\small{\frac{3}{2}}}=0$

$a^{\small{\frac{3}{2}}}=n(1-a)^{\small{\frac{3}{2}}}$

両辺をそれぞれ $\cfrac{2}{3}$ 乗します

$a^{\small{\frac{3}{2}\times\frac{2}{3}}}=\{n(1-a)^{\small{\frac{3}{2}}}\}^{\small{\frac{2}{3}}}$
$a=n^{\small{\frac{2}{3}}}(1-a)$

ここからは，試行錯誤が必要です。スマートな道順で解くのはなかなか難しいので，何度か失敗しながら突破口を見つけていきましょう。ここで示す解き方も，あくまで解き方の例の一つです。

$\cfrac{a}{1-a}=n^{\small{\frac{2}{3}}}$

両辺の逆数をとって

$\cfrac{1-a}{a}=\cfrac{1}{n^{\small{\frac{2}{3}}}}$
$\cfrac{1}{a}-1=\cfrac{1}{n^{\small{\frac{2}{3}}}}$
$\cfrac{1}{a}=\cfrac{1}{n^{\small{\frac{2}{3}}}}+1$
$=\cfrac{1+n^{\small{\frac{2}{3}}}}{n^{\small{\frac{2}{3}}}}$

よって

$a=\cfrac{n^{\small{\frac{2}{3}}}}{1+n^{\small{\frac{2}{3}}}}$

増減表は

$\def\arraystretch{1.5}\begin{array}{|c|c|c|c|c|c|}\hline a&(0)&\cdots&\cfrac{n^{\small{\frac{2}{3}}}}{1+n^{\small{\frac{2}{3}}}}&\cdots&(1)\\\hline f'(a)&&-&0&+\\\hline f(a)&&\searrow&&\nearrow\\\hline\end{array}$

$f'(a)=\cfrac{a^{\small{\frac{3}{2}}}-n(1-a)^{\small{\frac{3}{2}}}}{2\{a(1-a)\}^{\small{\frac{3}{2}}}}$

から考えると，分母はつねに正の値です。次に分子を考えましょう。

$a$ の値が 0 に近づくと，$a^{\small{\frac{3}{2}}}$ は 0 に近づき，$(1-a)^{\small{\frac{3}{2}}}$ は 1 に近づきます。$n$ は 1 以上の正の数だから，全体として負の数になるはずです。

$a$ の値が 1 に近づいた場合はどうでしょうか。$a^{\small{\frac{3}{2}}}$ は 1 に近づき，$(1-a)^{\small{\frac{3}{2}}}$ は 0 に近づきます。$n$ は 1 以上の正の数だから，全体として正の数になるはずです。

これで $\cfrac{1}{\sqrt{r_n}}$ が最小値をとるときの $a$ の値が分かりました。上で述べた通り，これが $r_n$ の最大となるときです。あとはここから $r_n$ を求めていきましょう。

$a=\cfrac{n^{\small{\frac{2}{3}}}}{1+n^{\small{\frac{2}{3}}}}$ より

$1-a=1-\cfrac{n^{\small{\frac{2}{3}}}}{1+n^{\small{\frac{2}{3}}}}$
$=\cfrac{1+n^{\small{\frac{2}{3}}}-n^{\small{\frac{2}{3}}}}{1+n^{\small{\frac{2}{3}}}}$
$=\cfrac{1}{1+n^{\small{\frac{2}{3}}}}$

となるので

$\cfrac{1}{\sqrt{r_n}}=\cfrac{n}{\sqrt{a}}+\cfrac{1}{\sqrt{1-a}}$
$=\cfrac{n}{\sqrt{\cfrac{n^{\small{\frac{2}{3}}}}{1+n^{\small{\frac{2}{3}}}}}}+\cfrac{1}{\sqrt{\cfrac{1}{1+n^{\small{\frac{2}{3}}}}}}$
$=\cfrac{n\sqrt{1+n^{\small{\frac{2}{3}}}}}{\sqrt{n^{\small{\frac{2}{3}}}}}+\sqrt{1+n^{\small{\frac{2}{3}}}}$

式が複雑になってきたので，部分的に整理しましょう。

$\sqrt{n^{\small{\frac{2}{3}}}}=n^{\small{\frac{2}{3}\times\frac{1}{2}}}$
$=n^{\small{\frac{1}{3}}}$

となるので

$\cfrac{n}{\sqrt{n^{\small{\frac{2}{3}}}}}=n\times n^{\small{-\frac{1}{3}}}$
$=n^{\small{\frac{2}{3}}}$

よって

$=n^{\small{\frac{2}{3}}}\sqrt{1+n^{\small{\frac{2}{3}}}}+\sqrt{1+n^{\small{\frac{2}{3}}}}$
$=(1+n^{\small{\frac{2}{3}}})\sqrt{1+n^{\small{\frac{2}{3}}}}$
$=(1+n^{\small{\frac{2}{3}}})(1+n^{\small{\frac{2}{3}}})^{\small{\frac{1}{2}}}$
$=(1+n^{\small{\frac{2}{3}}})^{\small{\frac{3}{2}}}$

両辺を 2 乗して

$\cfrac{1}{r_n}=(1+n^{\small{\frac{2}{3}}})^3$

両辺の逆数をとって

$r_n=\cfrac{1}{(1+n^{\small{\frac{2}{3}}})^3}$

よって，$r_n$ は $a=\cfrac{n^{\small{\frac{2}{3}}}}{1+n^{\small{\frac{2}{3}}}}$ のとき，最大値 $\cfrac{1}{(1+n^{\small{\frac{2}{3}}})^3}$ をとる。（答え）