三角関数の合成/最大と最小(東京都立大2019文系第2問)

$\theta$ を $0\leqq\theta\leqq 2\pi$ をみたす実数として，

$f(\theta)=\sqrt{3}\sin2\theta-\cos2\theta-2\sqrt{6}\sin\theta-2\sqrt{2}\cos\theta$

とする。$x=\sqrt{3}\sin\theta+\cos\theta$ とおく。以下の問いに答えなさい。（東京都立大2019）

(1) $x$ を $r\sin(\theta+\alpha)$ の形に表しなさい。ただし，$\alpha$ は実数，$r$ は正の実数とする。

(2) $f(\theta)$ を $x$ の式で表しなさい。

(3) $f(\theta)$ の最大値と最小値，およびそのときの $\theta$ の値を求めなさい。

三角関数の合成

(1)から始めます。$r\sin(\theta+\alpha)$ は三角関数の合成をするということです。
$x=\sqrt{3}\sin\theta+\cos\theta$ を用いて

三角関数の合成より

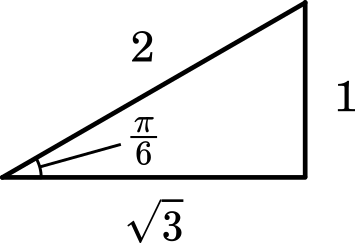
$x=2\sin\Big(\theta+\cfrac{\pi}{6}\Big)$　（答え）

２倍角の公式

(2)に進みます。

$f(\theta)=\sqrt{3}\sin2\theta-\cos2\theta-2\sqrt{6}\sin\theta-2\sqrt{2}\cos\theta$

２倍角の公式を使って，$2\theta$ の部分を整理していきましょう。

２倍角の公式より

$\sin2\theta=2\sin\theta\cos\theta$

また

$\cos2\theta=\cos^2\theta-\sin^2\theta$
$=(1-\sin^2\theta)-\sin^2\theta$
$=1-2\sin^2\theta$

これらを代入すると

$f(\theta)=2\sqrt{3}\sin\theta\cos\theta-1+2\sin^2\theta-2\sqrt{2}(\sqrt{3}\sin\theta+\cos\theta)$　・・・①

問題文より，$x=\sqrt{3}\sin\theta+\cos\theta$ でした。これを 2 乗してみましょう。

$x^2=3\sin^2\theta+2\sqrt{3}\sin\theta\cos\theta+\cos^2\theta$

$3\sin^2\theta=\sin^2\theta+2\sin^2\theta$ とすると，三角比の公式 $\sin^2\theta+\cos^2\theta=1$ より

$x^2=2\sin^2\theta+2\sqrt{3}\sin\theta\cos\theta+1$

移項して

$2\sin^2\theta+2\sqrt{3}\sin\theta\cos\theta=x^2-1$

①に代入すると

$f(\theta)=x^2-1-1-2\sqrt{2}x$
$=x^2-2\sqrt{2}x-2$　（答え）

関数の最大・最小を求める

(3)に進みます。(2)で作った $x$ の関数を用いて最大最小を考えていきます。

$f(\theta)=x^2-2\sqrt{2}x-2$

平方完成して

$=(x-\sqrt{2})^2-2-2$
$=(x-\sqrt{2})^2-4$　・・・②

これで $x=\sqrt{2}$ のときにグラフの頂点が $y=-4$ となることが分かります。次に $x$ の範囲を考えましょう。

$0\leqq\theta\leqq2\pi$ より
$\cfrac{\pi}{6}\leqq\theta+\cfrac{\pi}{6}\leqq\cfrac{13\pi}{6}$
$-1\leqq\sin\Big(\theta+\cfrac{\pi}{6}\Big)\leqq1$

$-2\leqq2\sin\Big(\theta+\cfrac{\pi}{6}\Big)\leqq2$

(1)より

$-2\leqq x\leqq2$

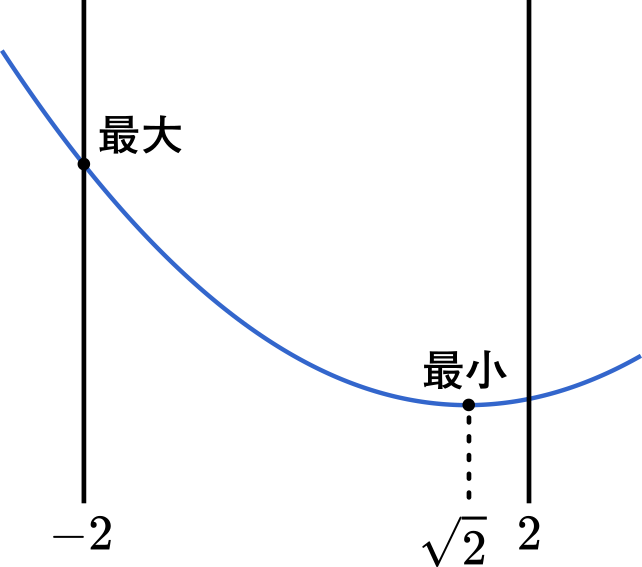
$x$ の範囲が決まると，$x=-2$ のときが最大で，$x=\sqrt{2}$ のときが最小であることが分かります。

あとは計算していきましょう。

②に $x=-2$ を代入すると

$f(-2)=(-2-\sqrt{2})^2-4$
$=4+4\sqrt{2}+2-4$
$=2+4\sqrt{2}$

さらに，$x=-2$ のときの $\theta$ の値も求めます。

$x=-2$
$2\sin\Big(\theta+\cfrac{\pi}{6}\Big)=-2$
$\sin\Big(\theta+\cfrac{\pi}{6}\Big)=-1$

上の不等式で $\cfrac{\pi}{6}\leqq\theta+\cfrac{\pi}{6}\leqq\cfrac{13\pi}{6}$ だったので，この範囲で $\sin$ の値が $-1$ となるのは，$\cfrac{3\pi}{2}$ のときだけです。

$\theta+\cfrac{\pi}{6}=\cfrac{3\pi}{2}$
$\theta=\cfrac{4\pi}{3}$

今度は最小値を求めます。

$f(\sqrt{2})=-4$

また，$x=\sqrt{2}$　のとき

$2\sin\Big(\theta+\cfrac{\pi}{6}\Big)=\sqrt{2}$
$\sin\Big(\theta+\cfrac{\pi}{6}\Big)=\cfrac{\sqrt{2}}{2}$

$\theta+\cfrac{\pi}{6}=\cfrac{\pi}{4},\space\cfrac{3\pi}{4}$
$\theta=\cfrac{\pi}{12},\space\cfrac{7\pi}{12}$

したがって

最大値は $\theta=\cfrac{4\pi}{3}$ のとき $2+4\sqrt{2}$

最小値は $\theta=\cfrac{\pi}{12},\space\cfrac{7\pi}{12}$ のとき $-4$

（答え）