【積分】6 分の 1 公式の証明のやり方(東京都立大2019文系第1問)

$a$ を実数とし，$xy$ 平面上の曲線 $y=(x-a)^2-a$ と $y=-x^2$ をそれぞれ $C_1$ と $C_2$ とする。以下の問いに答えなさい。

(1) $C_1$ と $C_2$ が 2 つの異なる交点をもつとき，$a$ のとり得る値の範囲を求めなさい。

(2) $\alpha$ と $\beta$ を実数とする。次の等式が成り立つことを示しなさい。

$\displaystyle\int_\alpha^\beta(x-\alpha)(x-\beta)dx=-\cfrac{1}{6}(\beta-\alpha)^3$

(3) $a$ は(1)で求めた範囲を動くとする。$C_1$ と $C_2$ によって囲まれた図形の面積を $S(a)$ で表わす。$S(a)$ が最大になる $a$ の値と，そのときの $S(a)$ の値を求めなさい。

式を連立する

(1)から始めます。交点を求めるので 2 つの式を連立しましょう。

$C_1:y=(x-a)^2-a$
$C_2:y=-x^2$

として，式を連立すると

$(x-a)^2-a=-x^2$
$x^2-2ax+a^2-a=-x^2$
$2x^2-2ax+a^2-a=0$

2 つの異なる交点をもつということは，この式が 2 つの異なる実数解をもつということと同じです。

$\cfrac{D}{4}=a^2-2(a^2-a)>0$
$-a^2+2a>0$
$a^2-2a<0$
$a(a-2)<0$

したがって $a$ の範囲は

$0<a<2$　（答え）

6 分の 1 公式を求める

(2)に進みます。

実際に式を変形して 6 分の 1 公式を求めてみましょう。おそらく教科書にはもう少し賢いやり方が書いてあるはずですが，ここでは計算力だけで突破してみます。

$\displaystyle\int_\alpha^\beta(x-\alpha)(x-\beta)dx$
$\displaystyle\int_\alpha^\beta x^2-(\alpha+\beta)x+\alpha\beta\space dx$
$=\Big[\cfrac{x^3}{3}-\cfrac{\alpha+\beta}{2}x^2+\alpha\beta x\Big]^\beta_\alpha$

ゴール地点を考えながら式を変形しましょう。最終的に $-\cfrac{1}{6}$ が前にでてくるハズなので，ここでその操作をします。

$=-\cfrac{1}{6}\Big[-2x^3+3(\alpha+\beta)x^2-6\alpha\beta x\Big]_\alpha^\beta$
$=-\cfrac{1}{6}\Big[-2x^3+3\alpha x^2+3\beta x^2-6\alpha\beta x\Big]_\alpha^\beta$
$=-\cfrac{1}{6}(-2\beta^3+3\alpha\beta^2+3\beta^3-6\alpha\beta^2+2\alpha^3-3\alpha^3-3\alpha^2\beta+6\alpha^2\beta)$
$=-\cfrac{1}{6}(\beta^3-3\alpha\beta^2+3\alpha^2\beta-\alpha^3)$

したがって

$=-\cfrac{1}{6}(\beta-\alpha)^3$　（証明終わり）

6 分 1 公式の応用

(3) に進みます。

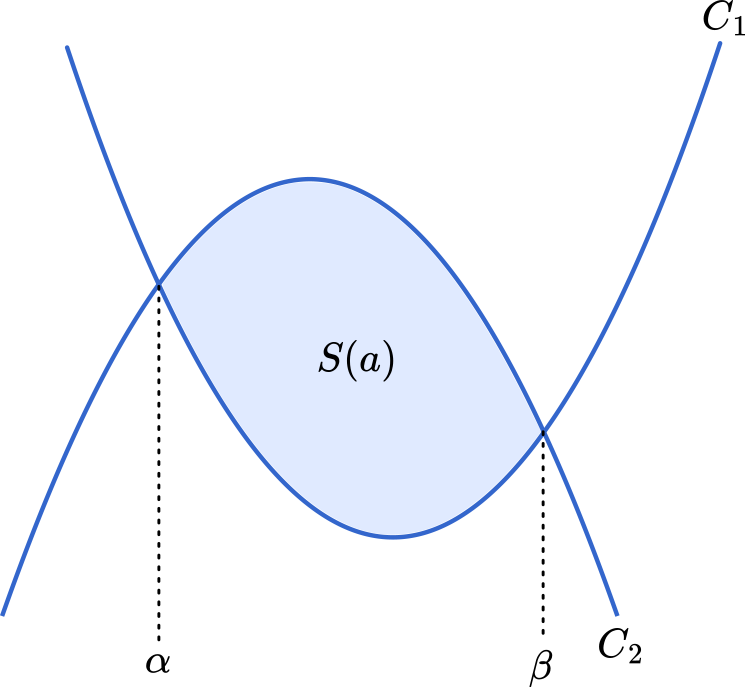
$C_1$ と $C_2$ の交点をそれぞれ $\alpha$，$\beta$ として面積を求めます。このとき，グラフ上では $C_2$ の方が $C_1$ の上になるので，$C_2$ から $C_1$ を引きます。

$\displaystyle S(a)=\int_\alpha^\beta -x^2-(x-a)^2+a\space dx$
$\displaystyle=\int_\alpha^\beta -x^2-x^2+2ax-a^2+a\space dx$
$\displaystyle=\int_\alpha^\beta -2x^2+2ax-a^2+a\space dx$

数IIで解と係数の関係などを習っていたころに，2 次式の因数分解について以下のことを習いました。

よって

$\displaystyle=\int_\alpha^\beta -2(x-\alpha)(x-\beta)\space dx$

$\displaystyle=-2\int_\alpha^\beta (x-\alpha)(x-\beta)\space dx$

(2)より

$=-2\times\Big(-\cfrac{1}{6}\Big)(\beta-\alpha)^3$
$S(a)=\cfrac{1}{3}(\beta-\alpha)^3$

$\beta-\alpha$ は正の数だから，$\beta-\alpha$ の最大を考えることで $S(a)$ の最大が求められそうです。

ここも，あれこれ考えるよりは計算力で突破してみます。

$\alpha$，$\beta$ は $C_1$ と $C_2$ の交点だから(1)で作った式が使えます。

(1)より

$2x^2-2ax+a^2-a=0$

$x=\cfrac{a\pm\sqrt{a^2-2(a^2-a)}}{2}$
$x=\cfrac{a\pm\sqrt{-a^2+2a}}{2}$
$\alpha=\cfrac{a-\sqrt{-a^2+2a}}{2}$，$\beta=\cfrac{a+\sqrt{-a^2+2a}}{2}$

よって

$\beta-\alpha=\cfrac{a+\sqrt{-a^2+2a}}{2}-\cfrac{a-\sqrt{-a^2+2a}}{2}$
$=\sqrt{-a^2+2a}$

となるので

$S(a)=\cfrac{1}{3}(\sqrt{-a^2+2a})^3$

ここで，$-a^2+2a$ の最大を求めてみましょう。

$f(a)=-a^2+2a$ として，平方完成すると

$=-(a^2-2a)$
$=-(a-1)^2+1$

よって，$-a^2+2a$ は $a=1$ のとき，最大値 1 をとります。

$S(1)=\cfrac{1}{3}(\sqrt{1})^3$
$=\cfrac{1}{3}$

したがって，$S(a)$ は $a=1$ のとき最大値 $\cfrac{1}{3}$　（答え）