正四面体を辺の中点で切ったときの体積の求め方(東京都立大2018文系第4問)

1 辺の長さが 1 である正四面体 OABC において，辺 AB の中点を M，辺 AC の中点を N とする。このとき，以下の問いに答えなさい。(東京都立大2018)

(1) 三角形 OMN の面積を求めなさい。

(2) 3 点 O，M，N が定める平面を $\alpha$ とする。平面 $\alpha$ 上に点 P を，直線 AP が平面 $\alpha$ と直交するようにとる。線分 AP の長さ，および四面体 OAMN の体積を求めなさい。

三平方の定理

(1)から始めます。

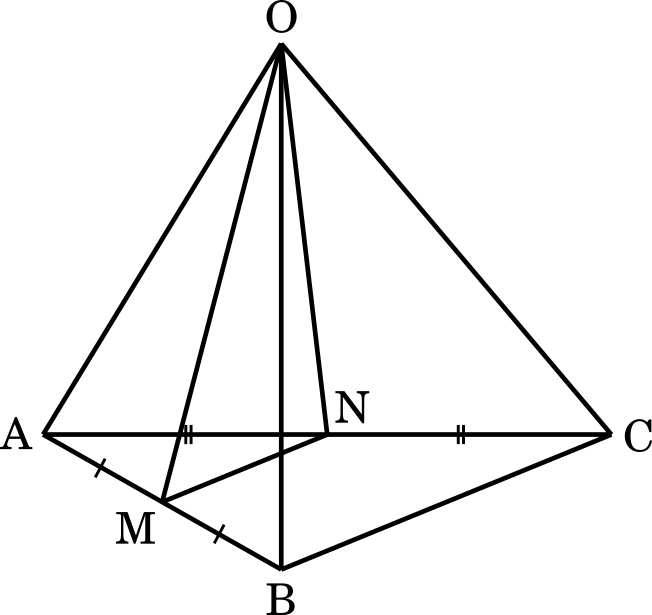
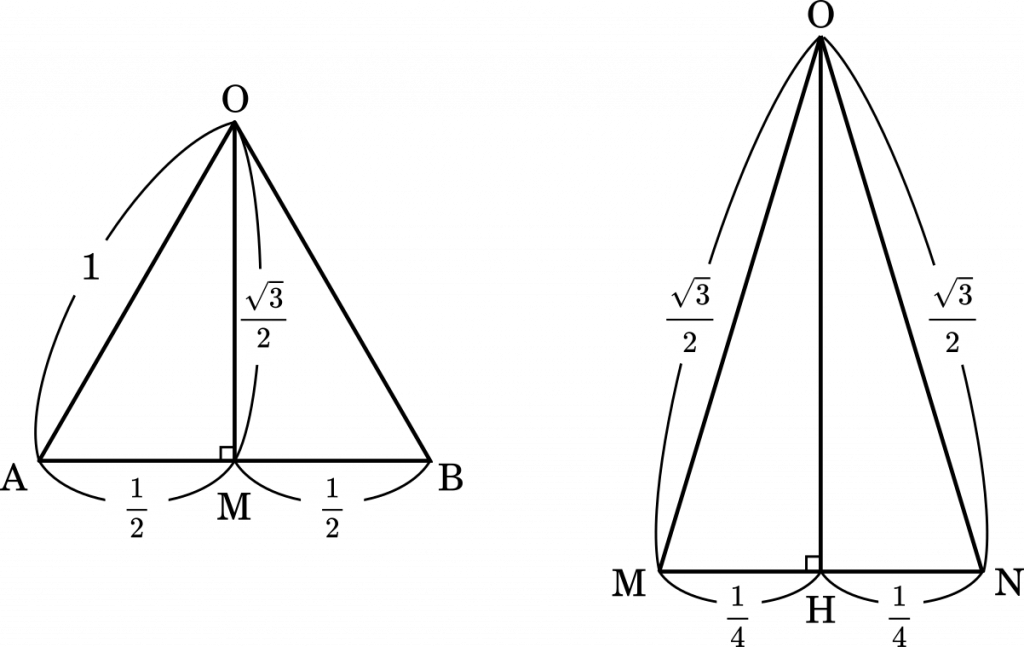
初めに，OM の長さから求めます。△OAB は正三角形なので，△OAMは辺の比が $1:2:\sqrt{3}$ になります。よって，OM ＝ ON ＝ $\cfrac{\sqrt{3}}{2}$ です。

今度は △OMN を考えてみましょう。

中点連結定理より BC の長さが 1 なら，MN の長さは $\cfrac{1}{2}$ です。そして，点 O から MN に垂線を下ろし，その足を H とすると MN の長さは $\cfrac{1}{4}$ となります。

ここから，OH の長さを求めましょう。三平方の定理より
$\Big(\cfrac{1}{4}\Big)^2+\text{OH}^2=\Big(\cfrac{\sqrt{3}}{2}\Big)^2$
$\text{OH}^2=\Big(\cfrac{\sqrt{3}}{2}\Big)^2-\Big(\cfrac{1}{4}\Big)^2$
$=\cfrac{3}{4}-\cfrac{1}{16}=\cfrac{12-1}{16}$
$=\cfrac{11}{16}$
$\text{OH}=\cfrac{\sqrt{11}}{4}$

これが三角形の高さになります。したがって，△OMN の面積は

$S=\cfrac{1}{2}\cdot\cfrac{1}{2}\cdot\cfrac{\sqrt{11}}{4}=\cfrac{\sqrt{11}}{16}$　（答え）

3 辺の長さをもとに三角形の高さを求める

(2)に進みます。

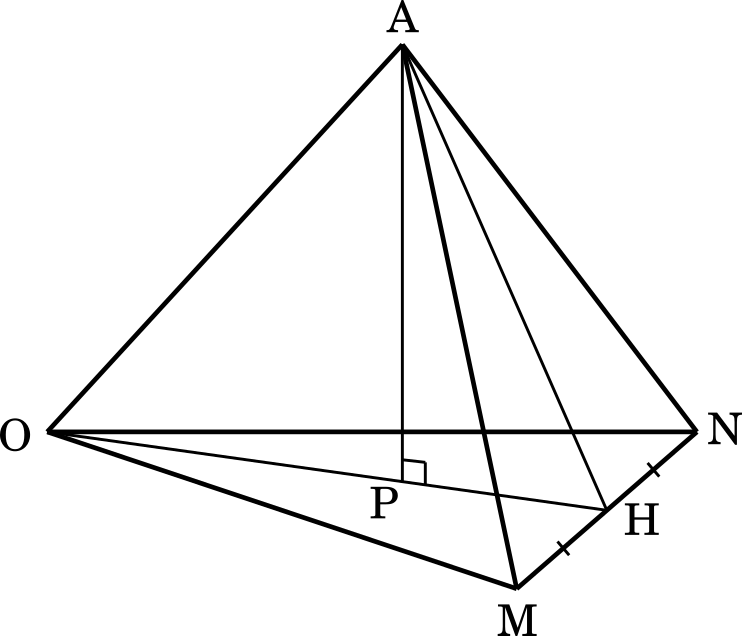
点 A から △OMN に垂線を下ろすと，点 P は OH 上にあります。求めたいのは AP の長さなので，△OAH について考えていくことになります。その前に，AH の長さを求めておきましょう。

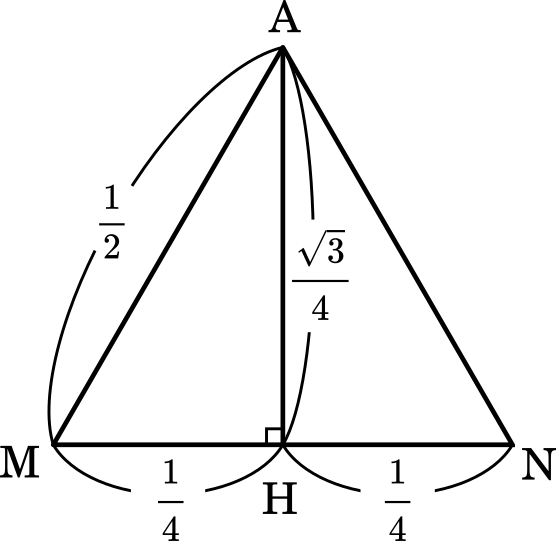
△AMN は辺の長さが $\cfrac{1}{2}$ の正三角形です。△AMH は辺の長さの比が $1:2:\sqrt{3}$ の直角三角形だから，AH の長さは $\cfrac{\sqrt{3}}{4}$ です。

△OAH を図に描いてみましょう。実は，点 P は OH の延長線上にできるのですが，OH の間にあるように図を描いても最終的な答えは一致します。ここで求めたいのは AP の長さです。

三平方の定理より

$\Big(\cfrac{\sqrt{11}}{4}+x\Big)^2+h^2=1$ ・・・①
$x^2+h^2=\Big(\cfrac{\sqrt{3}}{4}\Big)^2$　・・・②

①－②

$\Big(\cfrac{\sqrt{11}}{4}+x\Big)^2-x^2=1-\Big(\cfrac{\sqrt{3}}{4}\Big)^2$

式を整理して

$\cfrac{11}{16}+\cfrac{\sqrt{11}}{2}x+x^2-x^2=1-\cfrac{3}{16}$
$\cfrac{\sqrt{11}}{2}x=\cfrac{1}{8}$
$x=\cfrac{1}{4\sqrt{11}}$

②に代入して

$\Big(\cfrac{1}{4\sqrt{11}}\Big)^2+h^2=\Big(\cfrac{\sqrt{3}}{4}\Big)^2$
$h^2=\Big(\cfrac{\sqrt{3}}{4}\Big)^2-\Big(\cfrac{1}{4\sqrt{11}}\Big)^2$
$=\cfrac{3}{16}-\cfrac{1}{16\cdot11}$
$=\cfrac{3\cdot11-1}{16\cdot11}$
$=\cfrac{32}{16\cdot11}$
$=\cfrac{2}{11}$

よって

$h=\sqrt{\cfrac{2}{11}}=\cfrac{\sqrt{22}}{11}$　（答え）

また，OAMN の体積は

$V=\cfrac{1}{3}\cdot\triangle\sf{OMN}\cdot\sf{AP}$
$=\cfrac{1}{3}\cdot\cfrac{\sqrt{11}}{16}\cdot\cfrac{\sqrt{22}}{11}$

このまま計算すると大変なので，$\cfrac{\sqrt{22}}{11}$ は有理化する前の $\sqrt{\cfrac{2}{11}}$ を利用しましょう。

$=\cfrac{1}{3}\cdot\cfrac{\sqrt{11}}{16}\cdot\cfrac{\sqrt{2}}{\sqrt{11}}$
$=\cfrac{\sqrt{2}}{48}$　（答え）

四面体の問題が解けるかどうかは，ほとんど作図にかかっています。今回も図をたくさん描きましたが，勘違いを防ぐためにも一つずつなるべく丁寧に作図するようにしましょう。