方程式の解が複素数のとき，その共役な複素数も解であることの証明(東京都立大2018文系第3問)

$i$ を虚数単位とする。$m$ を整数とし，$g(x)=x^3-5x^2+mx-13$ とする。整数 $a$ と $0$ でない整数 $b$ が $g(a+bi)=0$ をみたすとき，以下の問いに答えなさい。（東京都立大2018）

(1) $g(a-bi)=0$ が成り立つことを示しなさい。

(2) $g(x)$ が $x^2-2ax+a^2+b^2$ で割り切れることを示しなさい。

(3) $m$ の値を求めなさい。

因数定理と剰余の定理

(1)から始めます。

$g(a+bi)=0$ をみたすということは，方程式の解の一つが $a+bi$ であるということです。$g(a-bi)=0$ も同様で，解の一つが $a-bi$ であるということです。

$x^3-5x^2+mx-13$ は 3 次関数ですが，そもそも解の一つが複素数 $a+bi$ であるとき，一般的にその共役な複素数 $a-bi$ も解であることは教科書に書いてある話です。

$a+bi$ と $a-bi$ が解であるなら，式は

$g(x)=(x-a-bi)(x-a+bi)Q(x)$ 

という形に因数分解できるはずです。

簡単な例で考えてみましょう。$x^3-6x^2+11x-6=0$ という方程式があったとして，これを因数分解すると

$(x-1)(x-2)(x-3)=0$

となります。このとき，$x=1,2,3$ が方程式の解です。これに $x=1$ を代入すると

$(1-1)(x-2)(x-3)$
$0\times(x-2)(x-3)=0$

となるので，イコール 0 が成り立ちます。$x=2$，$x=3$ のときも同様です。

このように，ある関数は $x-\sf{解}$ で因数分解できます。これは言い換えると，式は $x-\sf{解}$ で割り切れる（余りが 0 になる）ということです（因数定理）。

話を戻しましょう。$g(x)$ の解が $a+bi$ だけでなく $a-bi$ も解であると仮定するなら

$g(x)=(x-a-bi)(x-a+bi)Q(x)$ 

と因数分解できるはずです。

さらに余りを考えてみます。ある数は　割る数×商＋余り　という形で表すことができました。

$x^3-5x^2+mx-13$ は $x$ の 3 次式です。これを，$x-(a+bi)$，つまり 1 次式で割ると，その余りは 2 次以下の式になります。

そこで，余りを $px^2+qx+r$ と表してみます。

$\begin{cases}g(x)=(x-a-bi)(x-a+bi)Q(x)+R(x)\\R(x)=px^2+qx+r\end{cases}$

このとき，$x$ に $a+bi$ を代入しても，$a-bi$ を代入しても，式は割り切れるから余りは 0，つまり $R(x)=0$ が成り立ちます。

$R(a+bi)=p(a+bi)^2+q(a+bi)+r$
$=a^2p+2abpi-b^2p+aq+bqi+r=0$

ここで，式を実数と虚数に分けて整理します。

$a^2p-pb^2+aq+r+(2abp+bq)i=0$

式が 0 になるということは，実数の部分と虚数の部分がどちらも 0 になるということです。

よって

$\begin{cases}a^2p-b^2p+aq+r=0&\cdots\sf{①}\\2abp+bq=0&\cdots\sf{②}\end{cases}$

これを利用します。

$R(a-bi)=p(a-bi)^2+q(a-bi)+r$
$=a^2p-2abpi-b^2p+aq-bqi+r$
$=a^2p-b^2q+aq+r-(2abp+bq)i$

①，②を代入すると

$=0$　（証明終わり）

式を展開する

(2)に進みます。

(1)より

$g(x)=(x-a-bi)(x-a+bi)Q(x)$ 

として，カッコを展開します。

$=\{x-(a+bi)\}\{x-(a-bi)\}Q(x)$ 

$=\{x^2-(a-bi)x-(a+bi)x+(a+bi)(a-bi)\}Q(x)$
$=(x^2-ax+bix-ax-bix+a^2+b^2)Q(x)$
$=(x^2-2ax+a^2+b^2)Q(x)$

（証明終わり）

式を割る

(3)に進みます。このままでは手がかりがないので，式を実際に $x^2-2ax+a^2+b^2$ で割ってみると良いでしょう。

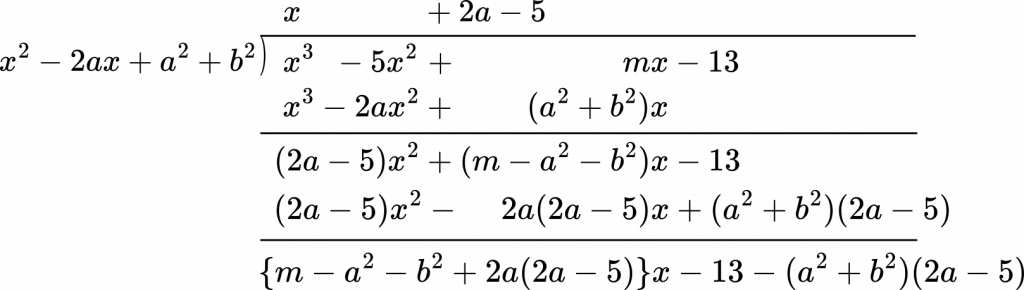
式は割り切れるので，余りは 0 です。
ここから，式が 0 になる条件を考えると

$\begin{cases}m-a^2-b^2+2a(2a-5)=0\\-13-(a^2+b^2)(2a-5)=0\end{cases}$

という式を作ることができます。式を変形すると

$\begin{cases}m=-3a^2+b^2+10a&\cdots\sf{③} \\　(a^2+b^2)(2a-5)=-13&\cdots\sf{④}\end{cases}$

④から片づけていきましょう。右辺が 13 であるということは，左辺は $1\times13$ または $13\times1$ のかけ算のパターンしかないことが分かります。また，$a^2+b^2$ は $a,b$ がどんな値でも正の数になります。よって，左辺は $1\times(-13)$ または $13\times(-1)$ です。

(i) $a^2+b^2=1$，$2a-5=-13$ のとき
$2a-5=-13$
$2a=-8$
$a=-4$

$a^2+b^2=1$ に代入すると

$16+b^2=1$
$b^2=-15$
$b=\pm\sqrt{15}$

$b$ は整数だから，不適。

(ii) $a^2+b^2=13$，$2a-5=-1$ のとき

$2a-5=-1$
$2a=4$
$a=2$

$a^2+b^2=1$ に代入すると

$4+b^2=13$
$b^2=9$
$b=\pm3$

よって，$a=2$，$b=\pm3$

これらを③に代入すると

$m=-3\cdot2^2+3^2+10\cdot2$
$=17$　（答え）