【数III積分】円すいの体積の公式を回転体の体積として求めてみる/公式に1/3がある理由
中学で円すいの体積は
$V=\cfrac{1}{3}\times$ 底面積 $\times$ 高さ
であると習いました。
とは言え,$\cfrac{1}{3}$ って何?と思ったことはないでしょうか。

この公式は,円すいだけでなく角すいでも使えます。実のところ底面の形が何であろうと関係なく,それがすい体であるならば同じ公式が使えます。
この謎は中学校では説明されませんが,高校生なら積分を使って解き明かすことができます。
円すいの体積
まずは,円すいの体積を積分で求めてみましょう。
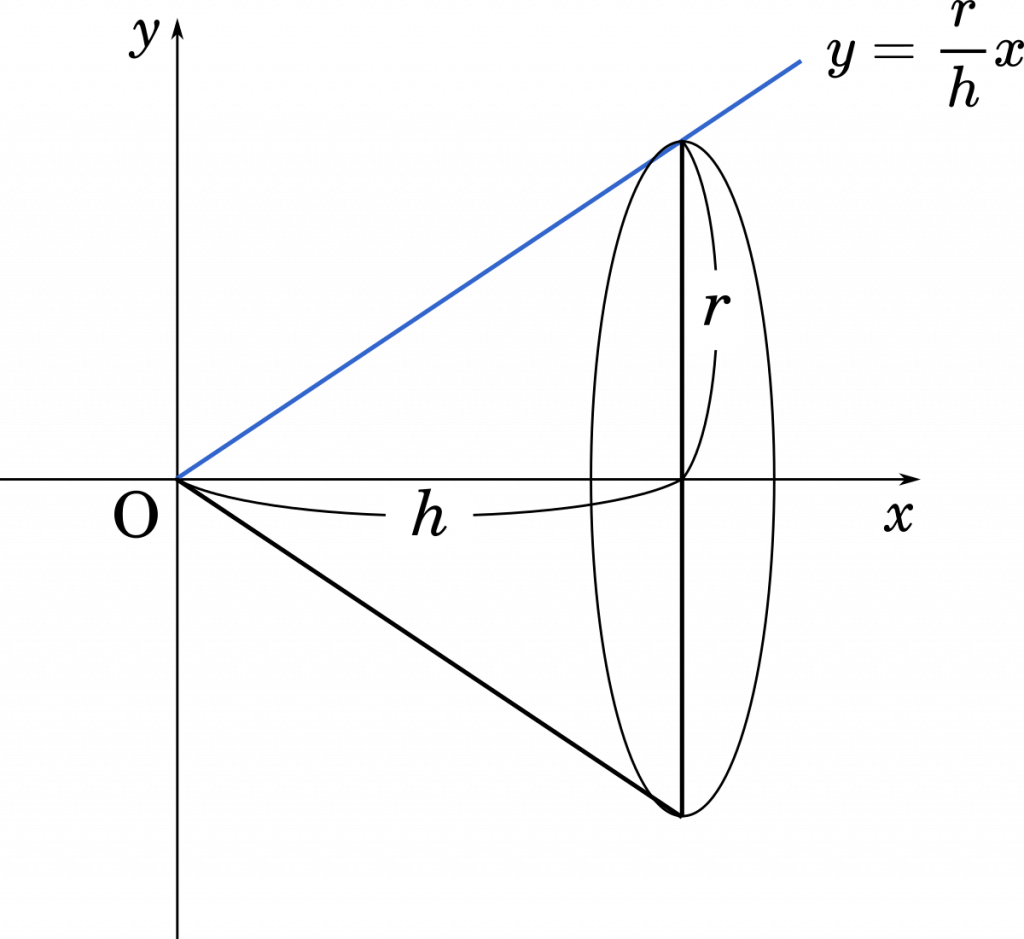
円すいを横に倒してグラフにすると,回転体として考えることができます。
底面の半径を $r$,高さを $h$ とすると,直線は $y=\cfrac{r}{h}x$ として表すことができます。

回転体の体積は,円の面積を積み重ねることによって求めることができます。つまり
$\displaystyle V=\int_0^h S\enspace dx$
となります。
円の面積は $S=\pi r^2$,$r=\cfrac{r}{h}x$ だから
$S=\pi\Big(\cfrac{r}{h}x\Big)^2$
$=\cfrac{r^2\pi}{h^2}x^2$
よって
$\displaystyle V=\int_0^h \cfrac{r^2\pi }{h^2}x^2\enspace dx$
$=\cfrac{r^2\pi }{h^2}\Big[\cfrac{x^3}{3}\Big]_0^h$
$=\cfrac{r^2\pi}{h^2}\cdot\cfrac{h^3}{3}$
$=\cfrac{hr^2\pi}{3}$
つまり
$V=\cfrac{1}{3}\times \pi r^2\times h$
これで,円すいの体積が $V=\cfrac{1}{3}\times$ 底面積 $\times$ 高さ であることが分かりました。


すい体の体積
次に,底面が円でないときを考えてみましょう。
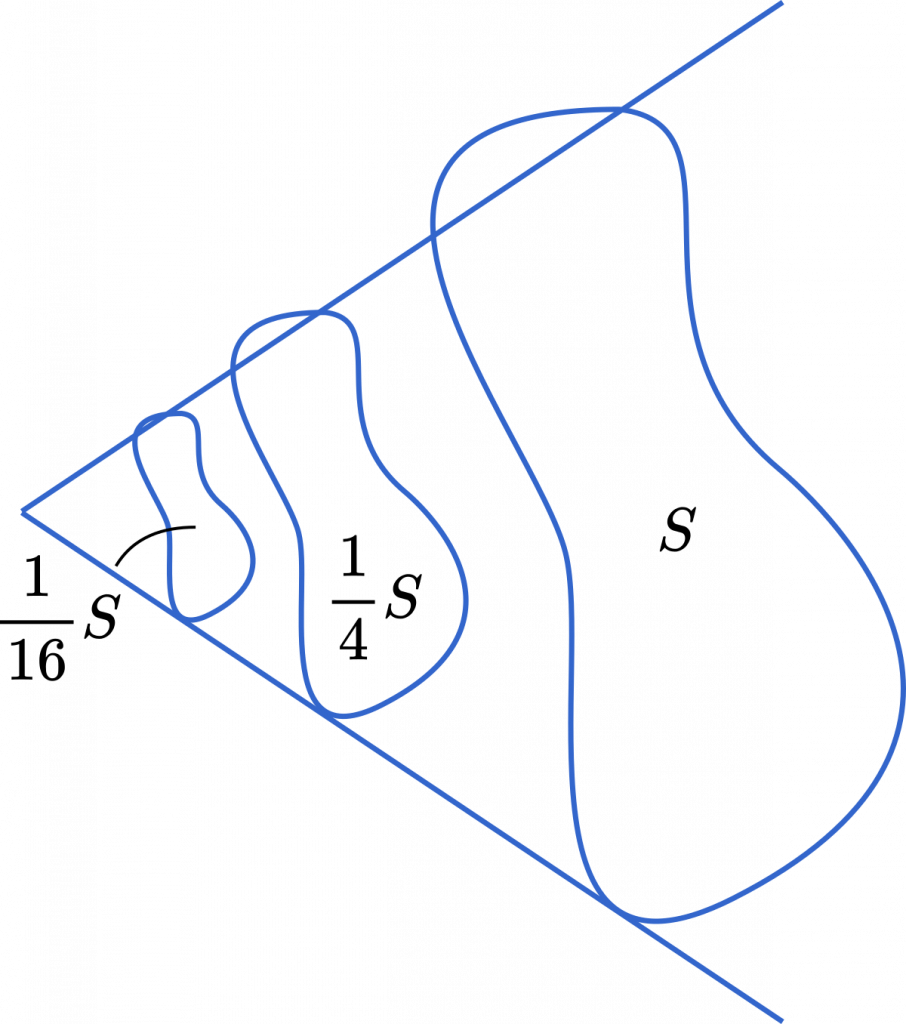
ある2つの相似な図形があるとき,その面積の比は辺の比の2乗となります。たとえば,辺の比が $1:2$ なら,面積の比は $1:2^2=1:4$ となるのでした。
いったん,すい体の高さを 1 として,高さと面積の関係をグラフで表してみると,2 次関数のグラフができあがります。
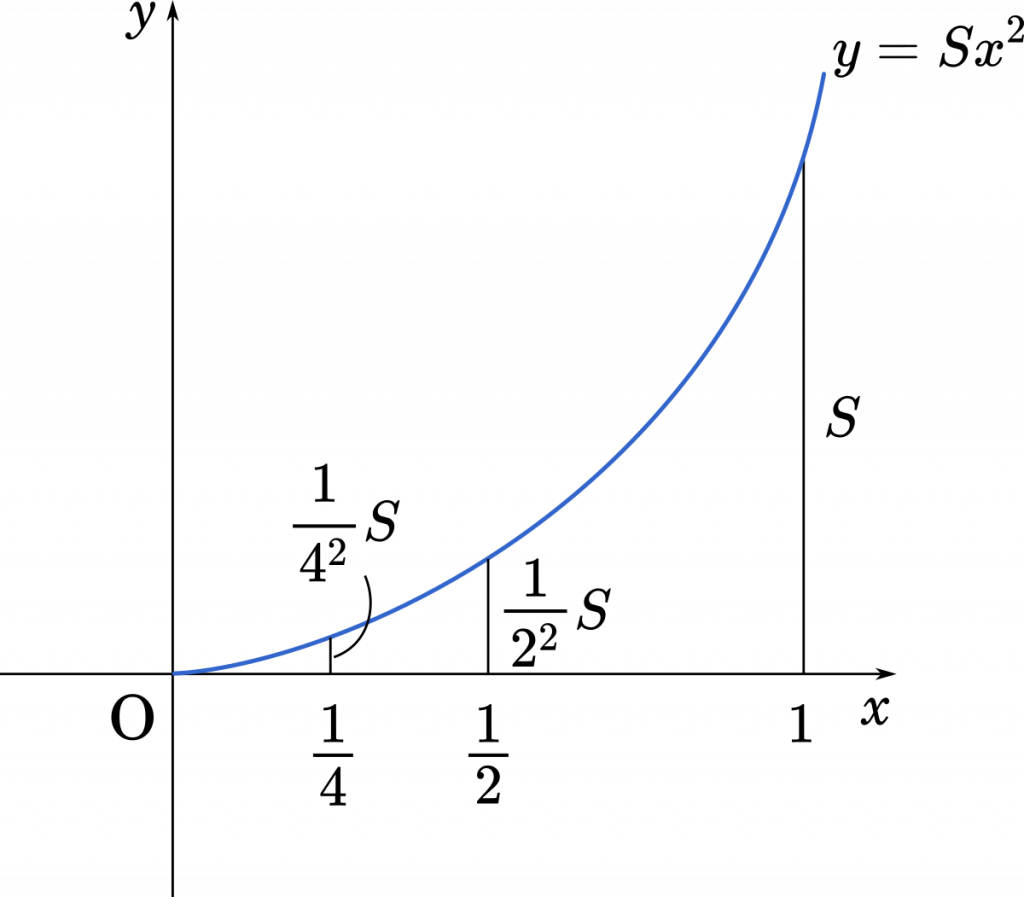
高さが 1 のときの面積を $S$ とすると,高さが $\cfrac{1}{2}$ のときの面積は $\Big(\cfrac{1}{2}\Big)^2S=\cfrac{1}{4}S$,高さが $\cfrac{1}{4}$ のときの面積は $\Big(\cfrac{1}{4}\Big)^2S=\cfrac{1}{16}S$ となります。
よって,この関数は $y=Sx^2$ として表すことができます。
これを積分して体積を求めてみましょう。
$\displaystyle V=\int_0^1 Sx^2\enspace dx$
$=S\Big[\cfrac{1}{3}x^3\Big]_0^1$
$=\cfrac{1}{3}S$
高さを h とする
次に,すい体の高さが $h$ である場合を考えてみましょう。
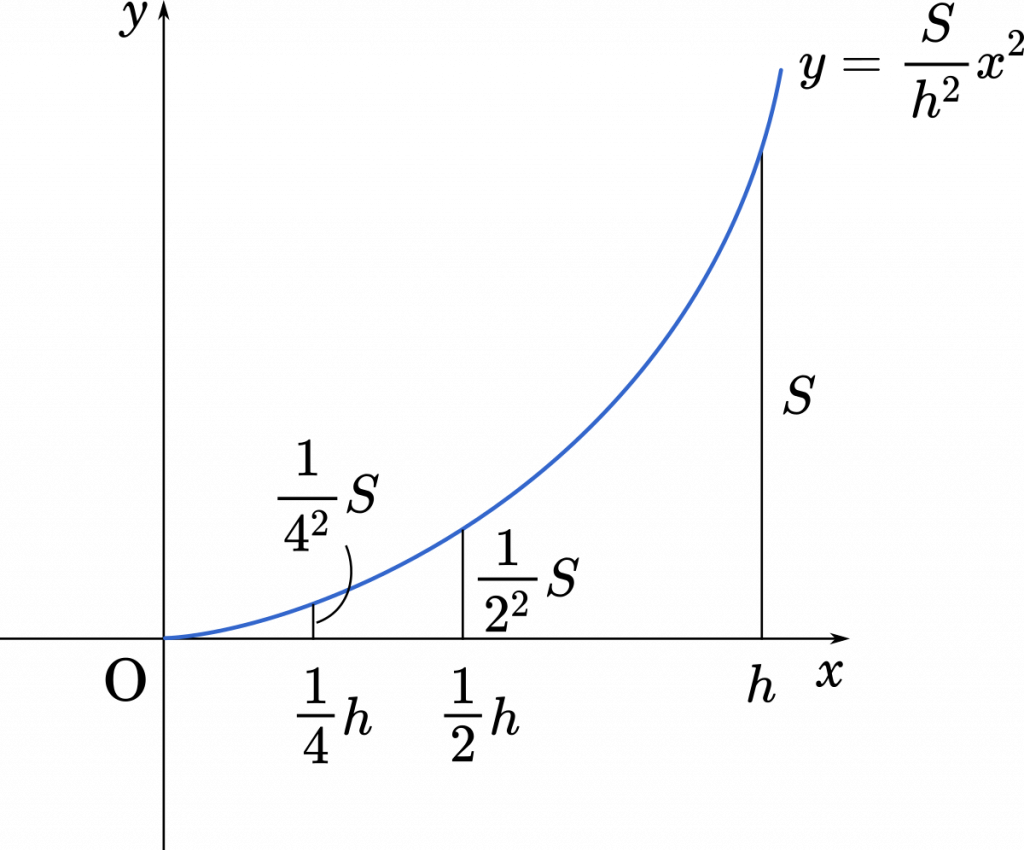
高さが $h$ のときの面積を $S$ とするなら,高さが $\cfrac{1}{2}h$ のときの面積はやはり $\Big(\cfrac{1}{2}\Big)^2S$ となります。面積の比は辺の長さの比の2乗だからです。
この関数は $y=\cfrac{S}{h^2}x^2$ となります。
$x=h$ を代入すると $y=S$ となり,ちゃんとつじつまが合っているのが分かります。
これを積分すると
$\displaystyle V=\int_0^h \cfrac{S}{h^2}x^2\enspace dx$
$=\cfrac{S}{h^2}\Big[\cfrac{1}{3}x^3\Big]_0^h$
$=\cfrac{S}{h^2}\cdot\cfrac{1}{3}h^3$
$=\cfrac{1}{3}Sh$
これで,体積=$\cfrac{1}{3}\times$ 底面積 × 高さ の公式ができあがりました。
まとめ
ここでは,円すいの体積を回転体として捉え,積分によって求めました。また,相似な図形の面積比の関係を利用して,底面がどのような形であっても,同じ式が成り立つことを学びました。
すい体の公式に $\cfrac{1}{3}$ が含まれるのは,面積の比が辺の比の2乗であるため,それを積分したときに $\cfrac{1}{3}$ という係数が出現するからである,と結論付けることができます。
SNSでシェア