【高校化学基礎まとめ】金属結晶の充填率の求め方
結晶格子 金属原子が規則正しく立体的に配列した構造を結晶格子という。
単位格子 結晶格子の最小の繰り返し単位を単位格子という。
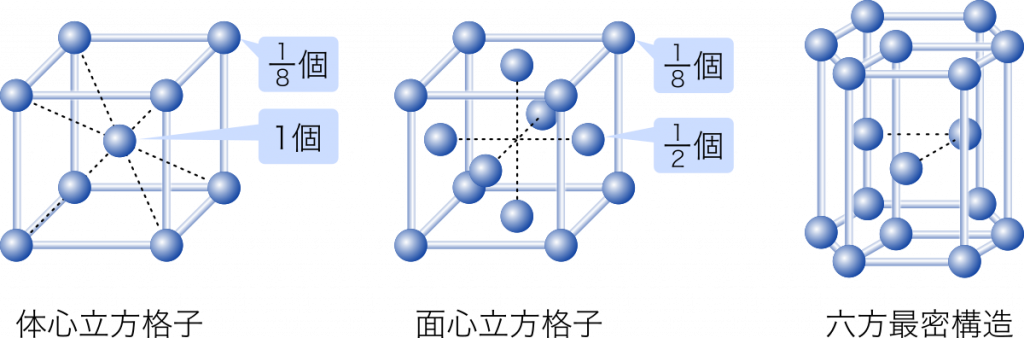
配位数 原子 1 個に着目して,その原子から最も近いところにあるほかの原子の数を配位数という。体心立方格子の配位数は 8,面心立方格子は 12,六方最密構造は 12。
単位格子中に含まれる原子の数
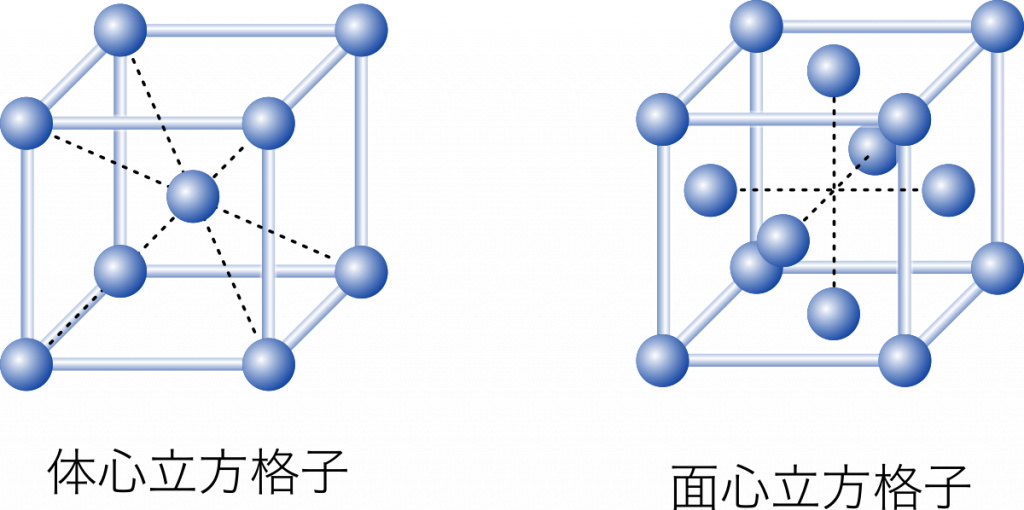
単位格子中に含まれる原子の数を数えてみましょう。
体心立方格子は,さいころの形をいくつも並べた構造をしています。このとき,さいころの角にある原子はとなりのさいころと共有されているので,そのまま 1 個として数えると原子の数を数えすぎることになります。角にある原子はとなり合う 8 個のさいころで共有されるので,$\cfrac{1}{8}$ 個として数えます。
単位格子中に含まれる原子の数は,体心立方格子の場合
$1+\cfrac{1}{8}\times8=2$ 個
面心立方格子の場合
$\cfrac{1}{2}\times6+\cfrac{1}{8}\times8=4$ 個
となります。
ちなみに,六方最密構造の単位格子中に含まれる原子の数は 2 個です。
充填率の求めかた
充填率 単位格子中における原子の占める体積の割合を充填率という。
体心立方格子の場合
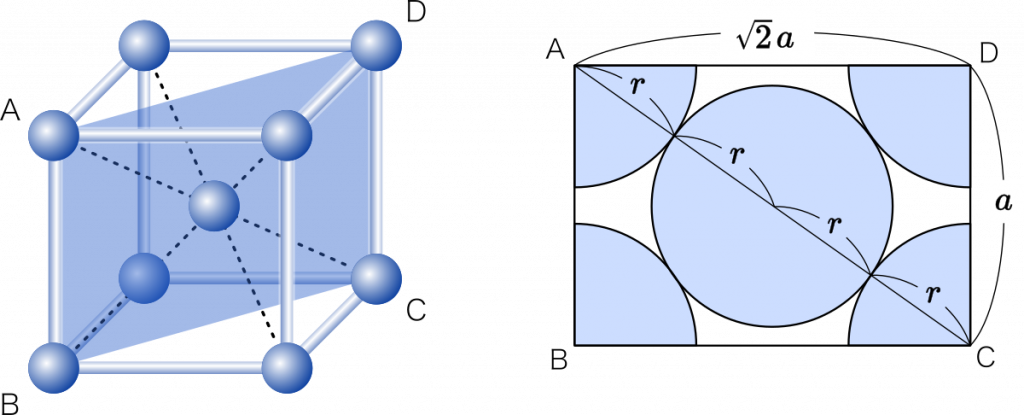
充填率とは,簡単に言えばさいころの体積に対する原子の体積の割合ということだから,原子の体積が分かればすぐに求めることができます。原子は球だから,球の半径が分かれば体積を求めることができます。とは言え,球の半径の求め方は少し注意が必要です。
体心立方格子の場合は,さいころを斜め方向に切断します。さいころの 1 辺の長さを $a$ とすると,三平方の定理より,斜め部分の長さは $\sqrt{2}a$ となります。切断面を図に描いてみると,球の半径 $r$ は直線 AC を 4 分割した長さであることが分かります。$r$ を求めてみましょう。
ポイント はじめに,格子の 1 辺の長さを $a$ とする。
△ACDは直角三角形だから,三平方の定理より
$a^2+(\sqrt{2}a)^2=(4r)^2$
$a^2+2a^2=16r^2$
$3a^2=16r^2$
$r^2=\cfrac{3}{16}a^2$
$r>0$ より
$r=\cfrac{\sqrt{3}}{4}a$
球の体積の公式 $V=\cfrac{4\pi r^3}{3}$ を用いて
原子 1 個の体積は
$\cfrac{4\pi r^3}{3}=\cfrac{4\pi}{3}\times\Big(\cfrac{\sqrt{3}}{4}a\Big)^3$
$=\cfrac{4\pi}{3}\times\cfrac{3\sqrt{3}}{64}a^3$
$=\cfrac{\sqrt{3}a^3\pi}{16}$
ここで,単位格子中に含まれる原子の数は 2 個であることを思い出しましょう。よって,球の体積に 2 をかけます。
さいころの体積は $a^3$ だから,充填率は
$\cfrac{\enspace2\times\cfrac{\sqrt{3}a^3\pi}{16}\enspace}{a^3}=\cfrac{\sqrt{3}}{8}\pi\fallingdotseq0.68$ (答え)
次に,面心立方格子の場合です。
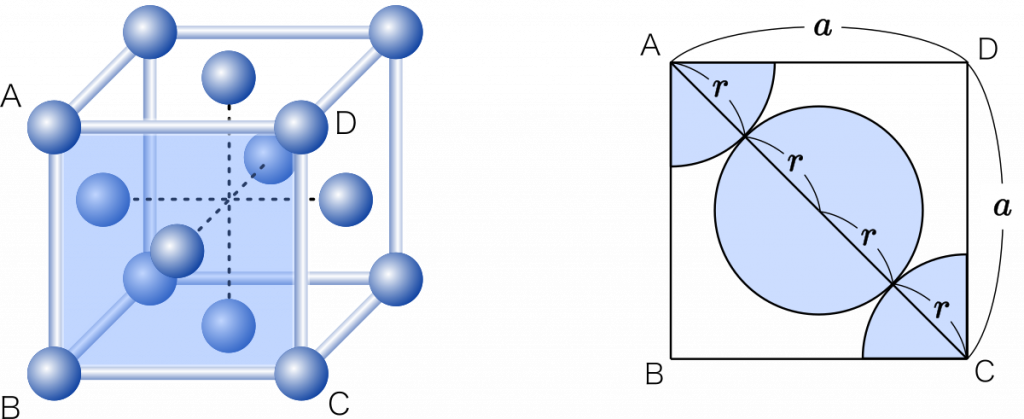
面心立方格子の場合は,さいころの面で考えます。$r$ を求めてみましょう。
三平方の定理より
$a^2+a^2=(4r)^2$
$2a^2=16r^2$
$r^2=\cfrac{1}{8}a^2$
$r>0$ より
$r=\cfrac{\sqrt{2}}{4}a$
原子 1 個の体積は
$\cfrac{4\pi}{3}\times\Big(\cfrac{\sqrt{2}}{4}a\Big)^3$
$=\cfrac{4\pi}{3}\times\cfrac{\sqrt{2}}{32}a^3$
$=\cfrac{\sqrt{2}a^3\pi}{24}$
単位格子中に含まれる原子の数は 4 個でした。したがって,充填率は
$\cfrac{\enspace4\times\cfrac{\sqrt{2}a^3\pi}{24}}{a^3}=\cfrac{\sqrt{2}} {6}\pi\fallingdotseq0.74$ (答え)
六方最密構造の場合,充填率は面心立方格子と同じ,0.74 です。
SNSでシェア