nx をもつ関数の不等式の証明・極限を求める/中間値の定理(神戸大2017理系第1問)
$n$ を自然数とする。
$f(x)=\sin x-nx^2+\cfrac{1}{9}x^3$
とおく。$3<\pi<4$ であることを用いて,以下の問に答えよ。
(1) $0<x<\cfrac{\pi}{2}$ のとき,$f”(x)<0$ であることを示せ。
(2) 方程式 $f(x)=0$ は $0<x<\cfrac{\pi}{2}$ の範囲に解をただ 1 つもつことを示せ。
(3) (2)における解を $x_n$ とする。$\displaystyle\lim_{n\rightarrow\infty}x_n=0$ であること示し,$\displaystyle\lim_{n\rightarrow\infty}nx_n$ を求めよ。
不等式の証明
(1)から始めます。
まずは第二次導関数から求めましょう。
$f'(x)=\cos x-2nx+\cfrac{1}{3}x^2$
$f”(x)=-\sin x-2n+\cfrac{2}{3}x$
$0<x<\cfrac{\pi}{2}$ より
$-1<-\sin x<0$ ・・・①
また
$0<\cfrac{2}{3}\pi<\cfrac{2}{3}\cdot\cfrac{\pi}{2}$
$0<\cfrac{2}{3}x<\cfrac{\pi}{3}$ ・・・②
①+②
$-1<-\sin x+\cfrac{2}{3}x<\cfrac{\pi}{3}$
さらに,$f”(x)$ に合わせていきます。
$-1-2n<-\sin x-2n+\cfrac{2}{3}x<\cfrac{\pi}{3}-2n$
よって
$f”(x)<\cfrac{\pi}{3}-2n$
あとは $\cfrac{\pi}{3}-2n$ が負の数であることを示せば,$f”(x)<0$ が成り立つことになります。
$3<\pi<4$ より
$1<\cfrac{\pi}{3}<\cfrac{4}{3}$
$1-2n<\cfrac{\pi}{3}-2n<\cfrac{4}{3}-2n$
よって
$f”(x)<\cfrac{\pi}{3}-2n<\cfrac{4}{3}-2n$
$f”(x)<\cfrac{4}{3}-2n$
$n$ は自然数だから,$n\geqq1$ です。したがって,$2n\geqq2$ となるので,$\cfrac{4}{3}-2n$ はつねに負の数となります。
$f”(x)<\cfrac{4}{3}-2n<0$
$f”(x)<0$ (証明終わり)
中間値の定理
(2)に進みます。
ここでは中間値の定理を用いてみます。


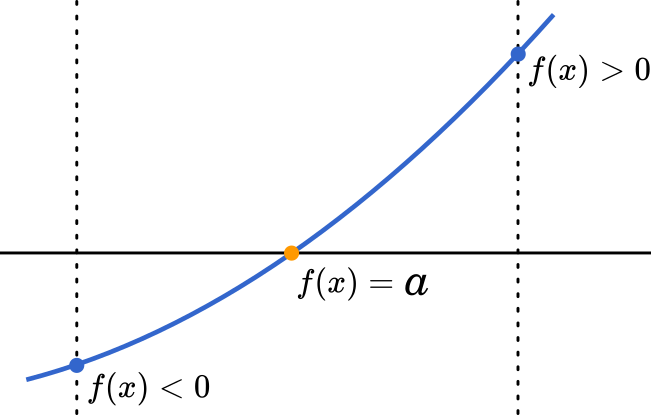


そこで,いったん増減表を作ってグラフの増減を確認してみましょう。
$f'(0)=1$
$f’\Big(\cfrac{\pi}{2}\Big)=-2n\cdot\cfrac{\pi}{2}+\cfrac{1}{3}\Big(\cfrac{\pi}{2}\Big)^2$
$=-n\pi+\cfrac{\pi^2}{12}$
$=\cfrac{\pi(\pi-12n)}{12}$
$3<\pi<4$ と $n\geqq1$ より $\pi-12n$ はつねに負の値です。
$\cfrac{\pi(\pi-12n)}{12}<0$
また
$f(0)=0$
$f\Big(\cfrac{\pi}{2}\Big)=1-\cfrac{n}{4}\pi^2+\cfrac{\pi^3}{72}$
$=\cfrac{72-18n\pi^2+\pi^3}{72}$

$3<\pi<4$ より
$9<\pi^2<16$
$162n<18n\pi^2<288n$
$-288n<-18n\pi^2<-162n$
また
$3<\pi<4$
$27<\pi^3<64$
不等式の右側について
$72-18n\pi^2+\pi^3<72-162n+64$
$72-18n\pi^2+\pi^3<136-162n<0$
よって,負の値です。
増減表は
$\def\arraystretch{1.5}\begin{array}{|c|c|c|c|c|c|c|c|}\hline x&(0)&\cdots&\alpha&\cdots&\beta&\cdots&\left(\frac{\pi}{2}\right)\\\hline f'(x)&(+)&+&0&-&-&-&(-)\\\hline f”(x)&&-&-&-&-&-\\\hline f(x)&(0)&\nearrow&&\searrow&0&\searrow\\\hline\end{array}$
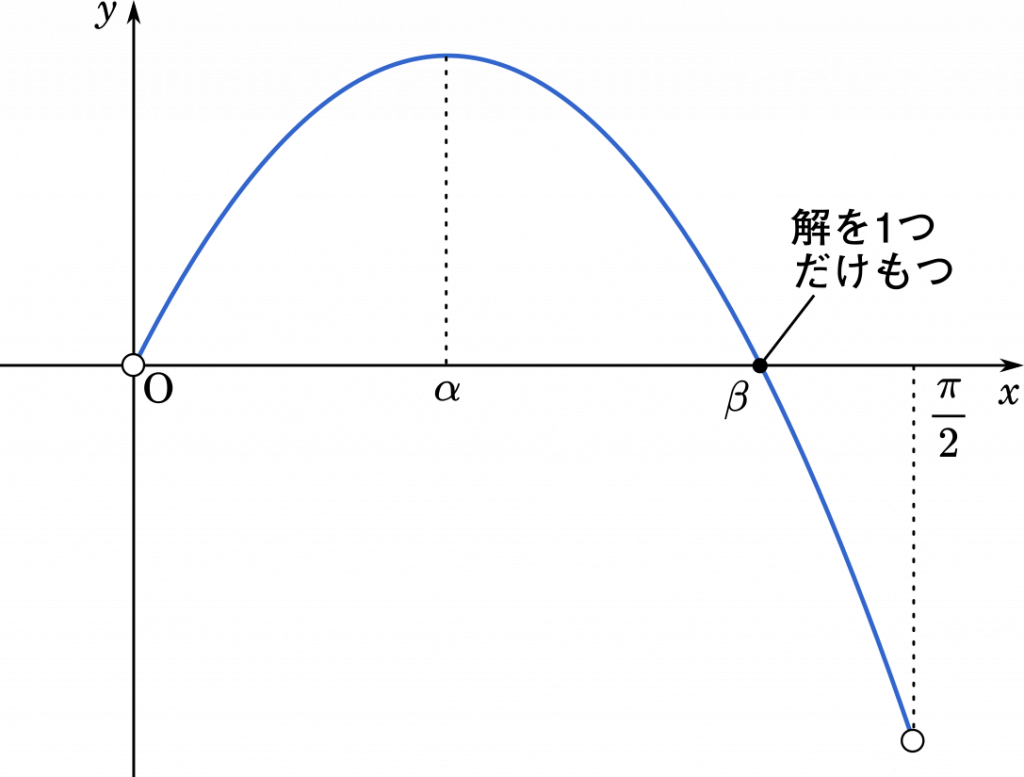
区間内で $f”(x)$ はつねに負の値なので,極値は存在しないか,または 1 個だけ存在することになります。ここでは,$f'(x)$ の正負が途中で入れ替わっているはずなので,$x=\alpha$ で極値をとるとしています。
その結果,$f(x)$ は $f(0)=0$ からスタートしていったん増加し,$x=\alpha$ から減少に転じ,そのあとはつねに減少します。そして $f\Big(\cfrac{\pi}{2}\Big)$ は負の値だったので,途中で $f(x)=0$ を通るはずです。

したがって,方程式 $f(x)=0$ は $0<x<\cfrac{\pi}{2}$ の範囲に解をただ 1 つもつ。(証明終わり)
極限を求める
(3)に進みます。
(2)における解を $x_n$ とするということは
$f(x_n)=0$
が成り立つということです。
$f(x_n)=\sin x_n-n{x_n}^2+\cfrac{1}{9}{x_n}^3=0$
$n{x_n}^2=\sin x_n+\cfrac{1}{9}{x_n}^3$ ・・・③
${x_n}^2=\cfrac{\sin x_n}{n}+\cfrac{{x_n}^3}{9n}$

$x_n$ はある決まった数(定数)だから,$\sin x_n$ と ${x_n}^3$ もなんらかの決まった数になるはずです。
よって
$\displaystyle\lim_{n\rightarrow\infty}{x_n}^2=0$
だから
$\displaystyle\lim_{n\rightarrow\infty}x_n=0$


$\displaystyle\lim_{n\rightarrow\infty}a_n=\alpha$,$\displaystyle\lim_{n\rightarrow\infty}b_n=\beta$ のとき
$\displaystyle\lim_{n\rightarrow\infty}a_nb_n=\alpha\beta$

あとは,$\displaystyle\lim_{n\rightarrow\infty}nx_n$ を求めましょう。
$n{x_n}^2=\sin x_n+\cfrac{1}{9}{x_n}^3$ ・・・③ より
$n{x_n}=\cfrac{\sin x_n}{x_n}+\cfrac{1}{9}{x_n}^2$
$\cfrac{\sin x}{x}$ の極限には公式がありました。
公式 $\displaystyle\lim_{x\rightarrow0}\cfrac{\sin x}{x}=1$
$n\rightarrow\infty$ のとき $x_n$ は 0 に収束するので
$\displaystyle\lim_{n\rightarrow\infty}\cfrac{\sin x_n}{x_n}=1$
となります。
よって
$\displaystyle\lim_{n\rightarrow\infty}\cfrac{\sin x_n}{x_n}+\cfrac{1}{9}{x_n}^2=1$ (答え)
SNSでシェア