二次関数と領域・x を定数と見なして考えてみる(横浜国立大2015理系第3問)

公開日:2021/07/23

最終更新日:2021/07/23

実数 $a$ に対し，$xy$ 平面上の放物線 $C:y=(x-a)^2-2a^2+1$ を考える。次の問いに答えよ。

(1) $a$ がすべての実数を動くとき，$C$ が通過する領域を求め，図示せよ。

(2) $a$ が $-1\leqq a\leqq1$ の範囲を動くとき，$C$ が通過する領域を求め，図示せよ。

x を固定して a を変化させる

(1)から始めます。

つかみどころがないカンジ。

式の形から，二次関数を $x$ 方向に $a$，$y$ 方向に $-a^2+1$ 平行移動させたグラフと言えます。しかし，グラフは $a$ の値によってさまざまな場所を通っていくので，そこから領域を考えるのは困難です。

解き方は 1 つではないのですが，今回はなるべくグラフをイメージできる形で解いていこうと思います。

上の図のように $x$ をいったん固定して，$a$ を変化させてみます。$x$ 座標を固定すると，$a$ の値によって $y$ の値が変化することになり，ある $x$ 座標における $y$ の値の範囲が見えてきます。

$C:y=(x-a)^2-2a^2+1$
$=-a^2-2xa+x^2+1$

式を $a$ の関数としてみなします。このとき，$x$ は定数扱いです。これを $a$ で微分して，増減表を作ってみましょう。

$f(a)=-a^2-2xa+x^2+1$ として
$f'(a)=-2a-2x$

$-2a-2x=0$ として
$a=-x$

$\def\arraystretch{1.5}\begin{array}{|c|c|c|c|c|c|}\hline a&(-\infty)&\cdots&-x&\cdots&(\infty)\\\hline f'(a)&&+&0&-&\\\hline f(a)&(-\infty)&\nearrow&&\searrow&(-\infty)\\\hline\end{array}$

$f(-x)=-(-x)^2-2x(-x)+x^2+1$
$=-x^2+2x^2+x^2+1$
$=2x^2+1$

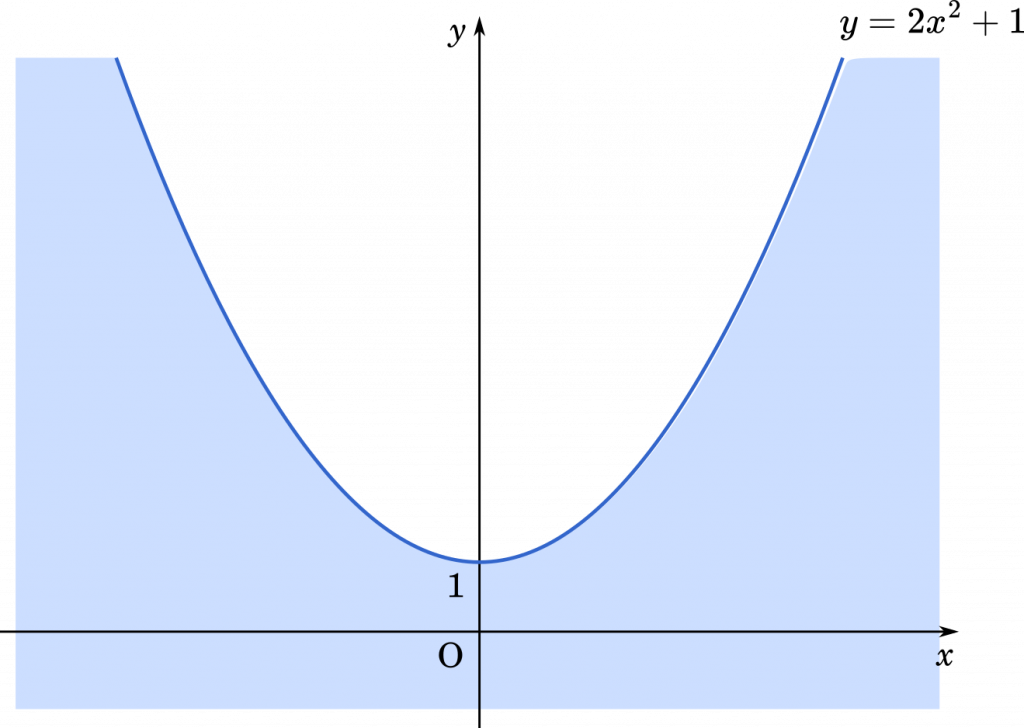
$a$ が実数全体で変化していくとき，$y=2x^2+1$ が $y$ の値の最大値です。

したがって

$y\leqq2x^2+1$　（答え）

場合分けして考える

(2)に進みます。

ここは，場合分けによって最大値と最小値を考えていきます。

(i) $-x\leqq-1$ のとき

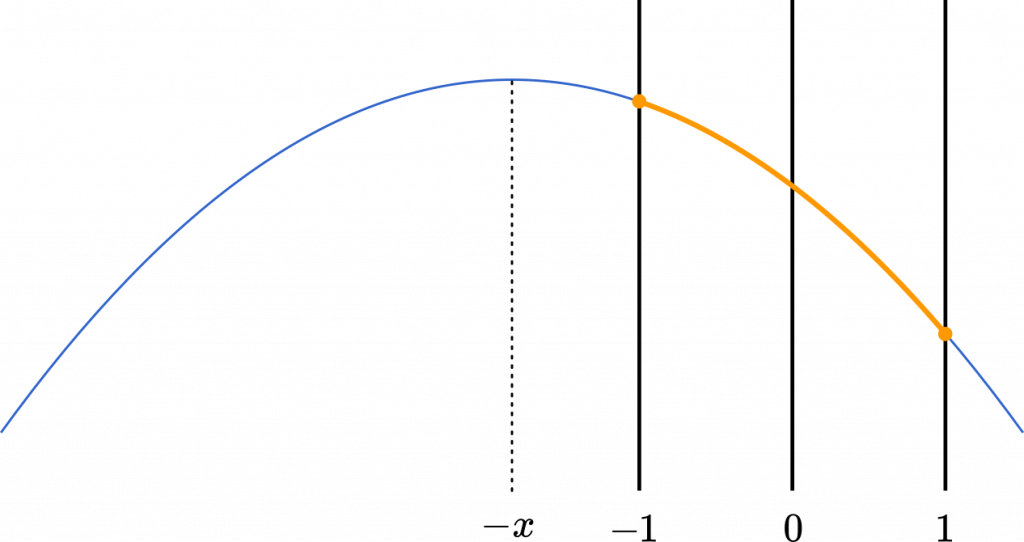
$-x\leqq-1$ は変形すると $x\geqq1$ です。

$f(a)$ は $a$ の二次関数なので，グラフを描いてみると，最大・最小を見つけることができます。

最大は $a=-1$ のとき

$f(-1)=-(-1)^2-2x(-1)+x^2+1$
$=-1+2x+x^2+1$
$=x^2+2x$

最小は $a=1$ のとき

$f(1)=-1-2x+x^2+1$
$=x^2-2x$

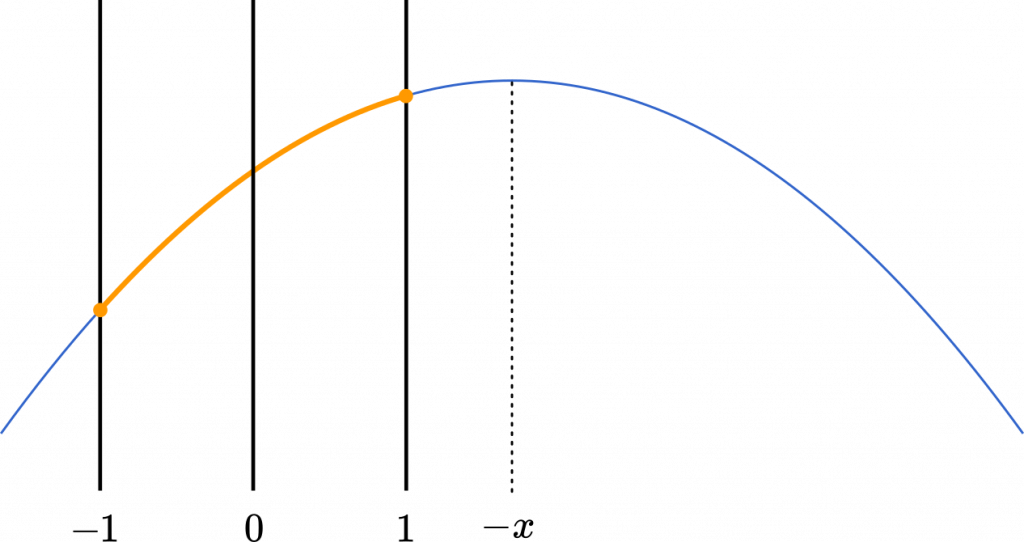
(ii) $-1<-x\leqq0$ のとき

$0\leqq x<1$

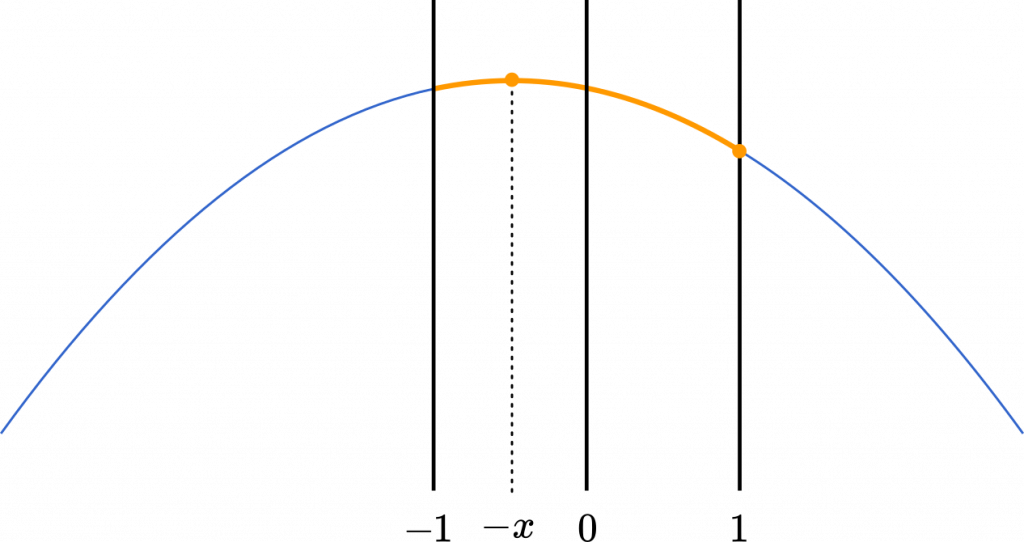
最大は $a=-x$ のとき

$f(-x)=2x^2+1$

最小は $a=1$ のとき

$f(1)=x^2-2x$

(iii) $0<-x\leqq1$ のとき

$-1\leqq x<0$

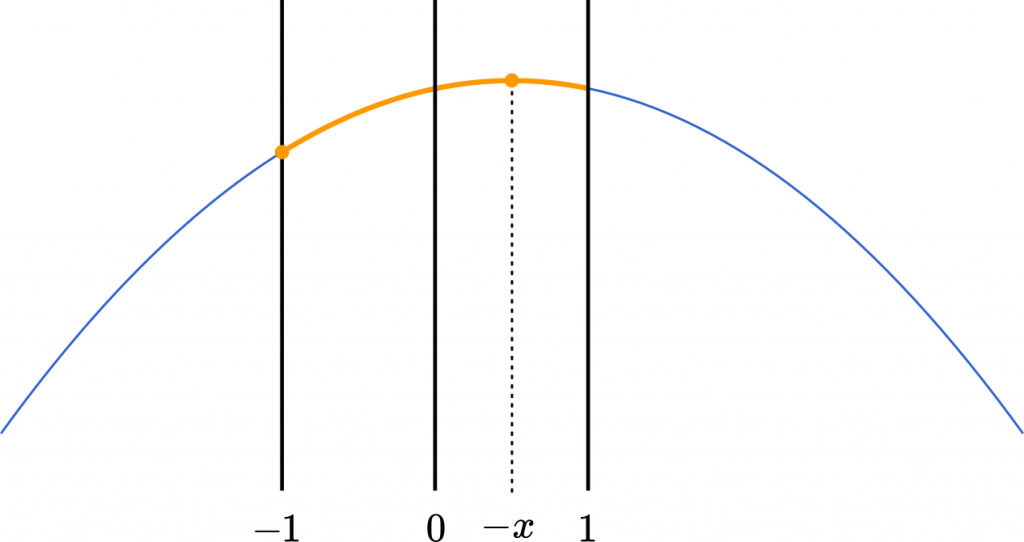
最大は $a=-x$ のとき

$f(-x)=2x^2+1$

最小は $a=-1$ のとき

$f(-1)=x^2+2x$

(iv) $1<-x$ のとき

$x<-1$

最大は $a=1$ のとき