【数IIB・III微分】二次関数と２つの接線の交点を求める(北海道大2021理系第2問)

$a$ を $a\not=-3$ を満たす定数とする。放物線 $y=\cfrac{1}{2}x^2$ 上の点 $\text{A}\Big(-1,\cfrac{1}{2}\Big)$ における接線を $\ell_1$，点 $\text{B}\Big(a+2,\cfrac{(a+2)^2}{2}\Big)$ における接線を $\ell_2$ とする。$\ell_1$ と $\ell_2$ の交点を C とおく。（北海道大2021）

(1) C の座標を $a$ を用いて表せ。

(2) $a$ が $a>0$ を満たしながら動くとき，$\cfrac{|\text{AB}|}{|\text{BC}|}$ が最小となるときの $a$ の値を求めよ。ただし，$|\text{AB}|$ および $|\text{BC}|$ はそれぞれ線分 AB と線分 BC の長さを表す。

接線どうしの交点を求める

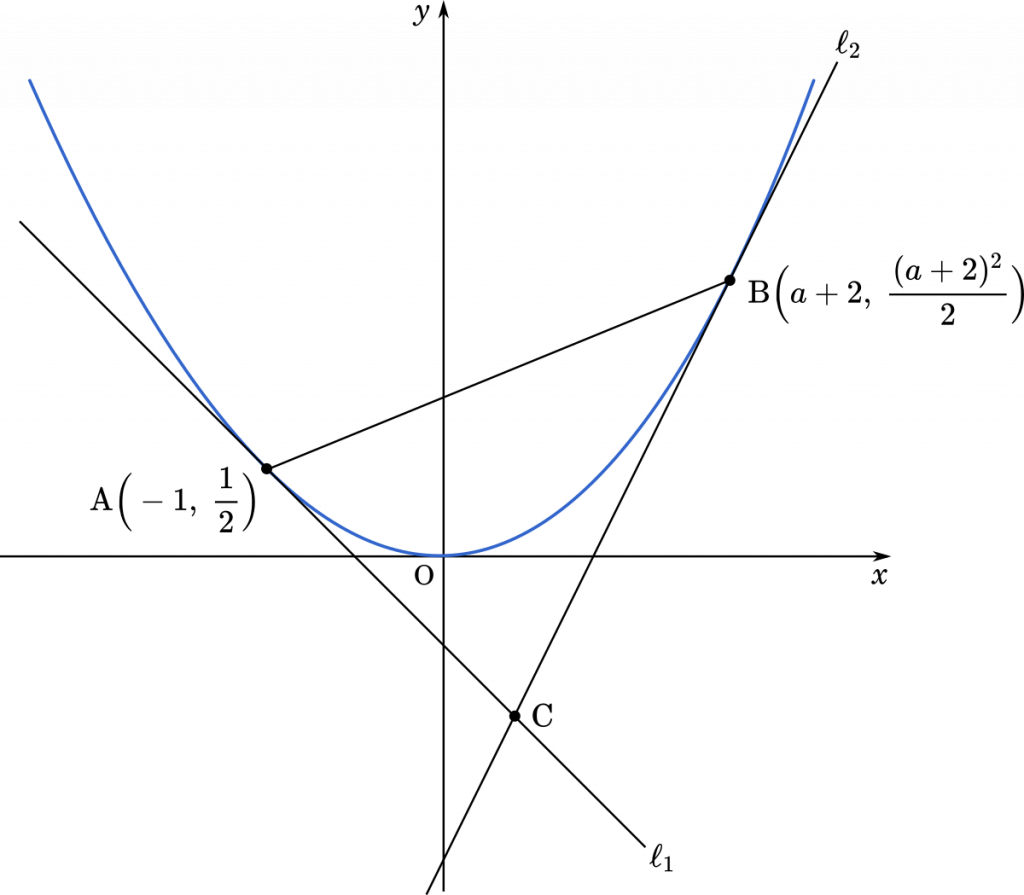
接線が２本あるので，まずは接線の方程式から作っていきましょう。

考え方としては，二次関数を微分して接線の傾きを求め，平行移動して接線の方程式を作ります。

$y=\cfrac{1}{2}x^2$ を微分します

$y’=x$

よって $x=-1$ のとき，$y’=-1$ だから

$\ell_1$ の方程式は

$y-\cfrac{1}{2}=(-1)(x+1)$
$y=-x-1+\cfrac{1}{2}$
$=-x-\cfrac{1}{2}$ ・・・①

次に，$x=a+2$ のとき，$y’=a+2$ だから

$\ell_2$ の方程式は

$y-\cfrac{(a+2)^2}{2}=(a+2)(x-a-2)$
$y=(a+2)x-(a+2)^2+\cfrac{(a+2)^2}{2}$

$y=(a+2)x-\cfrac{(a+2)^2}{2}$ ・・・②

①，②の交点を求めると

$-x-\cfrac{1}{2}=(a+2)x-\cfrac{(a+2)^2}{2}$
$(a+2)x+x=\cfrac{(a+2)^2}{2}-\cfrac{1}{2}$
$(a+3)x=\cfrac{a^2+4a+4-1}{2}$
$=\cfrac{a^2+4a+3}{2}$
$x=\cfrac{(a+1)(a+3)}{2(a+3)}$　$(a\not=-3)$
$=\cfrac{a+1}{2}$

①に代入して

$y=-\cfrac{a+1}{2}-\cfrac{1}{2}$
$=-\cfrac{a+2}{2}$

したがって，点 C の座標は

$\text{C}\Big(\cfrac{a+1}{2},\space-\cfrac{a+2}{2}\Big)$　（答え）

辺の長さの比を求める

(2)に進みます。

AB の長さを求めるには，B の座標から A の座標を引き算した上で，三平方の定理に持ち込みます。

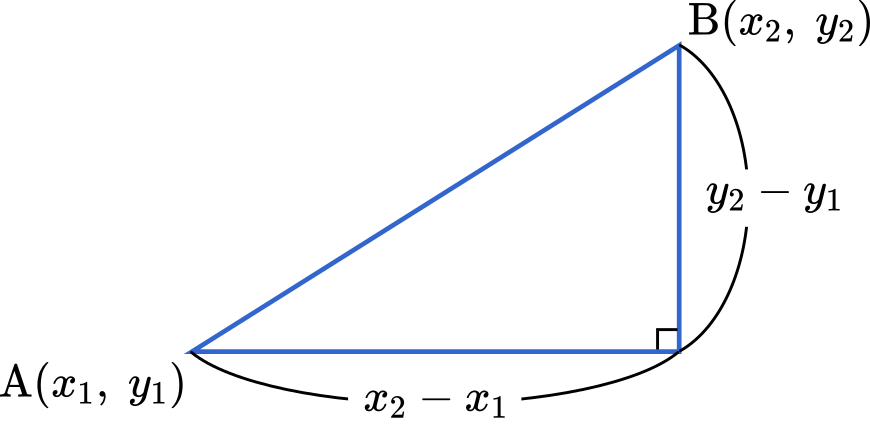
三平方の定理を用いて

$|\text{AB}|^2=(a+2+1)^2+\Big\{\cfrac{(a+2)^2}{2}-\cfrac{1}{2}\Big\}^2$
$=(a+3)^2+\Big(\cfrac{a^2+4a+4-1}{2}\Big)^2$
$=(a+3)^2+\Big(\cfrac{a^2+4a+3}{2}\Big)^2$
$=(a+3)^2+\Big\{\cfrac{(a+1)(a+3)}{2}\Big\}^2$
$=(a+3)^2+\cfrac{(a+1)^2(a+3)^2}{4}$

$=(a+3)^2\Big\{1+\cfrac{(a+1)^2}{4}\Big\}$
$=\cfrac{(a+3)^2}{4}\{4+(a+1)^2\}$ ・・・③

また

$|\text{BC}|^2=\Big(\cfrac{a+1}{2}-a-2\Big)^2+\Big(-\cfrac{a+2}{2}-\cfrac{(a+2)^2}{2}\Big)^2$
$=\Big(-\cfrac{a+3}{2}\Big)^2+\Big(\cfrac{-a-2-a^2-4a-4}{2}\Big)^2$
$=\Big(-\cfrac{a+3}{2}\Big)^2+\Big(-\cfrac{a^2+5a+6}{2}\Big)^2$
$=\cfrac{1}{4}(a+3)^2+\cfrac{1}{4}(a^2+5a+6)^2$
$=\cfrac{1}{4}(a+3)^2+\cfrac{1}{4}\{(a+2)(a+3)\}^2$
$=\cfrac{1}{4}(a+3)^2+\cfrac{1}{4}(a+2)^2(a+3)^2$

$=\cfrac{(a+3)^2}{4}\{1+(a+2)^2\}$ ・・・④

最終的に求めないといけないのは，$\cfrac{|\text{AB}|}{|\text{BC}|}$ の最小値でした。③，④を使って，$\cfrac{|\text{AB}|^2}{|\text{BC}|^2}$ の最小値を求めます。

$\cfrac{|\text{AB}|^2}{|\text{BC}|^2}=\cfrac{\cfrac{(a+3)^2}{4}\{4+(a+1)^2\}}{\cfrac{(a+3)^2}{4}\{1+(a+2)^2\}}$

$=\cfrac{4+(a+1)^2}{1+(a+2)^2}$
$=\cfrac{a^2+2a+5}{a^2+4a+5}$

ここから，分母か分子の $a$ を消去できれば最小値を考えることができます。

$=\cfrac{a^2+4a+5-2a}{a^2+4a+5}$
$=1-\cfrac{2a}{a^2+4a+5}$
$=1-\cfrac{2}{a+4+\cfrac{5}{a}}$

相加・相乗平均より

$a+\cfrac{5}{a}\geqq2\sqrt{a\cdot\cfrac{5}{a}}$
$a+\cfrac{5}{a}\geqq2\sqrt{5}$

ここで，$a+\cfrac{5}{a}$ が最小のときに，$\cfrac{2}{a+4+\cfrac{5}{a}}$ が最大となり,$1-\cfrac{2}{a+4+\cfrac{5}{a}}$ は最小となります。

等号成立は，$a=\cfrac{5}{a}$ のときだから

$a^2=5$
$a=\pm\sqrt{5}$

$a>0$ より

$a=\sqrt{5}$

したがって，$\cfrac{|\text{AB}|}{|\text{BC}|}$ の最小値は $a=\sqrt{5}$ のとき。（答え）