【IIB微分・ベクトル】二次関数の接線－解と係数の関係を使い倒して式を整理する(東京都立大2016理系第3問)

$a$ と $b$ は $a^2>b$ をみたす実数であるとする。座標平面上において，点 P($a,b$) から曲線 $y=x^2$ に引いた 2 つの接線の接点をそれぞれ Q，R とする。以下の問いに答えなさい。（東京都立大2016）

(1) 内積 $\overrightarrow{\text{PQ}}\cdot\overrightarrow{\text{PR}}$ を $a$ と $b$ の式で表しなさい。

(2) 三角形 PQR の面積 S を $a$ と $b$ の式で表しなさい。

(3) 直線 $y=2x-3$ を $\ell$ とする。点 P が $\ell$ 上を動くとき，(2)の $S$ の最小値を求めなさい。

解と係数の関係を利用する

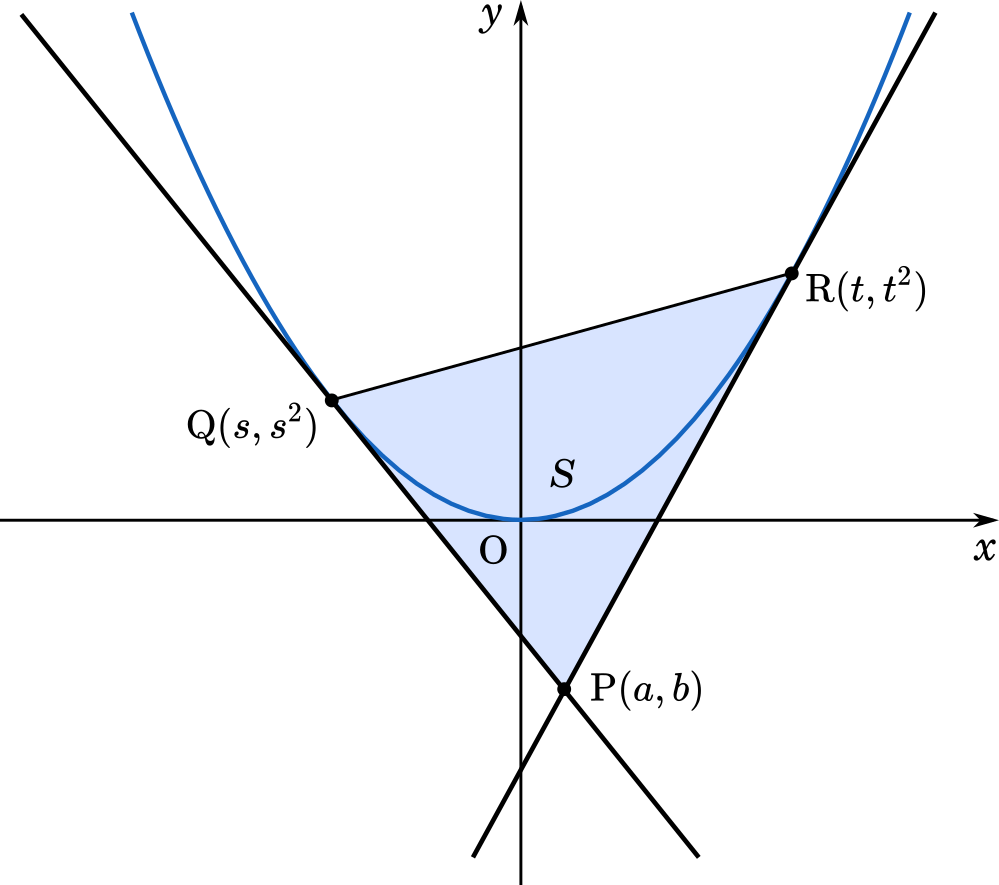
(1)から始めます。

まず，接線の式を作りましょう。

$y=x^2$ 上の点 $(k,k^2)$ を通る接線の傾きは，$y’=2x$ より $2k$ となる。

接線の式は

$y-k^2=2k(x-k)$
$y=2kx-k^2$

これが，$(a,b)$ を通るから

$b=2ak-k^2$
$k^2-2ak+b=0$　・・・①

$k=a\pm\sqrt{a^2-b}$

接線は 2 本引くことができるので，$k$ の値も 2 個あります。

よって

$\overrightarrow{\text{PQ}}=(a-\sqrt{a^2-b}-a,(a-\sqrt{a^2-b})^2-b)$
$\overrightarrow{\text{PR}}=(a+\sqrt{a^2-b}-a,(a+\sqrt{a^2-b})^2-b)$

そこで，いったん
$s=a-\sqrt{a^2-b}$
$t=a+\sqrt{a^2-b}$

とおいて

点 Q$(s,s^2)$，R$(t,t^2)$ として計算してみます。

①の解を $s,t$ として，解と係数の関係を用いると

$s+t=2a$，$st=b$

$\overrightarrow{\text{PQ}}\cdot\overrightarrow{\text{PR}}=(s-a)(t-a)+(s^2-b)(t^2-b)$
$=st-(s+t)a+a^2+(st)^2-(s^2+t^2)b+b^2$
$=b-2a^2+a^2+b^2-(s^2+t^2)b+b^2$

ここで

$(s+t)^2=s^2+2st+t^2$
$s^2+t^2=(s+t)^2-2st$
$=(2a)^2-2b$
$=4a^2-2b$

よって

$=b-a^2+b^2-(4a^2-2b)b+b^2$
$=b-a^2+b^2-4a^2b+2b^2+b^2$
$=-a^2-4a^2b+4b^2+b$

もう少し式を整理しましょう。

$=-(1+4b)a^2+(4b+1)b$
$=(1+4b)(b-a^2)$　（答え）

三角形の面積を求める

(2)に進みます。

ベクトルを用いた三角形の面積を求めるときには公式があるのですが

$S=\cfrac{1}{2}\sqrt{|\vec{a}|^2|\vec{b}|^2-(\vec{a}\cdot\vec{b})^2}$

これを使うとかえって計算がやっかいになります。そこで，原点と 2 点を結ぶ三角形の面積の公式を使いましょう。

これを用いて

$S=\cfrac{1}{2}|(s-a)(t^2-b)-(s^2-b)(t-a)|$
$=\cfrac{1}{2}|st^2-bs-at^2+ab-s^2t+as^2+bt-ab|$
$=\cfrac{1}{2}|st(t-s)+a(s^2-t^2)+b(t-s)|$
$=\cfrac{1}{2}|st(t-s)+a(s+t)(s-t)+b(t-s)|$
$=\cfrac{1}{2}|st(t-s)-a(s+t)(t-s)+b(t-s)|$

$t>s$ より $t-s>0$ だから

$=\cfrac{1}{2}(t-s)|st-a(s+t)+b|$

$s+t=2a$，$st=b$ だったので

$=\cfrac{1}{2}(t-s)|b-2a^2+b|$
$=\cfrac{1}{2}(t-s)|2b-2a^2|$
$=(t-s)|b-a^2|$

問題文より，$a^2>b$ だったので，絶対値の中はマイナスになります。そこで，符号を逆にして絶対値を外しましょう。

$=(t-s)(a^2-b)$

ここで

$s=a-\sqrt{a^2-b}$
$t=a+\sqrt{a^2-b}$

だったので

$t-s=2\sqrt{a^2-b}$

よって

$=2\sqrt{a^2-b}(a^2-b)$
$=2(a^2-b)^{\small{\frac{3}{2}}}$　（答え）

解答としては　$2\sqrt{a^2-b}(a^2-b)$ と
$2(a^2-b)^{\small{\frac{3}{2}}}$ はどちらでも構いません。

面積の最大値を求める

(3)に進みますが，ここはすぐに終わります。

P$(k,2k-3)$ とすると

$S=2(k^2-2k+3)^{\small{\frac{3}{2}}}$

結果的に，$k^2-2k+3$ の最小値を求めればよいことになります。

$f(k)=k^2-2k+3$ とすると，式を平方完成して

$=(k-1)^2+2$

よって $k^2-2k+3$ は $k=1$ のときに最小値 2 をとるので

$S=2\cdot2^{\small{\frac{3}{2}}}$
$=2\cdot\sqrt{2^3}$
$=2\cdot2\sqrt{2}$
$=4\sqrt{2}$　（答え）