内積一定のまま回転するベクトルが作る図形(横浜国立大2017理系第3問)
空間に 2 つの定点 O,A があり,$|\overrightarrow{\text{OA}}|=2$ をみたしている。また,2 点 P,Q は次の条件をみたしながら動く。
$|\overrightarrow{\text{OP}}|\leqq5$,$\overrightarrow{\text{OP}}\cdot\overrightarrow{\text{OA}}=6$
$|\overrightarrow{\text{OQ}}|=\sqrt{5}$,$\overrightarrow{\text{OQ}}\cdot\overrightarrow{\text{OA}}=-2$
ただし,$\overrightarrow{\text{OP}}\cdot\overrightarrow{\text{OA}}$ は $\overrightarrow{\text{OP}}$ と $\overrightarrow{\text{OA}}$ の内積を表す。次の問いに答えよ。
(1) $|\overrightarrow{\text{OP}}|$ の最小値を求めよ。
(2) $|\overrightarrow{\text{PQ}}|$ のとり得る値の範囲を求めよ。
(3) 線分 PQ が通過してできる部分の体積を求めよ。
内積の公式を用いる
(1)から始めます。ここは内積の公式を用いて考えていきます。
$\overrightarrow{\text{OP}}\cdot\overrightarrow{\text{OA}}=|\overrightarrow{\text{OP}}||\overrightarrow{\text{OA}}|\cos\theta$ とすると
$|\overrightarrow{\text{OP}}|\cdot2\cos\theta=6$
$|\overrightarrow{\text{OP}}|=\cfrac{3}{\cos\theta}$
$0\leqq\cos\theta\leqq1$ より,$|\overrightarrow{\text{OP}}|$ は $\cos\theta=1$ のとき,最小値 3 をとる。(答え)

点 A を固定して考える
(2)に進みます。

点 P,Q は A との内積が示されています。これは $\overrightarrow{\text{OA}}$ を基準とすれば,P,Q の相対的な位置関係が決まってくる,と解釈できます。
しかし,点 A の場所が決まっていないので,P と Q の場所はなおさら分かりません。

そこで,点 A をいったん固定してみます。このとき,A はどこに固定しても構いません。P,Q の相対的な位置関係さえ分かれば,$|\overrightarrow{\text{PQ}}|$ を求めることができるからです。
$\overrightarrow{\text{OA}}$ は長さが 2 だから,計算がラクになるように A$(2,0,0)$ としてみましょう。
A$(2,0,0)$
P$(x_1,y_1,z_1)$
Q$(x_2,y_2,z_2)$
として
$\overrightarrow{\text{OQ}}$ の方が長さが決まっているので,こちらから考えましょう。
$\overrightarrow{\text{OA}}\cdot\overrightarrow{\text{OQ}}=2x_2+0\cdot y_2+0\cdot z_2=-2$ より
$x_2=-1$
よって
$|\overrightarrow{\text{OQ}}|^2={x_2}^2+{y_2}^2+{z_2}^2=5$ より
$(-1)^2+{y_2}^2+{z_2}^2=5$
${y_2}^2+{z_2}^2=4$
これは円の方程式です。点 Q は,中心の座標 $(-1,0,0)$,半径 2 で $x$ 軸に垂直な円の周上の点となります。
同様に
$\overrightarrow{\text{OA}}\cdot\overrightarrow{\text{OP}}=2x_1=6$
$x_1=3$
よって
$|\overrightarrow{\text{OP}}|^2=3^2+{y_1}^2+{z_1}^2$
また,(1)より
$3\leqq|\overrightarrow{\text{OP}}|\leqq5$ だから
$9\leqq|\overrightarrow{\text{OP}}|^2\leqq25$
$9\leqq9+{y_1}^2+{z_1}^2\leqq25$
$0\leqq{y_1}^2+{z_1}^2\leqq16$
点 P は,中心の座標 $(3,0,0)$,半径 0 から 4 間で $x$ 軸に垂直な円の周上の点となります。
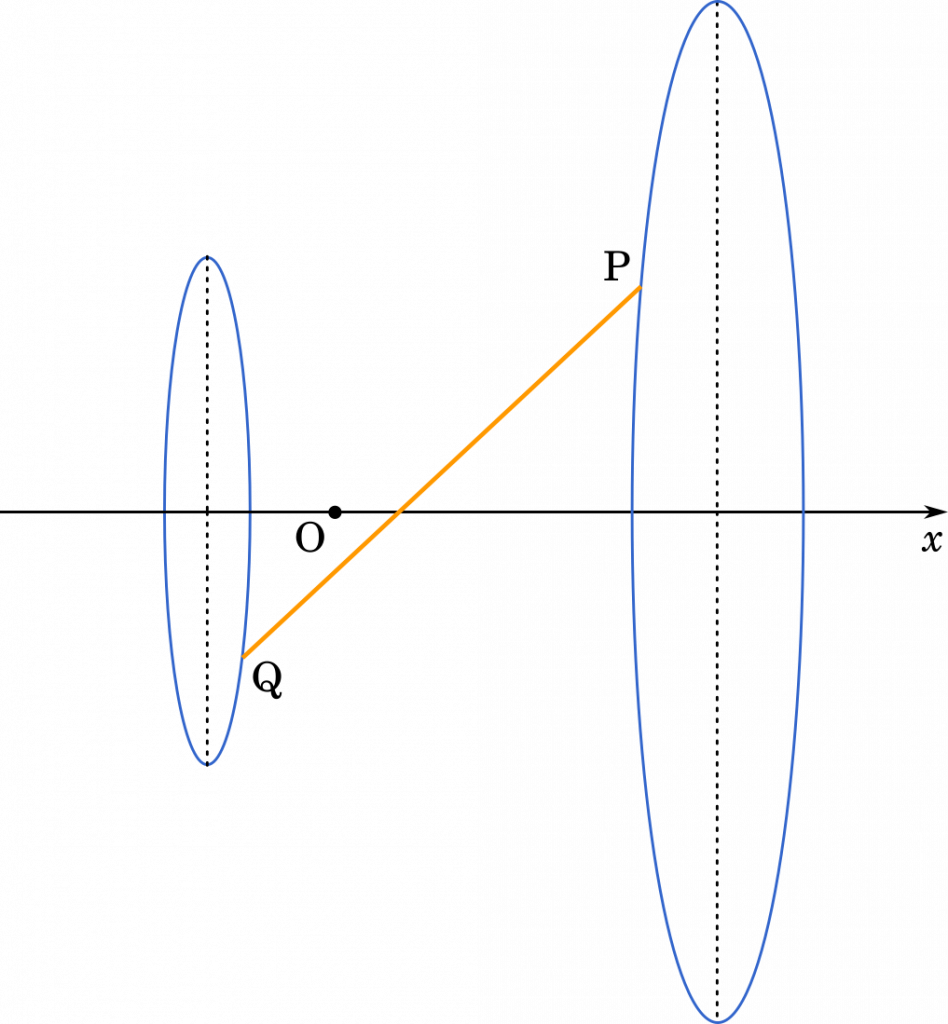
イメージとしては上のような感じです。ここから,$|\text{PQ}|$ の最小と最大を考えてみます。
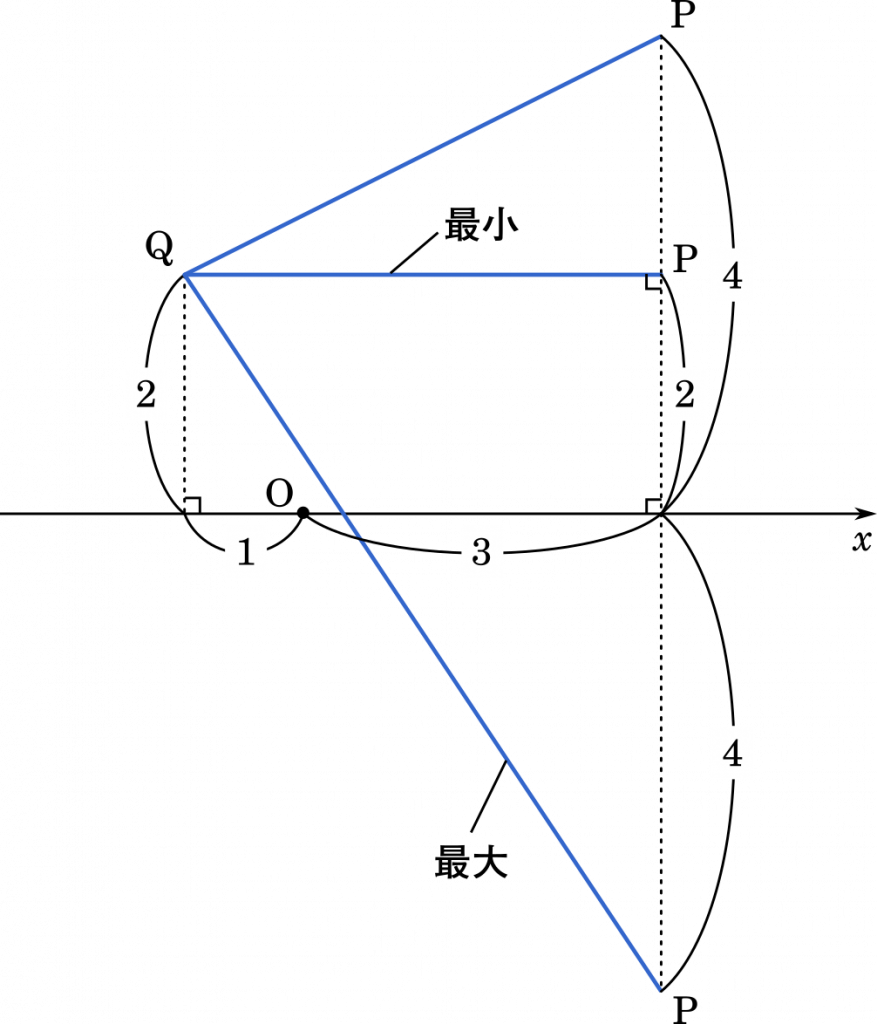
実際に図を描いてみると,最小と最大が見えてきます。
最小は 4
最大は,三平方の定理より
$\sqrt{4^2+6^2}$
$=\sqrt{52}$
$=2\sqrt{13}$
したがって,$|\overrightarrow{\text{PQ}}|$ のとり得る値の範囲は
$4\leqq|\overrightarrow{\text{PQ}}|\leqq2\sqrt{13}$ (答え)
回転体の体積を求める
(3)に進みます。
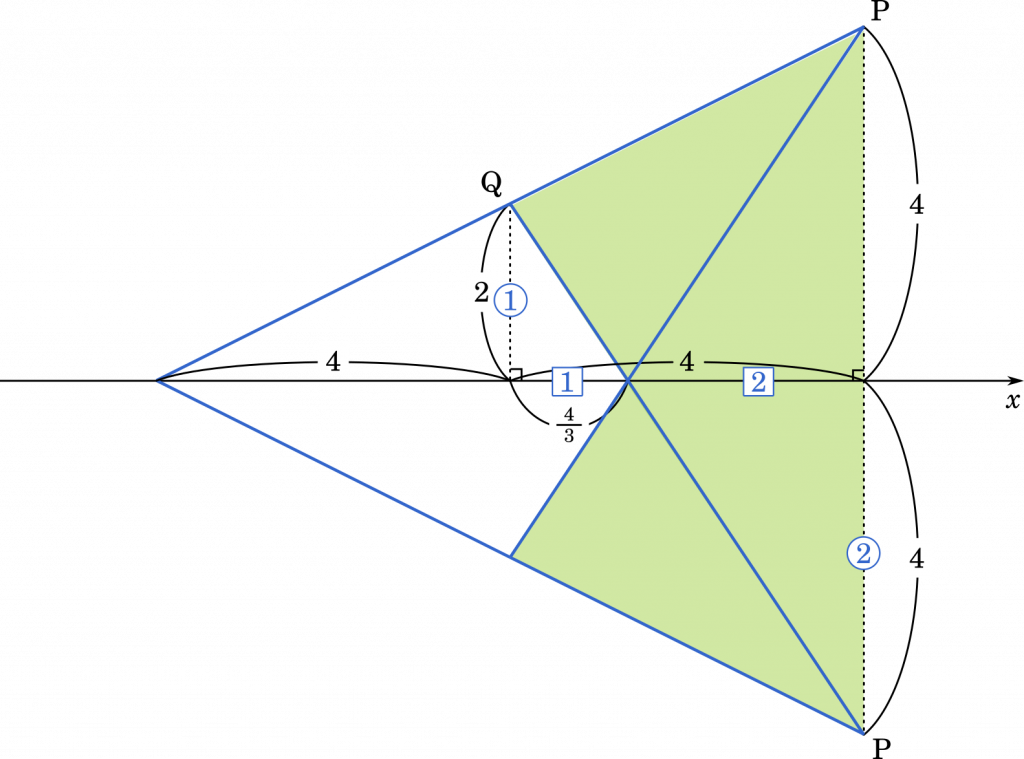
点 P が存在する円の半径を 0 から 4 まで変化させたとき,直線 PQ が通過してできる部分は上の緑色の部分です。
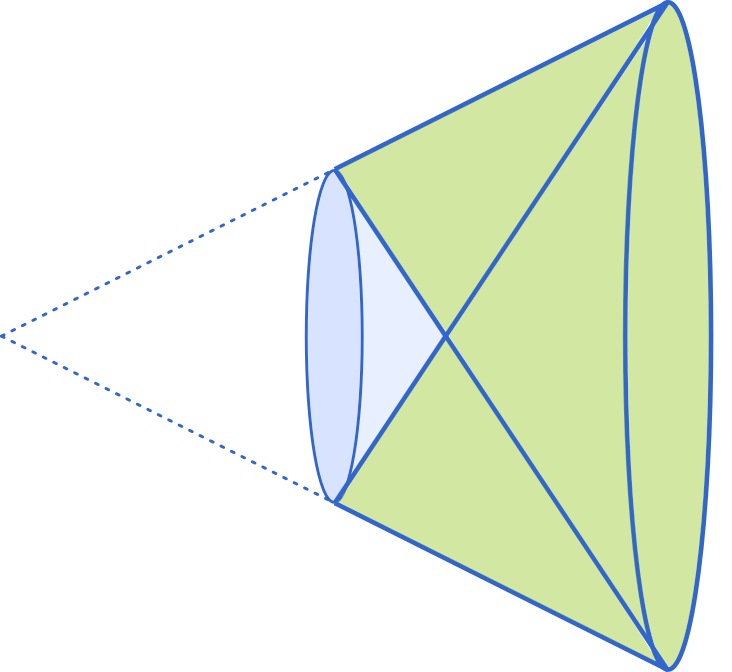
これを立体で考えると,PQ が通過してできる部分は上のように,大きな円錐から小さな円錐を 2 つ引いた残りです。
したがって
$V=\cfrac{1}{3}\cdot4^2\pi\cdot8-\cfrac{1}{3}\cdot2^2\pi\cdot4-\cfrac{1}{3}\cdot2^2\pi\cdot\cfrac{4}{3}$
$=\cfrac{\pi}{3}\Big(128-16-\cfrac{16}{3}\Big)$
$=\cfrac{\pi}{3}\cdot\cfrac{320}{3}$
$=\cfrac{320}{9}\pi$ (答え)
SNSでシェア