【数Ⅱ軌跡と領域】領域はタテ方向で考える　線形計画法における最大・最小の求め方

領域の問題で、最大・最小を求めるヤツが分からないです。というか領域の取り方が分からない。

まずは領域の作りかたをマスター

まずは領域の作りかたから復習していきます。

$x\text≧ 0,y\text≧ 0$は以下のようになります。

ここは分かります。

次に$x+3y\text≦ 15$の領域はこうなる。

そうそう、ここで分からなくなった。どっちを塗っていいか分かんなくなる。

ここがつまづきやすいポイントです。

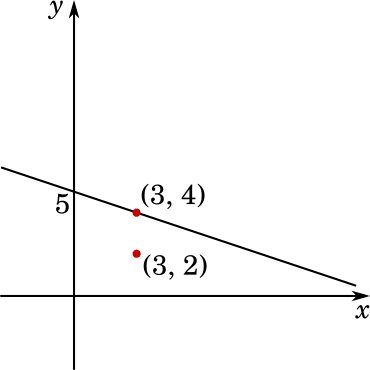
$x+3y\text≦ 15$を変形すると$\displaystyle y\text≦ -\frac{1}{3}x+5$となります。

このとき、例えば$x$が$3$だったとしましょう。このとき$y$の値は$\displaystyle -\frac{1}{3}\cdot3+5=4$になります。

これは点$(3,4)$ということになります。

このとき、また別に例えば$x$は$3$で$y$は$2$という点があったとします。

$y$の値が小さい点は、下の方向に移動することになります。

はあ？

つまり、こういうこと。

了解です！

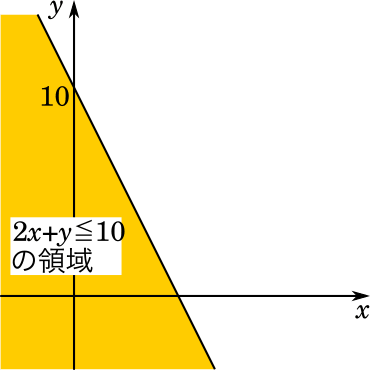
また、$2x+y\text≦ 10$の領域はこうなります。

全部を重ねると、領域$D$はこうなる。

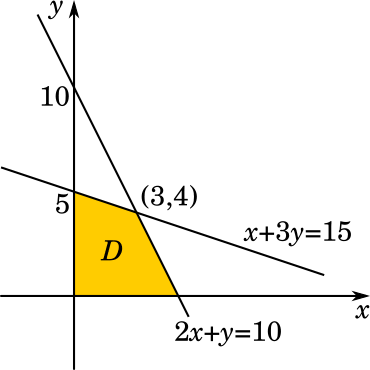
数字をいったん固定するためにkを用いる

ここで、$3x+2y=k$とします。

それそれ、そこが一番分からない。なんで$k$にするの？

$3x+2y$の最大値を求めろって言われても、実際$x$と$y$にはどんな数でも入るじゃない？

何でもいいんだ。

だけど、ホントは何でもいいワケじゃない。例えば、点$(4,9)$だと領域$D$の外側になってしまう。でも、点$(1,1)$なら領域の中に入るからオッケーだよね？

どこでもいいわけじゃないんだ。

領域$D$上の点じゃないとダメなの。

でも、どこでオッケーなのかが分からないですよ。

ここで、例えば$3x+2y$が$1$だとしましょう。式変形すると$\displaystyle y=-\frac{3}{2}x+\frac{1}{2}$になります。これをグラフで表すと次のようになります。

このとき、$\displaystyle y=-\frac{3}{2}x+\frac{1}{2}$は、もともと$3x+2y=1$だったので、この直線上の点はどこでも1になります。

そうすると、領域$D$と重なる範囲が絞られてきます。$\displaystyle 0\text≦ x\text≦ \frac{1}{3},0\text≦ y \text≦ \frac{1}{2}$のときに領域$D$と重なります。このようにして、いったん$x$と$y$の範囲を絞っていきます。

k がいろいろな値になるケースを考える

さらにここから、$3x+2y$が色んな数になる場合を考えてみましょう。

こう考えてみると、領域$D$と重ならないヤツがでてくるよね。

20のときとかアウトです。

そういうこと。こうやって見てみると$3x+2y$は$0$から$17$の間じゃないといけないよね。つまり、

最大値は17、最小値は0…(答え)

となる。

こうやって、色んなケースを考えていくから、$3x+2y=k$として、$k$に色んな数を当てはめて考えてみようってことなの。

最大・最小を式で表す

実際の証明の進め方はこうなります。

最大値を求める。

$3x+2y=k$として、

$\displaystyle y=-\frac{3}{2}x+\frac{1}{2}k$

点$(3,4)$を通るので、

$\displaystyle 4=-\frac{3}{2}\cdot3+\frac{1}{2}k$

より

$k=17$

最小値を求める。

$3x+2y=k$は点$(0,0)$を通るので、

$\displaystyle 0=-\frac{3}{2}\cdot 0+\frac{1}{2}k$より

$k=0$

答え出た。

この問題って、実際に図を書いてみないと分からないから必ず図を書いてみてね。そのあと直線を引いてみて、どこが領域の端になるかを考えるとうまくいくから。