【数III微分積分】関数の絶対値の積分(北海道大2017)

関数 $f(x)=1+\sin x-x\cos x$ について，以下の問いに答えよ。(北海道大2017)

(1) $f(x)$ の $0\leqq x\leqq 2\pi$ における増減を調べ，最大値と最小値を求めよ。

(2) $f(x)$ の不定積分を求めよ。

(3) 次の定積分の値を求めよ。

$\displaystyle\int_0^{2\pi}|f(x)|dx$

増減表を作る

(1)から始めます。

ここは，素直に微分して増減表を作っていきましょう。$x\cos x$ の部分は積の微分の公式を使います。

$f'(x)=\cos x-\{x’\cos x+x(\cos x)’\}$
$=\cos x-\cos+x\sin x$
$=x\sin x$

$x\sin x=0$ のとき
$x=0$ または $\sin x=0$

$\sin x=0$ のとき，$0\leqq x\leqq 2\pi$ に注意して
$x=0,\pi,2\pi$

増減表は

$\def\arraystretch{1.25}\begin{array}{|c||c|c|c|c|c|}\hline x&0&\cdots&\pi&\cdots&2\pi\\\hline f'(x)&0&+&0&-&0\\\hline f(x)&1&\nearrow&1+\pi&\searrow&1-2\pi\\\hline\end{array}$

$f(0)=1+\sin0-0\cos0=1$
$f(\pi)=1+\sin\pi-\pi\cos\pi$
$=1+0+\pi=1+\pi$
$f(2\pi)=1+\sin2\pi-2\pi\cos2\pi$
$=1+0-2\pi\cdot1=1-2\pi$

(答え)

三角関数の不定積分

(2)に進みます。

今度は積分ですが，$x\cos x$ の部分は部分積分を用います。

$x\cos x$ の部分について積分してみましょう。

$\displaystyle\int x\cos x\enspace dx$
$\displaystyle=\int x(\sin x)’dx$
$\displaystyle=x\sin x-\int x’\sin x\enspace dx$
$\displaystyle=x\sin x-\int\sin x\enspace dx$
$=x\sin x-(-\cos x)$
$=x\sin x+\cos x$

となります。したがって

$F(x)=x-\cos x-x\sin x-\cos x+C$
$=x-x\sin x-2\cos x+C$

($C$は積分定数)　(答え)

未知の解を求める

(3)に進みます。

(1)で求めた増減表から，$y=f(x)$ と $y=|f(x)|$ のグラフはこうなります。

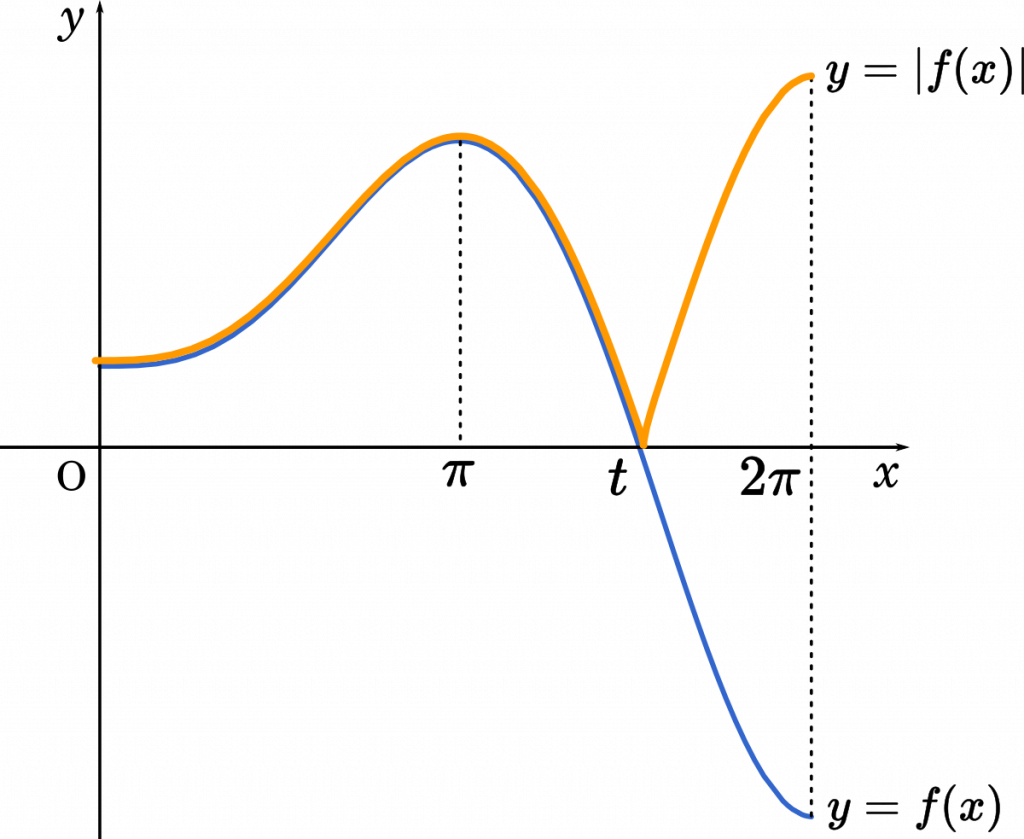
実際に試験問題を解いているときは，グラフの形はざっくりしたもので大丈夫です。

気を付けるべき点は，関数が絶対値のとき，$x$ 軸の下の部分をひっくり返すことです。

こうして，実際にグラフを描いてみると積分区間を 2 つに分ける必要があることが分かります。上のグラフでは区間を分ける点をとりあえず $t$ としています。実際に $t$ を求めてみましょう。

$f(t)=1+\sin t-t\cos t=0$ とおく

先ほどのグラフで考えると $t$ の範囲は，$\pi<t<2\pi$ です。この範囲では，$\sin t$ はマイナスで，$\cos t$ はプラスとマイナスの両方があります。

この方程式は結局，式変形によって解くことができません。しかし，$\pi<t<2\pi$ の範囲でいろいろ数を当てはめてみると $t=\cfrac{3}{2}\pi$ のとき，たまたま式が 0 になることを発見できます。

$f\Big(\cfrac{3}{2}\pi\Big)=1+(-1)-\cfrac{3}{2}\pi\cdot0=0$

よって

$t=\cfrac{3}{2}\pi$

おそらくここで出題者が要求していることは，偶然成り立つに過ぎない法則を発見する能力です。

一見するとただの意地悪問題のように思えるかもしれません。しかし，出題者の意図はそれではないと思います。

私たちが何かの問題に取り組むとき，既に分かっている法則だけを利用する限り，その組み合わせによって得られる解のパターンは有限です。しかし，現実の世界ではその有限のパターンの外側に解が存在することがあり得るのです。ノーベル賞を受賞するような科学的発見も，そうした偶然の中から発見されることも多いのです。

$t=\cfrac{3}{2}\pi$ がたまたま発見された結果に過ぎないとしても，方程式が成り立つ限り，それは科学的思考として正当なものであると言えるのです。

(2)の結果を利用して

$\displaystyle S=\int_0^{\large{\frac{3}{2}\pi}}f(x)dx-\int_{\large{\frac{3}{2}\pi}}^{2\pi}f(x)dx$
$\displaystyle=\Big[x-x\sin x-2\cos x\Big]_0^{\large{\frac{3}{2}\pi}}-\big[x-x\sin x-2\cos x\Big]_{\large{\frac{3}{2}\pi}}^{2\pi}$
$=\cfrac{3}{2}\pi-\cfrac{3}{2}\pi(-1)-2\cdot0-0+0\cdot0+2\cdot1-\Big\{2\pi-2\pi\cdot0-2\cdot1-\Big(\cfrac{3}{2}\pi-\cfrac{3}{2}\pi(-1)-2\cdot0\Big)\Big\}$
$=\cfrac{3}{2}\pi+\cfrac{3}{2}\pi+2-2\pi+2+\cfrac{3}{2}\pi+\cfrac{3}{2}\pi$
$=6\pi+4-2\pi$
$=4+4\pi$ (答え)