【数Ⅲ複素数平面】z の n 乗根の方程式 解き方と考え方
問題 方程式 $z^4=-8+8\sqrt{3}$ を解け。

1のn乗根のやり方はマスターした?

一応、分かってるかと。

分かってなかったら1のn乗根の解き方に戻ってね。今回は、それが分かってる前提でやっていくよ。
式を極形式で表す

まず、式を極形式で表す。8でくくれそうだからいっぺんカッコをつける。
$z^4=-8+8\sqrt{3}$
$z^4=8(-1+\sqrt{3}i)$
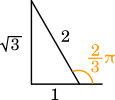

複素平面上で $-1+\sqrt{3}i$ の点ってこんな感じなるから、長さが $2$ で偏角は $\displaystyle\frac{2}{3}\pi$ になる。これを極形式で表す。
$\displaystyle z^4=8\cdot 2\left(\cos\frac{2}{3}\pi+i\sin\frac{2}{3}\pi\right)$

極形式なおすのが難しいです。

ここは引っかかりやすいところだから、上でやったように最初は三角形書いてみるといいよ。長さが2になるから、2をかけるのも忘れずにね。
$\displaystyle z^4=16\left(\cos\frac{2}{3}\pi+i\sin\frac{2}{3}\pi\right)\cdots$①

そして、求める $z$ を長さ $r$、偏角 $\theta$ として仮の形として表しておく。
$z=r(\cos\theta+i\sin\theta)$ とおくと
$z^4=r^4(\cos\theta+i\sin\theta)^4$
ド・モアブルの定理より
$z^4=r^4(\cos 4\theta+i\sin 4\theta)\cdots$②
①、②の係数を比べると
$\displaystyle r^4=16$、$\displaystyle 4\theta=\frac{2}{3}\pi+2k\pi$

$r$ は長さだからマイナスの数になることはない。あと、$+2k\pi$ ってのはぐるっと1周回って同じところに戻ってくるヤツで、n乗根を求めるときにはこれも考慮する必要があった。
$r=2$、$\displaystyle \theta=\frac{\pi}{6}+\frac{k\pi}{2}$
よって
$\displaystyle z=2\left\{\cos\left(\frac{\pi}{6}+\frac{k\pi}{2}\right)+i\sin\left(\frac{\pi}{6}+\frac{k\pi}{2}\right)\right\}$
$0\leqq\theta<2\pi$ の範囲では、$k=0,1,2,3$

4乗根を求めるなら、解は4つ出てくる。
したがって
$\displaystyle z_0=2\left(\cos\frac{\pi}{6}+i\sin\frac{\pi}{6}\right)=2\left(\frac{\sqrt{3}}{2}+\frac{1}{2}i\right)=\sqrt{3}+i$
$\displaystyle z_1=2\left\{\cos\left(\frac{\pi}{6}+\frac{\pi}{2}\right)+i\sin\left(\frac{\pi}{6}+\frac{\pi}{2}\right)\right\}=2\left(-\frac{1}{2}+\frac{\sqrt{3}}{2}i\right)=-1+\sqrt{3}i$
$\displaystyle z_2=2\left\{\cos\left(\frac{\pi}{6}+\pi\right)+i\sin\left(\frac{\pi}{6}+\pi\right)\right\}=2\left(-\frac{\sqrt{3}}{2}-\frac{1}{2}i\right)=-\sqrt{3}-i$
$\displaystyle z_3=2\left\{\cos\left(\frac{\pi}{6}+\frac{3\pi}{2}\right)+i\sin\left(\frac{\pi}{6}+\frac{3\pi}{2}\right)i\right\}=2\left(\frac{1}{2}-\frac{\sqrt{3}}{2}i\right)=1-\sqrt{3}i$

計算の手順は決まりきったものだから、暗記で突破する問題。覚えるまで何度も見直すように。
SNSでシェア