【数III微分積分】x 以外の文字で微分するとき/回転体の体積(千葉大2012第11問)
$xy$ 平面において,長さ 1 の線分 AB を点 A が原点,点 B が点 (1,0) に重なるように置く。点 A を $y$ 軸に沿って点 (0,1) まで移動させ,線分 AB の長さを 1 に保ったまま点 B を $x$ 軸に沿って原点まで移動させる。このとき線分 AB が通る領域を $D$ とする。 0 ≦ $x$ ≦ 1 となる実数 $x$ に対して,点 $(x,y)$ が領域 D に含まれるような $y$ の最大値を $f(x)$ とする。
(1) $f(x)$ を $x$ の式で表せ。
(2) 領域 $D$ を $x$ 軸を中心に回転させた立体の体積 $V$ を求めよ。
x 以外の関数として微分する
(1)から進めます。
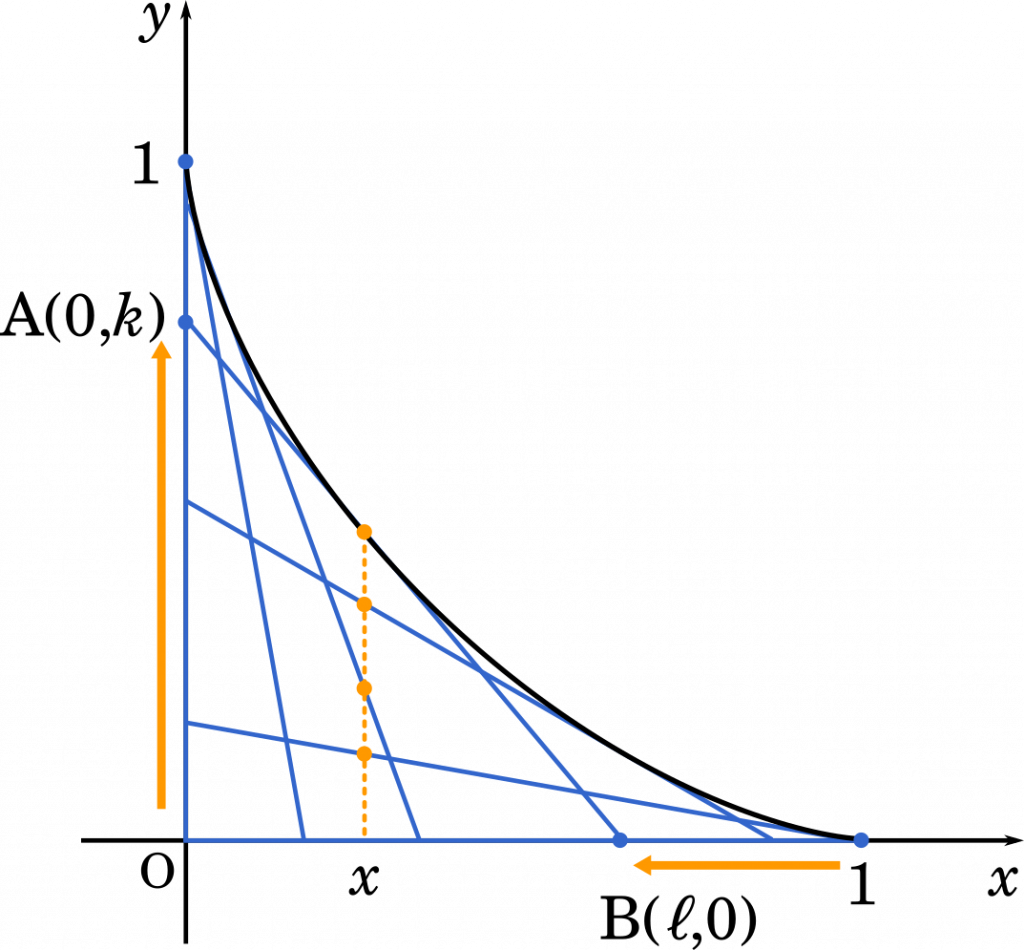
上の図のように,ある $x$ 座標における直線 AB の $y$ 座標は,直線 AB が変化するにつれてさまざまな値をとります。そして,その中で $y$ の値が最大のものを $f(x)$ とすればよい,ということです。
$y$ 座標を求めるためには直線の式が必要なので,いったん A$(0,k)$,B$(\ell,0)$ とおいて考えてみます。
このとき,線分 AB の長さは 1 だから三平方の定理より
$k^2+\ell^2=1$
$\ell$ ≧ 0 だから,式を変形して
$\ell=\sqrt{1-k^2}$
直線の式は $y=ax+b$ の形なので,傾き $a$ と切片 $b$ を求めます。
A$(0,k)$,B$(\ell,0)$ より,直線の傾きは $-\cfrac{k}{\ell}$ と表すことができます。また,図より切片は $k$ となります。直線の式は
$y=-\cfrac{k}{\ell}\space x+k$
$=-\cfrac{k}{\sqrt{1-k^2}}\space x+k$
ここで考え方を切り替えます。ここではある $x$ の値における $y$ の値の変化を考えています。$x$ がある固定した値であるとすると,$k$ の値によって $y$ が変化することになります。



$y$ の最大値を考えようとしても,$k$ の式として考えると形が複雑です。そこで,$y$ の増減を確かめるために,式を $k$ で微分してみます。

$y=-xk(1-k^2)^{\small{-\frac{1}{2}}}+k$ ・・・①
ここで $k(1-k^2)^{\small{-\frac{1}{2}}}$ の部分はかけ算の微分です。公式を思い出しましょう。
積の微分 $\{f(x)g(x)\}’=f'(x)g(x)+f(x)g'(x)$
$\{k(1-k^2)^{\small{-\frac{1}{2}}}\}’$
$=k'(1-k^2)^{\small{-\frac{1}{2}}}+k\{(1-k^2)^{\small{-\frac{1}{2}}}\}’$
さらに,$(1-k^2)^{\small{-\frac{1}{2}}}$ は合成関数の微分になります。ここも公式を思い出しましょう。
合成関数の微分 $f'(g(x))=f'(g(x))\cdot g'(x)$
$=(1-k^2)^{\small{-\frac{1}{2}}}+k\cdot\Big\{-\cfrac{1}{2}(1-k^2)^{\small{-\frac{3}{2}}}\cdot(-2k)\Big\}$
$=(1-k^2)^{\small{-\frac{1}{2}}}+k^2(1-k^2)^{\small{-\frac{3}{2}}}$

$=\cfrac{1}{\sqrt{1-k^2}}+\cfrac{k^2}{(1-k^2)\sqrt{1-k^2}}$
$=\cfrac{1-k^2+k^2}{(1-k^2)\sqrt{1-k^2}}$
$=\cfrac{1}{(1-k^2)\sqrt{1-k^2}}$
$=(1-k^2)^{\small{-\frac{3}{2}}}$
となるので①を $k$ で微分すると
$\cfrac{dy}{dk}=-x(1-k^2)^{\small{-\frac{3}{2}}}+1$
最大値を求めようとしているので,極値を考えます。

ここで,$-x(1-k^2)^{\small{-\frac{3}{2}}}+1=0$ とすると
$x(1-k^2)^{\small{-\frac{3}{2}}}=1$
$x=(1-k^2)^{\small{\frac{3}{2}}}$
両辺を $\cfrac{2}{3}$ 乗して
$x^{\small{\frac{2}{3}}}=(1-k^2)^{\small{\frac{3}{2}\cdot\frac{2}{3}}}$
$x^{\small{\frac{2}{3}}}=1-k^2$
$k^2=1-x^{\small{\frac{2}{3}}}$
$k=(1-x^{\small{\frac{2}{3}}})^{\small{\frac{1}{2}}}$
つまり,①は $k=(1-x^{\small{\frac{2}{3}}})^{\small{\frac{1}{2}}}$ で極値をとる。
増減表は
$\def\arraystretch{1.25}\begin{array}{|c||c|c|c|c|c|c|}\hline k&0&\cdots&(1-x^{\small{\frac{2}{3}}})^{\small{\frac{1}{2}}}&\cdots&1\\\hline\frac{dy}{dk}&+&+&0&-&-\\\hline y&\nearrow&\nearrow&\text{最大}&\searrow&\searrow\\\hline\end{array}$
①を $y=k\{1-x(1-k^2)^{\small{-\frac{1}{2}}}\}$ として
$k=(1-x^{\small{\frac{2}{3}}})^{\small{\frac{1}{2}}}$ を代入すると
$y=(1-x^{\small{\frac{2}{3}}})^{\small{\frac{1}{2}}}\{1-x(1-1+x^{\small{\frac{2}{3}}})^{\small{-\frac{1}{2}}}\}$
$y=(1-x^{\small{\frac{2}{3}}})^{\small{\frac{1}{2}}}(1-x\cdot x^{\small{-\frac{1}{3}}})$
$y=(1-x^{\small{\frac{2}{3}}})^{\small{\frac{1}{2}}}(1-x^{\small{\frac{2}{3}}})$
$y=(1-x^{\small{\frac{2}{3}}})^{\small{\frac{3}{2}}}$ (答え)
回転体の体積を求める
(2)に進みます。
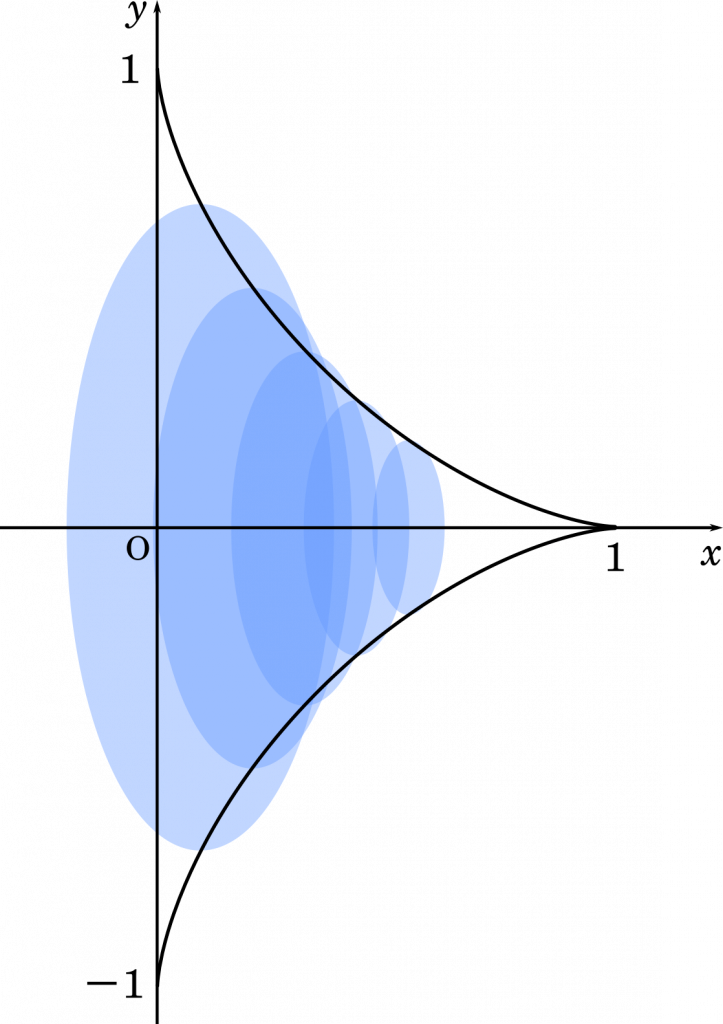
$x$ 軸を中心に回転させた体積は,図のように円の面積を重ねることで求めます。円の半径は $y$ 座標になるので面積は
$S=\pi y^2$
となります。これを $x$ 軸方向に積み重ねていくので,体積は
$\displaystyle V=\int_0^1 \pi y^2\space dx$
です。
$\displaystyle =\pi\int_0^1 \{(1-x^{\small{\frac{2}{3}}})^{\small{\frac{3}{2}}}\}^2\space dx$
$\displaystyle =\pi\int_0^1 (1-x^{\small{\frac{2}{3}}})^3\space dx$
3乗の公式を使って展開します。
$\displaystyle =\pi\int_0^1 1-3x^{\small{\frac{2}{3}}}+3x^{\small{\frac{2}{3}}\cdot2}-x^{\small{\frac{2}{3}}\cdot3} \space dx$
$\displaystyle =\pi\int_0^1 1-3x^{\small{\frac{2}{3}}}+3x^{\small{\frac{4}{3}}}-x^2 \space dx$
$\displaystyle =\pi\Big[x-3\cdot\cfrac{3}{5}x^{\small{\frac{5}{3}}}+3\cdot \cfrac{3}{7}x^{\small{\frac{7}{3}}}-\cfrac{x^3}{3}\Big]_0^1$
$=\pi\Big(1-\cfrac{9}{5}+\cfrac{9}{7}-\cfrac{1}{3}\Big)$
$=\cfrac{105-189+135-35}{105}\space\pi$
$=\cfrac{16}{105}\space\pi$ (答え)
SNSでシェア