【数III微分】直線の傾きの違いを利用した不等式の証明(北海道大2020理系第4問)

$\alpha$ を $0<\alpha<1$ を満たす実数とし，$f(x)=\sin\cfrac{\pi x}{2}$ とする。数列 $\{a_n\}$ が
$a_1=\alpha$，$a_{n+1}=f(a_n)$　$(n=1,2,\cdots)$
で定義されるとき，次の問に答えよ。（北海道大2020）

(1) すべての自然数 $n$ に対して，$0<a_n<1$ かつ $a_{n+1}>a_n$ が成り立つことを示せ。
(2) $b_n=\cfrac{1-a_{n+1}}{1-a_n}$ とおくとき，すべての自然数 $n$ に対して，$b_{n+1}<b_n$ が成り立つことを示せ。
(3) $\displaystyle\lim_{n\rightarrow\infty}a_n$ および(2)で定めた $\{b_n\}$ に対して $\displaystyle\lim_{n\rightarrow\infty}b_n$ を求めよ。

帰納法による証明

(1)から始めます。まず，$0<a_n<1$ は帰納法によって証明します。

$0<a_n<1$ ・・・(A)　とおく。
[I] $n=1$ のとき
$0<\alpha<1$ より $0<a_1<1$ だから，(A)は成り立つ。

[II] $n=k$ のとき，(A)が成り立つと仮定すると，$n=k+1$ のとき
$a_{k+1}=f(a_k)=\sin\cfrac{\pi a_k}{2}$
(A)が成り立つ，つまり $0<a_n<1$ のとき，$0<\sin\cfrac{\pi a_k}{2}<1$ だから，$0<a_{k+1}<1$ が成り立つ。

以上，[I]，[II] より，すべての自然数 $n$ において $0<a_n<1$ が成り立つ。（証明終わり）

直線の傾きをくらべる

次に，$a_{n+1}>a_n$ を証明します。まず，数列の形をつかむところから始めるとよいでしょう。

$a_1=\alpha$
$a_2=f(a_1)=\sin\cfrac{\pi a_1}{2}$

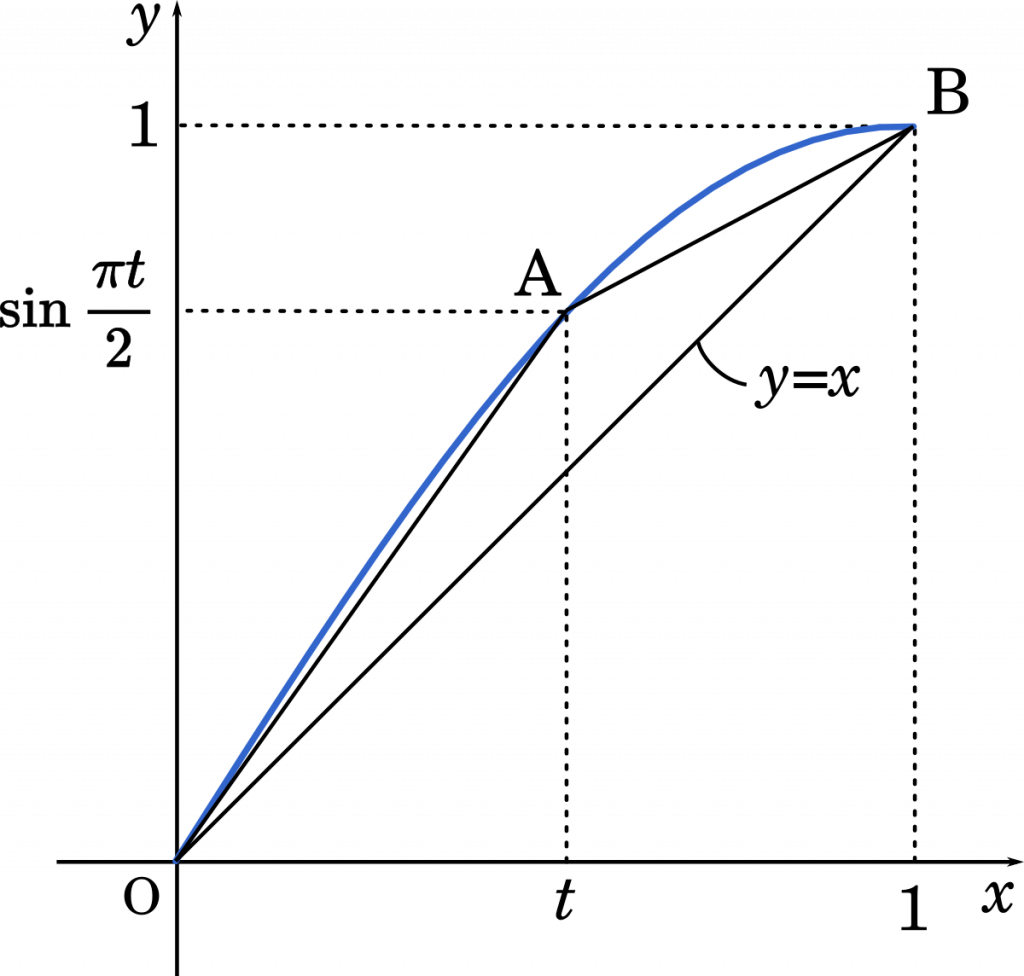
次に $x=t$ とおいて，グラフ上に点 A をつくります。そうすると，点 A は $y=x$ のグラフより上の方にあるので，$t<\sin\cfrac{\pi t}{2}$ の関係が成り立ちます。

したがって，$a_n<\sin\cfrac{\pi a_n}{2}=a_{n+1}$ となって，不等式が成り立つことがわかります。

証明したいのは不等式 $x<\sin\cfrac{\pi x}{2}$ ですが，この式を変形しても証明できそうにありません。

ここで，証明の一つのテクニックを習得しましょう。

直線 OA と直線 AB を比べると，(OAの傾き) > (ABの傾き) の関係になっていることがわかります。

このような状態であれば，点 A は 直線 $y=x$ の上側にあり，$x<f(x)$ が成り立つと言えるのです。

まず，(OAの傾き) > (ABの傾き) を証明していきます。

直線 OA の傾きは $\cfrac{\sin\cfrac{\pi t}{2}}{t}$
直線 AB の傾きは $\cfrac{1-\sin\cfrac{\pi t}{2}}{1-t}$

よって

$\cfrac{\sin\cfrac{\pi t}{2}}{t}>\cfrac{1-\sin\cfrac{\pi t}{2}}{1-t}$

これが成り立つことを示せばよい。

式を変形して

$\cfrac{\sin\cfrac{\pi t}{2}}{t}-\cfrac{1-\sin\cfrac{\pi t}{2}}{1-t}>0$

左辺を整理すると

$=\cfrac{(1-t)\sin\cfrac{\pi t}{2}-t\big(1-\sin\cfrac{\pi t}{2}\big)}{t(1-t)}$
$=\cfrac{\sin\cfrac{\pi t}{2}-t\sin\cfrac{\pi t}{2}-t+t\sin\cfrac{\pi t}{2}}{t(1-t)}$
$=\cfrac{\sin\cfrac{\pi t}{2}-t}{t(1-t)}$

$g(t)=\sin\cfrac{\pi t}{2}-t$ として
$g'(t)=\cfrac{\pi}{2}\cos\cfrac{\pi t}{2}-1$

$\cfrac{\pi}{2}\cos\cfrac{\pi t}{2}-1=0$ のとき
$\cos\cfrac{\pi t}{2}=\cfrac{2}{\pi}$

増減表は

$\def\arraystretch{1.5}\begin{array}{c||c|c|c|c|c|}t&(0)&\cdots&\frac{2}{\pi}&\cdots&(1)\\\hline g'(t)&(+)&+&0&-&(-)\\\hline g(t)&(0)&\nearrow&\text{最大}&\searrow&(0)\end{array}$

よって，$0<t<1$ のとき，$g(t)$ はつねに正の値をとるので

$\cfrac{\sin\cfrac{\pi t}{2}}{t}>\cfrac{1-\sin\cfrac{\pi t}{2}}{1-t}$

は成り立つ。

よって，$x<\sin\cfrac{\pi x}{2}$ である。

したがって，$x<\sin\cfrac{\pi x}{2}$ は

$x<f(x)$
$a_n<a_{n+1}$　（証明終わり）

グラフの形が分からないときは関数の増減を考える

(2)に進みます。

$b_n=\cfrac{1-a_{n+1}}{1-a_n}$
$=\cfrac{1-\sin\cfrac{\pi a_n}{2}}{1-a_n}$

証明したいのは $b_{n+1}<b_n$ だから，$\{b_n\}$ を一つの関数として考え，関数が単調減少であることを示すとよいでしょう。

$a_n=x$，$b_n=h(x)$ とおくと

$h(x)=\cfrac{1-\sin\cfrac{\pi x}{2}}{1-x}$

式を微分します。商の導関数の公式を思い出しましょう。

$h'(x)=\cfrac{\Big(1-\sin\cfrac{\pi x}{2}\Big)'(1-x)-\Big(1-\sin\cfrac{\pi x}{2}\Big)(1-x)’}{(1-x)^2}$
$=\cfrac{-\cfrac{\pi}{2}\cos\cfrac{\pi x}{2}(1-x)+1-\sin\cfrac{\pi x}{2}}{(1-x)^2}$
$=\cfrac{-\cfrac{\pi}{2}\cos\cfrac{\pi x}{2}+\cfrac{\pi x}{2}\cos\cfrac{\pi x}{2}+1-\sin\cfrac{\pi x}{2}}{(1-x)^2}$

$s(x)=-\cfrac{\pi}{2}\cos\cfrac{\pi x}{2}+\cfrac{\pi x}{2}\cos\cfrac{\pi x}{2}+1-\sin\cfrac{\pi x}{2}$ として

$s'(x)=\cfrac{\pi^2}{4}\sin\cfrac{\pi x}{2}+\Big(\cfrac{\pi x}{2}\Big)’\cos\cfrac{\pi x}{2}+\cfrac{\pi x}{2}\Big(\cos\cfrac{\pi x}{2}\Big)’-\cfrac{\pi}{2}\cos\cfrac{\pi x}{2}$
$=\cfrac{\pi^2}{4}\sin\cfrac{\pi x}{2}+\cfrac{\pi}{2}\cos\cfrac{\pi x}{2}-\cfrac{\pi^2 x}{4}\sin\cfrac{\pi x}{2}-\cfrac{\pi}{2}\cos\cfrac{\pi x}{2}$
$=\cfrac{\pi^2}{4}(1-x)\sin\cfrac{\pi x}{2}$

増減表は

$\def\arraystretch{1.5}\begin{array}{c||c|c|c|}x&(0)&\cdots&(1)\\\hline s'(x)&(+)&+&(+)\\\hline s(x)&1-\frac{\pi}{2}&\nearrow&0\end{array}$

$s(0)=-\cfrac{\pi}{2}\cos0+1=1-\cfrac{\pi}{2}$
$s(1)=-\cfrac{\pi}{2}\cos\cfrac{\pi}{2}+\cfrac{\pi}{2}\cos\cfrac{\pi}{2}+1-\sin\cfrac{\pi}{2}$
$=0$

よって，$h'(x)$ は $0<x<1$ においてつねに負の値となるので，$h(x)$ は $0<x<1$ において単調減少である。

したがって

$b_{n+1}<b_n$　（証明終わり）

はさみうちの原理・微分係数の定義

(3)に進みます。

とは言え，$a_n$ の式から極限に持ち込むことはできそうにないので，$b_n$ の式から考えてみましょう。

$b_n=\cfrac{1-a_{n+1}}{1-a_n}$
$0<a_n<1$ かつ $a_{n+1}>a_n$
$b_{n+1}<b_n$

式を変形して

$1-a_{n+1}=b_n(1-a_n)$

$1-a_n=c_n$ として
$c_{n+1}=b_n\cdot c_n$

$c_2=b_1\cdot c_1$
$c_3=b_2\cdot c_2$
$=b_2\cdot b_1\cdot c_1$
$c_4=b_3\cdot c_3$
$=b_3\cdot b_2\cdot b_1\cdot c_1$

つまり

$c_{n}=c_1\cdot b_1\cdot b_2\cdots b_{n-1}$

ここで，$b_{n+1}<b_n$ だから，$n\geqq2$ のとき，$b_{n}<b_1$ が成り立つ。

よって

$c_{n}=c_1\cdot b_1\cdot b_2\cdots b_{n-1}<c_1\cdot b_1\cdot b_1\cdots b_1 = c_1\cdot {b_1}^{n-1}$ ・・・①

また，$c_n=1-a_n$ であり，$0<a_n<1$ だから

$0<c_n<1$ ・・・②

①，②より

$0<c_n<c_1\cdot{b_1}^{n-1}$ ・・・③

$b_1$ を求めると

$b_1=\cfrac{1-a_2}{1-a_1}$
$=\cfrac{1-\sin\cfrac{\pi a_1}{2}}{1-a_1}$

(1)より $a_1<\sin\cfrac{\pi a_1}{2}$ だから，不等式を変形して

$1-a_1>1-\sin\cfrac{\pi a_1}{2}$

となるので

$b_1<1$

極限を求めると

$\displaystyle\lim_{n\rightarrow\infty}c_1\cdot{b_1}^{n-1}=0$

はさみうちの原理より

$\displaystyle\lim_{n\rightarrow\infty}c_n=0$
$\displaystyle\lim_{n\rightarrow\infty}(1-a_n)=0$

したがって

$\displaystyle\lim_{n\rightarrow\infty}a_n=1$　（答え）

次に，$b_n$ の極限を求めます。

$b_n=\cfrac{1-f(a_n)}{1-a_n}$

ここで，$f(a_n)=\sin\cfrac{\pi a_n}{2}=1$ となるとき，$a_n=1$ だから

$b_n=\cfrac{f(1)-f(a_n)}{1-a_n}$

と表すことができる。

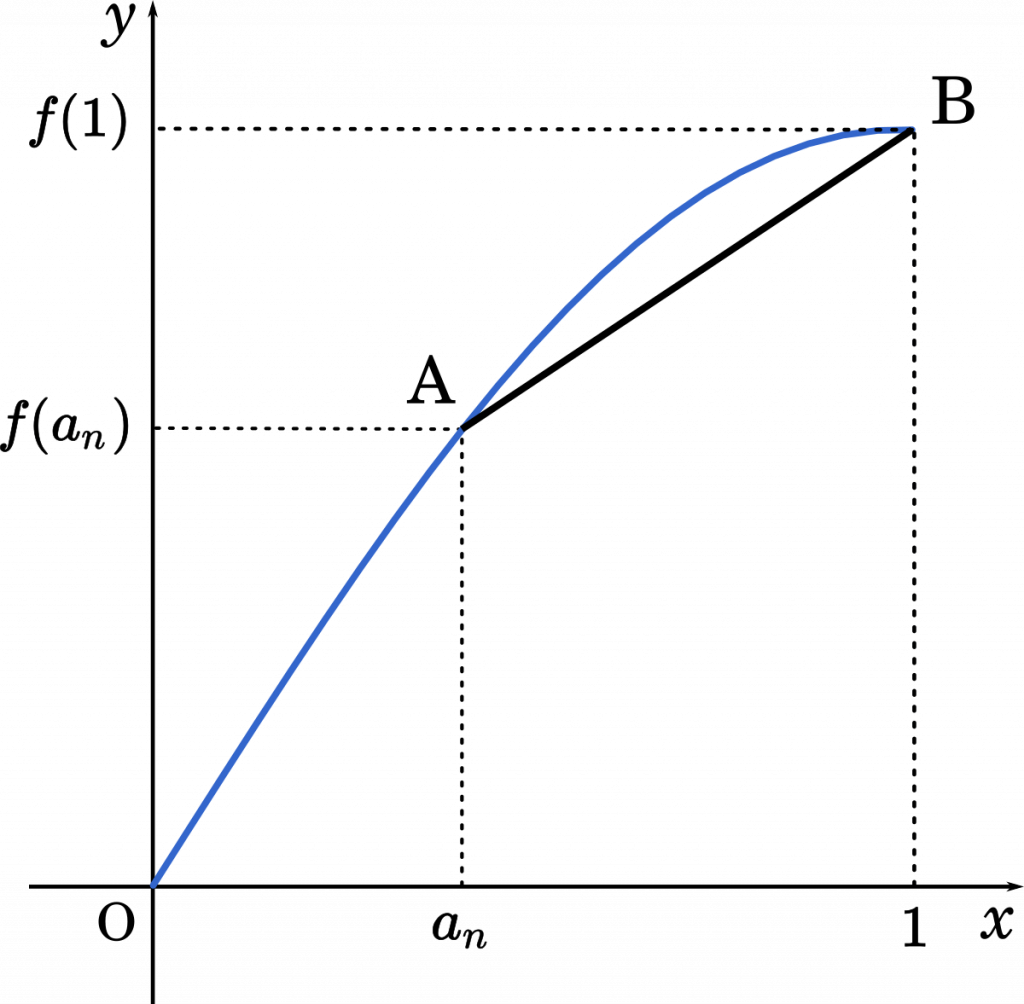
つまり，$b_n$ は直線 AB の傾きとなります。

極限を考えると

$\displaystyle\lim_{n\rightarrow\infty}\cfrac{f(1)-f(a_n)}{1-a_n}$
$\displaystyle=\lim_{n\rightarrow\infty}\cfrac{f(a_n)-f(1)}{a_n-1}$

$a_n=1+h$ とおくと，$n\rightarrow\infty$ のとき $1=1+h$ つまり，$h=0$ となるから

$\displaystyle=\lim_{h\rightarrow0}\cfrac{f(1+h)-f(1)}{1+h-1}$
$\displaystyle=\lim_{h\rightarrow0}\cfrac{f(1+h)-f(1)}{h}$

$=f'(1)$
$=\cos\cfrac{\pi}{2}=0$

したがって

$\displaystyle\lim_{n\rightarrow\infty}b_n=0$　（答え）