【数III積分】曲線の長さを求める公式の仕組み（媒介変数を用いる場合と用いない場合）

曲線の長さを積分を用いて求めます。

媒介変数表示を用いる場合

直線の例で考える

簡単な例で具体的に見てみましょう。

例えば，次の式で表される線の長さを求めます。

$\begin{cases}x=2t\\y=3t\end{cases}$

$t=1$ なら，$(x,y)=(2,3)$ で，$t=2$ なら $(x,y)=(4,6)$ です。

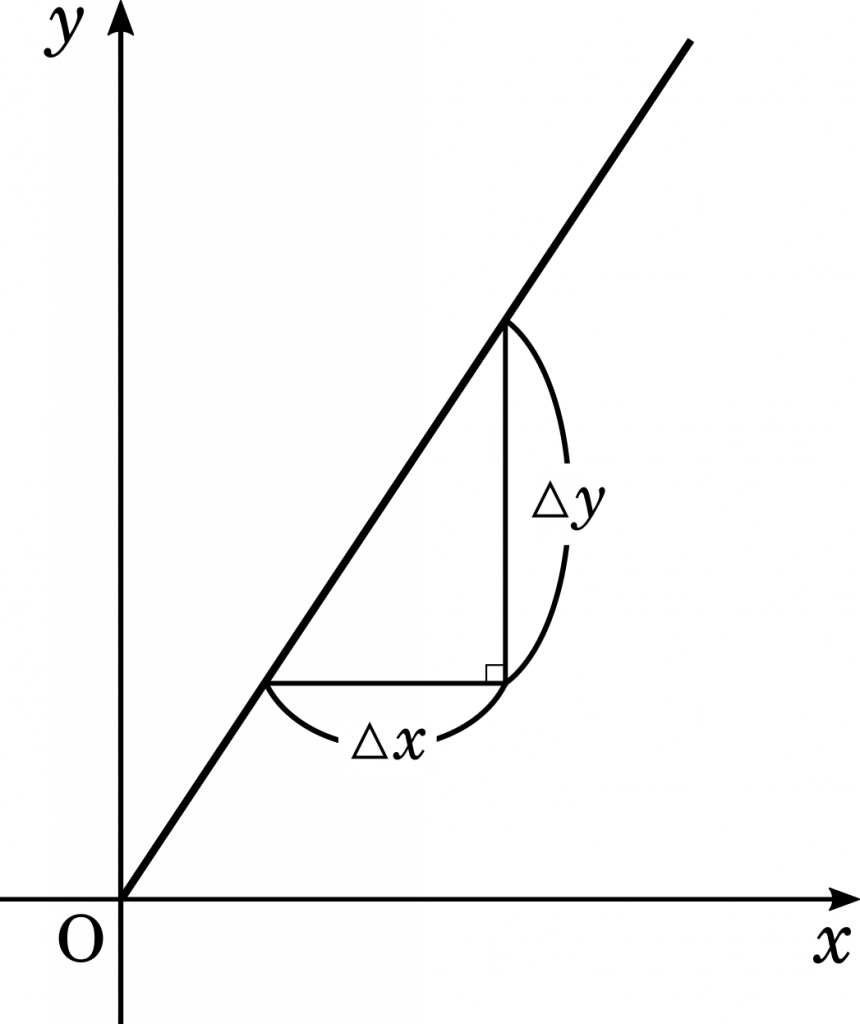
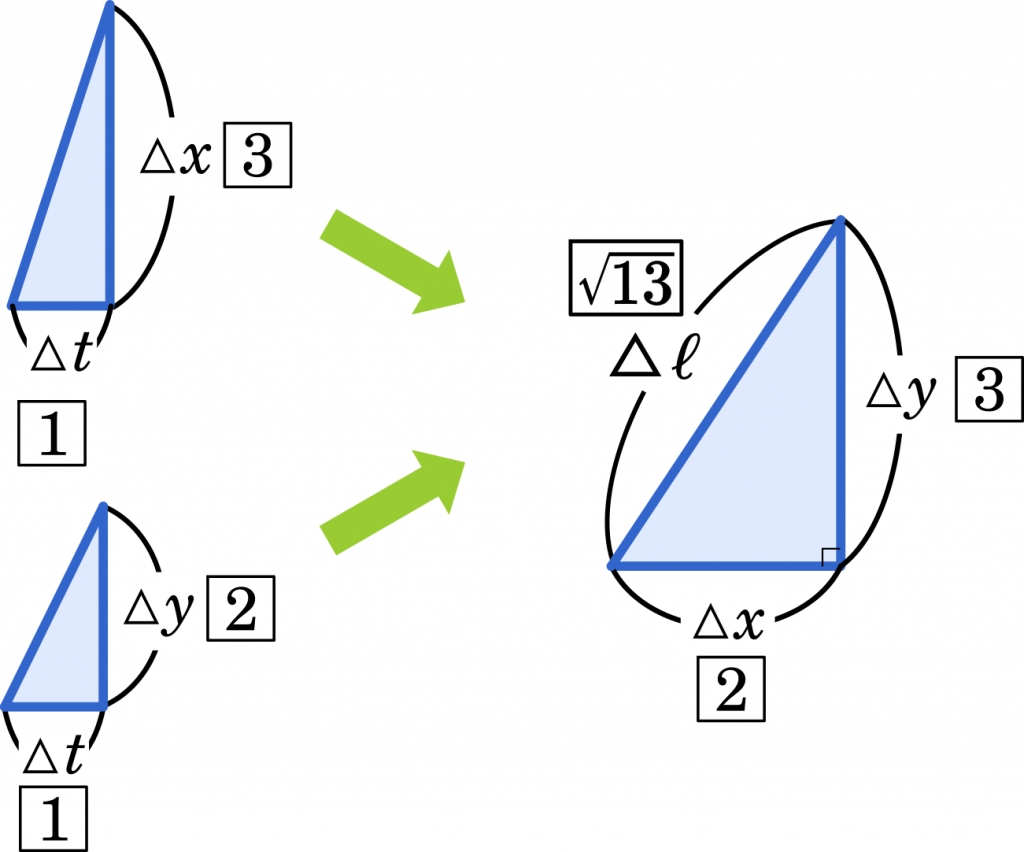
このとき，グラフの $\Delta x,\Delta y$ は $t$ の変位によって決まります。$\Delta t=1$ ならば，$\Delta x=2,\Delta y=3$ となります。
そして出来上がった三角形の斜辺の長さを三平方の定理を用いて求めると

$\Delta\ell=\sqrt{(\Delta x)^2+(\Delta y)^2}$
$=\sqrt{2^2+3^2}=\sqrt{13}$

つまり，$t$ の大きさが $1$ 変化すると直線の長さは $\sqrt{13}$ ずつ変化していくことが分かります。

$\displaystyle L=\int \sqrt{\Big(\cfrac{dx}{dt}\Big)^2+\Big(\cfrac{dy}{dt}\Big)^2}\space dt$
$\displaystyle =\int \sqrt{2^2+3^2}\space dt=\sqrt{13}t$ （積分定数は省略）

直線の長さが $t$ と比例の関係になりました。この積分は，$t$ の変位である $\Delta t$ を限りなく細かくして，そこから求められる斜辺の長さを積み上げています。直線の場合，その結果は単に $t$ に比例します。

曲線の長さを求める

同じ手順で，曲線の長さを求めてみます。

先ほどと違い，曲線の場合は，$\Delta t$ と $\Delta x,\Delta y$ の比は一定ではなく $t$ の値によって変化します。それでも，考え方は先ほどと同じです。

実際に，例題を解きながらイメージをつかんでみます。

[問題]　曲線の長さを求めよ。

$\begin{cases}x=\sin t-t\cos t\\y=\cos t+t\sin t\end{cases}$ ($0$ ≦ $t$ ≦ $1$)

$\cfrac{dx}{dt}=\cos t-\{t’\cos t+t(\cos t)’\}$
$=\cos t-(\cos t-t\sin t)$
$=\cos t-\cos t+t\sin t$
$=t\sin t$

$y$ についても同様に
$\cfrac{dy}{dt}=-\sin t+\{t’\sin t+t(\sin t)’\}$
$=-\sin t+(\sin t+t\cos t)$
$=t\cos t$

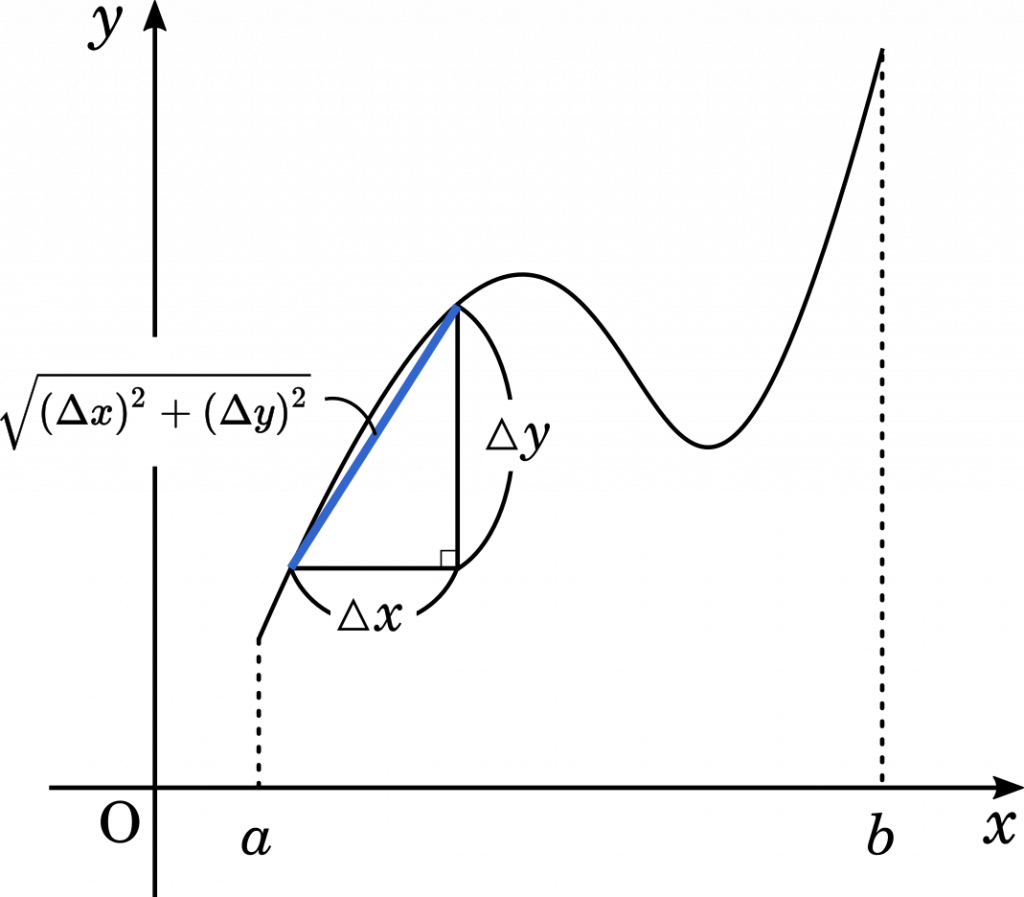
$t$ の値が変化したとして，その変位を $\Delta t$ とするなら，それをもとに $x,y$ は $\Delta x,\Delta y$ だけ変化します。

したがって，曲線の長さは

$\displaystyle L=\int_0^1 \sqrt{(\Delta x)^2+(\Delta y)^2}\space dt$
$\displaystyle =\int_0^1 \sqrt{(t\sin t)^2+(t\cos t)^2}\space dt$
$\displaystyle =\int_0^1 t\sqrt{\sin^2t+\cos^2 t}\space dt$
$\displaystyle =\int_0^1 t\space dt$
$=\Big[\cfrac{t^2}{2}\Big]_0^1$
$=\cfrac{1}{2}$　（答え）

積分によって，$\Delta x,\Delta y$ を限りなく細かくしていくと，ごく小さな三角形ができあがり，三平方の定理でその斜辺の長さを求めてひたすら積み上げていく，というイメージです。

曲線の長さのもう一つの表し方

曲線の長さの求め方にはもう一つ，媒介変数を用いないパターンもあります。

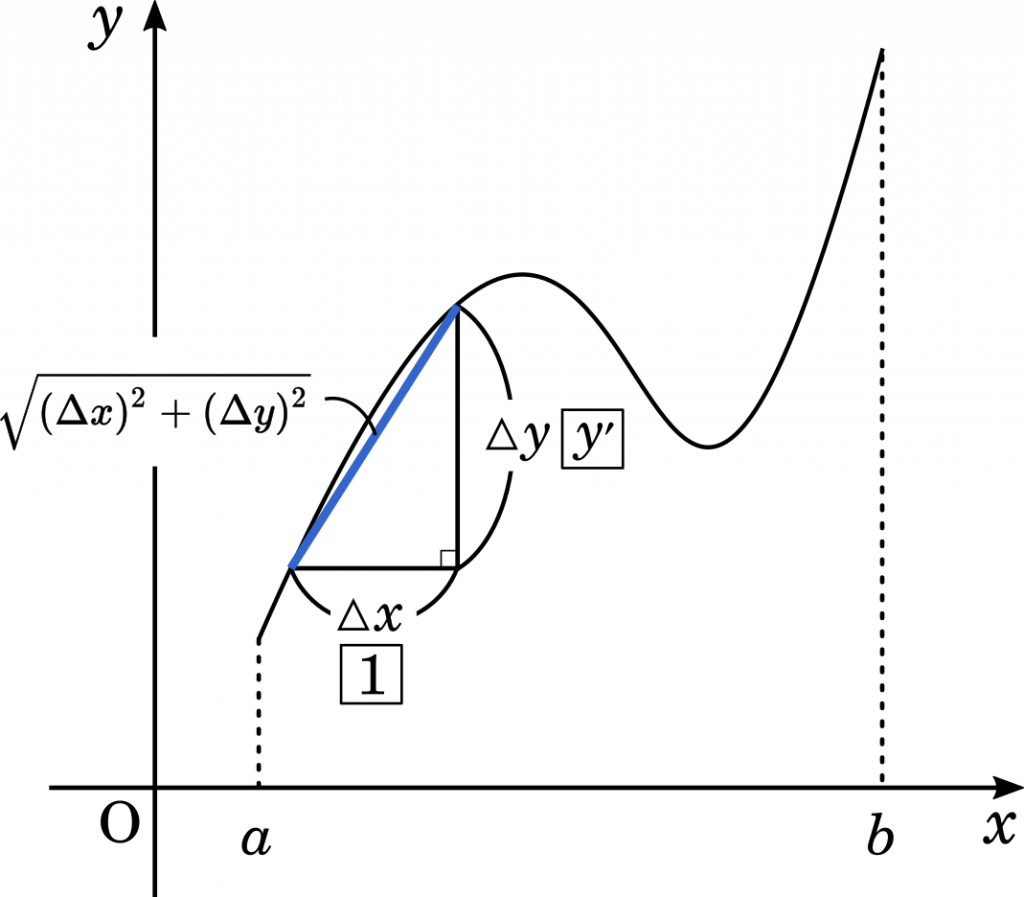
$y’$ は接線の傾きのことですが，たとえば $y’=2$ というのは $x$ の変化量が $1$ に対して $y$ の変化量が $2$ であるという意味です。普段意識することはありませんが，微分して $y’$ を求めるとき，実際には $x$ の変化量を $1$ に見立て，それに対する比として $y’$ を表しています。

[問題]曲線の長さを求めよ。

$y=\cfrac{3}{2}(e^{\small{\frac{x}{3}}}+e^{\small{-\frac{x}{3}}})$　($-6$ ≦ $x$ ≦ $6$)

式を $x$ で微分すると

$y’=\cfrac{3}{2}\Big\{e^{\small{\frac{x}{3}}}\cdot\cfrac{1}{3}+e^{\small{-\frac{x}{3}}}\cdot\Big(-\cfrac{1}{3}\Big)\Big\}$
$=\cfrac{1}{2}(e^{\small{\frac{x}{3}}}-e^{\small{-\frac{x}{3}}})$

よって，曲線の長さは

$\displaystyle L=\int_{-6}^6\sqrt{1+\Big\{\cfrac{1}{2}(e^{\small{\frac{x}{3}}}-e^{\small{-\frac{x}{3}}})\Big\}^2}\space dx$

ここで

$\sqrt{1+\Big\{\cfrac{1}{2}(e^{\small{\frac{x}{3}}}-e^{\small{-\frac{x}{3}}})\Big\}^2}$
$=\sqrt{1+\cfrac{1}{4}(e^{\small{\frac{2}{3}x}}-2e^{\small{\frac{x}{3}}}e^{\small{-\frac{x}{3}}}+e^{\small{-\frac{2}{3}x}})}$

$e^{\small{\frac{x}{3}}}e^{\small{-\frac{x}{3}}}=e^{\small{\frac{x}{3}-\frac{x}{3}}}=e^0=1$ に注意して

$=\sqrt{1+\cfrac{1}{4}(e^{\small{\frac{2}{3}x}}-2+e^{\small{-\frac{2}{3}x}})}$
$=\sqrt{1+\cfrac{1}{4}(e^{\small{\frac{2}{3}x}}-2+e^{\small{-\frac{2}{3}x}})}$
$=\sqrt{1+\cfrac{1}{4}e^{\small{\frac{2}{3}x}}-\cfrac{1}{2}+\cfrac{1}{4}e^{\small{-\frac{2}{3}x}}}$
$=\sqrt{1+\cfrac{1}{4}e^{\small{\frac{2}{3}x}}-\cfrac{1}{2}+\cfrac{1}{4}e^{\small{-\frac{2}{3}x}}}$
$=\sqrt{\cfrac{1}{4}e^{\small{\frac{2}{3}x}}+\cfrac{1}{2}+\cfrac{1}{4}e^{\small{-\frac{2}{3}x}}}$
$=\sqrt{\cfrac{1}{4}(e^{\small{\frac{2}{3}x}}+2+e^{\small{-\frac{2}{3}x}})}$

先ほどの $1=e^{\small{\frac{x}{3}}}e^{\small{-\frac{x}{3}}}$ を利用して

$=\sqrt{\cfrac{1}{4}(e^{\small{\frac{2}{3}x}}+2e^{\small{\frac{x}{3}}}e^{\small{-\frac{x}{3}}}+e^{\small{-\frac{2}{3}x}})}$
$=\sqrt{\cfrac{1}{4}(e^{\small{\frac{x}{3}}}+e^{\small{-\frac{x}{3}}})^2}$
$=\cfrac{1}{2}(e^{\small{\frac{x}{3}}}+e^{\small{-\frac{x}{3}}})$

したがって

$\displaystyle L=\int_{-6}^6 \cfrac{1}{2}(e^{\small{\frac{x}{3}}}+e^{\small{-\frac{x}{3}}})\space dx$
$=\cfrac{1}{2}\Big[e^{\small{\frac{x}{3}}}\cdot3+e^{\small{-\frac{x}{3}}}(-3)\Big]_{-6}^6$
$=\cfrac{3}{2}\Big[e^{\small{\frac{x}{3}}}-e^{\small{-\frac{x}{3}}}\Big]_{-6}^6$
$=\cfrac{3}{2}\Big\{e^{\small{\frac{6}{3}}}-e^{\small{-\frac{6}{3}}}-\Big(e^{\small{-\frac{6}{3}}}-e^{\small{\frac{6}{3}}}\Big)\Big\}$
$=\cfrac{3}{2}(2e^2-2e^{-2})$
$=3(e^2-e^{-2})$
$=3\Big(e^2-\cfrac{1}{e^2}\Big)$　（答え）