【数III積分】区分求積法の考え方と使い方を整理する

区分求積法の公式は以下のようになります。

$\displaystyle\lim_{n\rightarrow\infty}\cfrac{\space1\space}{n}\sum_{k=1}^n f\Big(\cfrac{\space k\space}{n}\Big)=\int_0^1 f(x)\space dx$

区分求積法とは，求めたい部分の面積を小さな長方形に分割していく方法です。

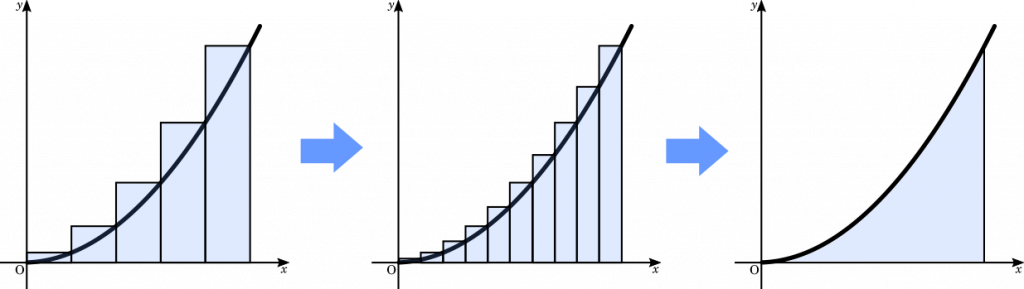
長方形の面積を考える

$f(x)=x^2$ を使って考えてみましょう。まずは試しに 5 分割してみます。

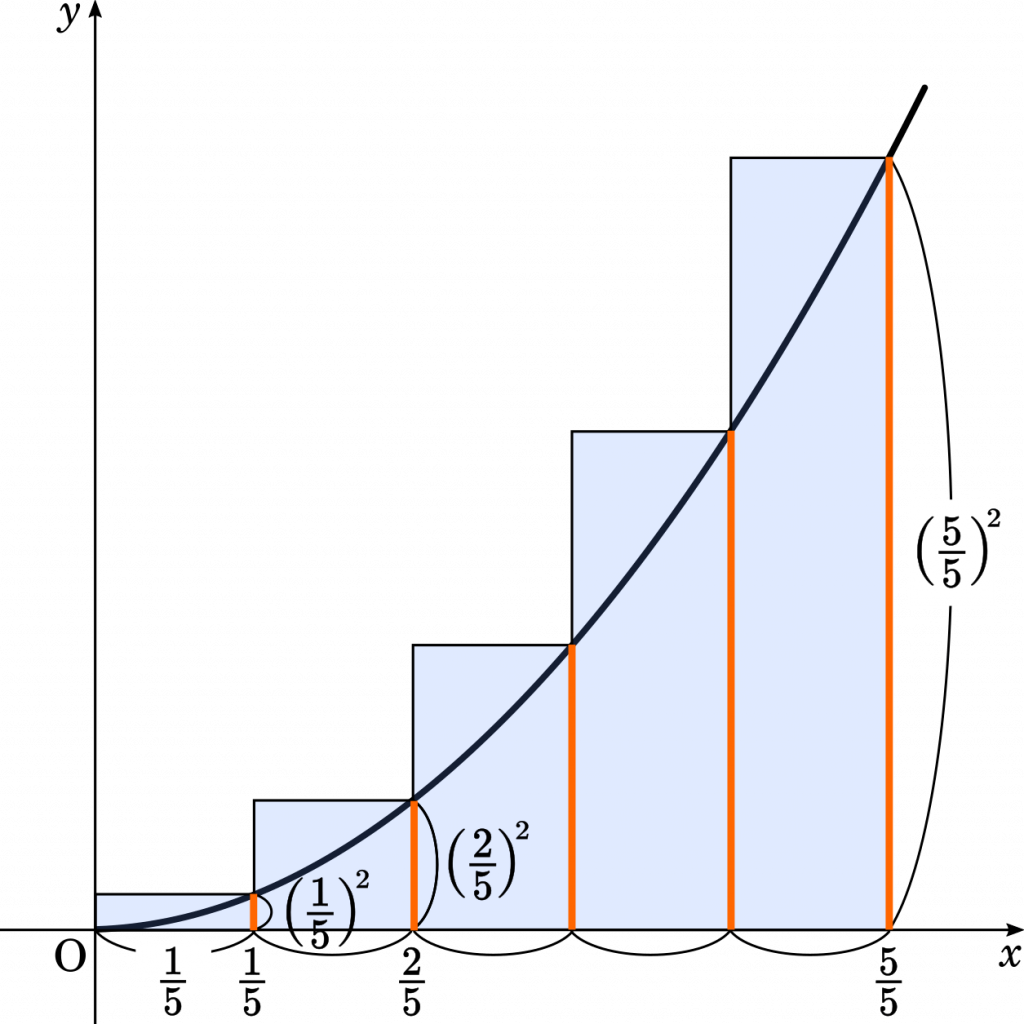
一番左の長方形の面積を考えると，底辺が $\cfrac{1}{5}$，高さが $\Big(\cfrac{1}{5}\Big)^2$ です。

2 番目の長方形は，底辺 $\cfrac{1}{5}$，高さ $\Big(\cfrac{2}{5}\Big)^2$ です。

これらを足し合わせたものが全体の面積だから

$S=\cfrac{1}{5}\times\cfrac{1}{5}+\cfrac{1}{5}\times\Big(\cfrac{2}{5}\Big)^2+\cfrac{1}{5}\times\Big(\cfrac{3}{5}\Big)^2+\cfrac{1}{5}\times\Big(\cfrac{4}{5}\Big)^2+\cfrac{1}{5}\times\Big(\cfrac{5}{5}\Big)^2$
$=\cfrac{1}{5}\Big\{\cfrac{1}{5}+\Big(\cfrac{2}{5}\Big)^2+\Big(\cfrac{3}{5}\Big)^2+\Big(\cfrac{4}{5}\Big)^2+\Big(\cfrac{5}{5}\Big)^2\Big\}$
$\displaystyle=\cfrac{1}{5}\sum_{k=1}^5\Big(\cfrac{k}{5}\Big)^2$

今度は 5 分割ではなく $n$ 分割してみます。

よって，面積は

$\displaystyle S=\cfrac{1}{n}\sum_{k=1}^n\Big(\cfrac{k}{n}\Big)^2$

式を計算すると

$\displaystyle S=\cfrac{1}{n}\cdot\cfrac{1}{n^2}\sum_{k=1}^n k^2$
$=\cfrac{1}{n^3}\cdot\cfrac{1}{6}n(n+1)(2n+1)$
$=\cfrac{1}{6n^2}(2n^2+n+2n+1)$
$=\cfrac{1}{6n^2}(2n^2+3n+1)$
$=\cfrac{1}{3}+\cfrac{1}{2n}+\cfrac{1}{6n^2}$

$\displaystyle\lim_{n\rightarrow\infty}\cfrac{1}{3}+\cfrac{1}{2n}+\cfrac{1}{6n^2}=\cfrac{1}{3}$

ちなみに，積分で求めると

$\displaystyle\int_0^1 x^2\space dx=\Big[\cfrac{x^3}{3}\Big]_0^1=\cfrac{1}{3}$

これで答えが正しいことが分かります。

もう一つの方法で長方形の面積を求める

次に，長方形の左側を高さとして考えるパターンをやります。

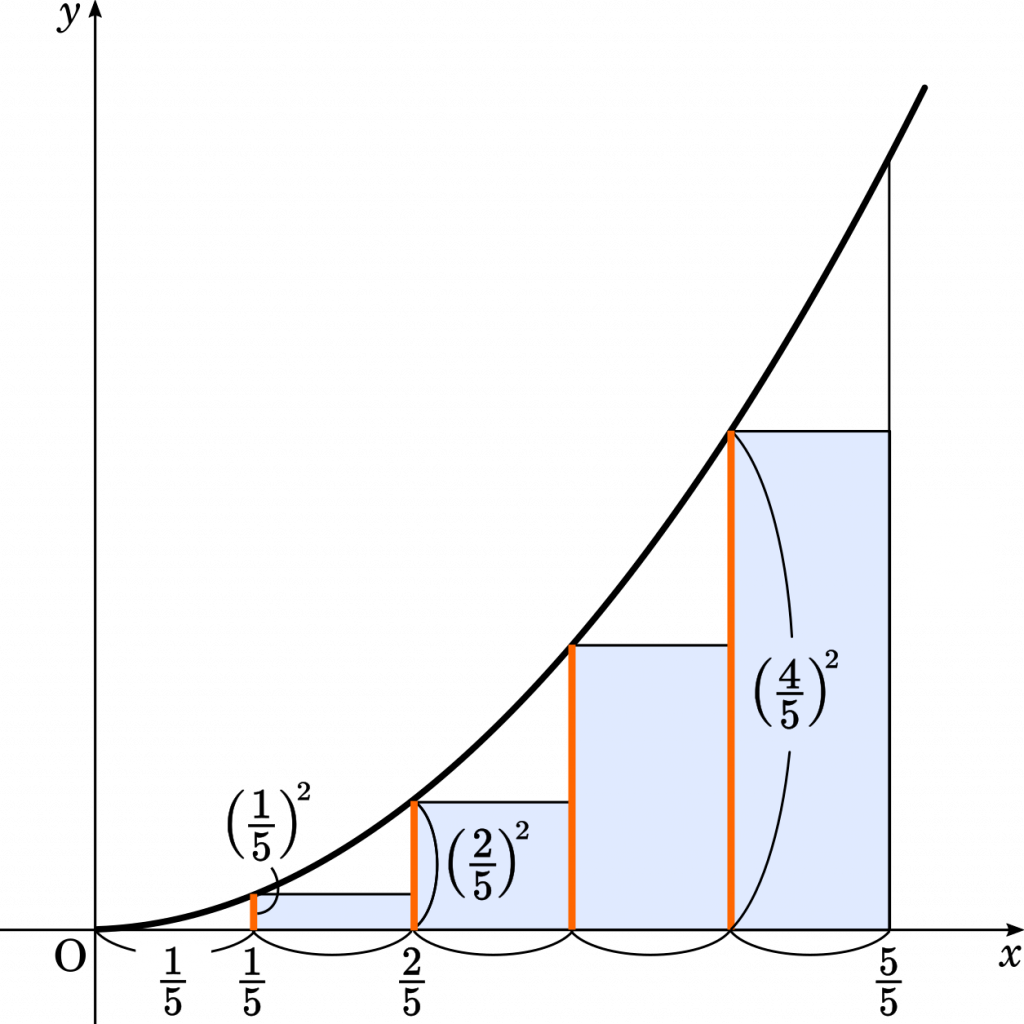
まず，一番左の長方形は，底辺の長さ $\cfrac{1}{5}$，高さ $0$ とみなすことができます。したがって，グラフ上には描かれません。

左から２番目は，底辺 $\cfrac{1}{5}$，高さ $\Big(\cfrac{2}{5}\Big)^2$ です。

面積を合計すると

$S=\cfrac{1}{5}\times0+\cfrac{1}{5}\times\Big(\cfrac{2}{5}\Big)^2+\cfrac{1}{5}\times\Big(\cfrac{3}{5}\Big)^2+\cfrac{1}{5}\times\Big(\cfrac{4}{5}\Big)^2$
$=\cfrac{1}{5}\Big\{0+\Big(\cfrac{2}{5}\Big)^2+\Big(\cfrac{3}{5}\Big)^2+\Big(\cfrac{4}{5}\Big)^2\Big\}$
$\displaystyle=\cfrac{1}{5}\sum_{k=0}^4\Big(\cfrac{k}{5}\Big)^2$

となります。

これが 5 分割ではなく，$n$ 分割だとすると

$\displaystyle S=\cfrac{1}{n}\sum_{k=0}^{n-1}\Big(\cfrac{k}{n}\Big)^2$

さきほどは，$\displaystyle\sum_{k=1}^n$ だったのが，$\displaystyle\sum_{k=0}^{n-1}$ になっているところに注意しましょう。

これを計算すると

$=\displaystyle\cfrac{1}{n}\cdot\cfrac{1}{n^2}\sum_{k=0}^{n-1}k^2$

$k=0$ のとき，$k^2=0$ です。

$\displaystyle\sum_{k=0}^{n-1}k^2=0^2+1^2+2^2+\cdots+(n-1)^2$
$\displaystyle\sum_{k=1}^{n-1}k^2=1^2+2^2+\cdots+(n-1)^2$

だから

$\displaystyle\sum_{k=0}^{n-1} k^2=\sum_{k=1}^{n-1} k^2$

よって

$\displaystyle S=\cfrac{1}{n^3}\sum_{k=1}^{n-1}k^2$

$=\cfrac{1}{n^3}\cdot\cfrac{1}{6}(n-1)(n-1+1)\{2(n-1)+1\}$
$=\cfrac{1}{6n^3}(n-1)n(2n-2+1)$
$=\cfrac{1}{6n^2}(n-1)(2n-1)$
$=\cfrac{1}{6n^2}(2n^2+n-2n+1)$
$=\cfrac{1}{6n^2}(2n^2-n+1)$
$=\cfrac{1}{3}-\cfrac{1}{6n}+\cfrac{1}{6n^2}$

これを $n\rightarrow\infty$ とすると

$S=\cfrac{1}{3}$

さきほどと同じ結果になりました。

はさみうちの原理との関係

こうして二通りの方法で面積を求めたのですが，これらを並べてみると次のような関係があります。

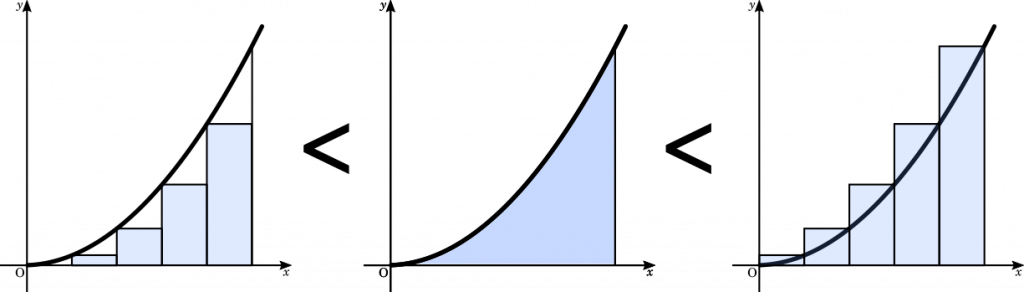
これを不等式にすると

$\displaystyle\lim_{n\rightarrow\infty}\cfrac{1}{n^3}\sum_{k=1}^{n}k^2<\int_0^1 f(x)\space dx<\lim_{n\rightarrow\infty}\cfrac{1}{n^3}\sum_{k=0}^{n-1}k^2$
$\displaystyle\cfrac{1}{3}<\int_0^1 f(x)\space dx<\cfrac{1}{3}$

はさみうちの原理より

$\displaystyle\int_0^1 f(x)\space dx=\cfrac{1}{3}$

このようにはさみうちの原理を用いて積分の答えを導くことができます。

今回は例題なので，普通に積分すれば済むのですが，式が複雑になってそのまま積分をすることが難しいときに，この考え方でうまくいくことがあります。

公式を導く

ここまでやってきたことを公式にしてみましょう。まず，区間は $[0,1]$ とします。これを $n$ 分割すると，長方形の底辺は $\cfrac{1}{n}$ です。

また，$x$ の値は $\cfrac{1}{n},\cfrac{2}{n},\cfrac{3}{n},\cdots,\cfrac{n}{n}$ と変化していきます。そのとき，長方形の高さ $y=f(x)$ は，$f\Big(\cfrac{1}{n}\Big),f\Big(\cfrac{2}{n}\Big),f\Big(\cfrac{3}{n}\Big),\cdots,f\Big(\cfrac{n}{n}\Big)$ と表すことができます。

長方形の面積の合計は

$S=\cfrac{1}{n}\cdot f\Big(\cfrac{1}{n}\Big)+\cfrac{1}{n}\cdot f\Big(\cfrac{2}{n}\Big)+\cfrac{1}{n}\cdot f\Big(\cfrac{3}{n}\Big)+\cdots+\cfrac{1}{n}\cdot f\Big(\cfrac{n}{n}\Big)$
$=\cfrac{1}{n}\Big\{f\Big(\cfrac{1}{n}\Big)+f\Big(\cfrac{2}{n}\Big)+f\Big(\cfrac{3}{n}\Big)+\cdots+f\Big(\cfrac{n}{n}\Big)\Big\}$
$\displaystyle=\cfrac{\space1\space}{n}\sum_{k=1}^n f\Big(\cfrac{\space k\space}{n}\Big)$

$n$ 分割を限りなく細かくしていくと

$\displaystyle\lim_{n\rightarrow\infty}\cfrac{\space1\space}{n}\sum_{k=1}^n f\Big(\cfrac{\space k\space}{n}\Big)=\int_0^1 f(x)\space dx$

例題にチャレンジ

次の極限値を求めよ。 $\displaystyle\lim_{n\rightarrow\infty}\sum_{k=1}^n\cfrac{n}{k^2+n^2}$

$\displaystyle\lim_{n\rightarrow\infty}\sum_{k=1}^n\cfrac{n}{k^2+n^2}$

分子，分母をそれぞれ $n^2$ で割ると

$\displaystyle\lim_{n\rightarrow\infty}\sum_{k=1}^n\cfrac{n}{k^2+n^2}$
$\displaystyle=\lim_{n\rightarrow\infty}\sum_{k=1}^n\cfrac{\cfrac{n}{n^2}}{\cfrac{k^2}{n^2}+\cfrac{n^2}{n^2}}$
$\displaystyle=\lim_{n\rightarrow\infty}\sum_{k=1}^n\cfrac{\cfrac{1}{n}}{\Big(\cfrac{k}{n}\Big)^2+1}$
$\displaystyle=\lim_{n\rightarrow\infty}\sum_{k=1}^n\cfrac{1}{n}\times\cfrac{1}{\Big(\cfrac{k}{n}\Big)^2+1}$
$\displaystyle=\lim_{n\rightarrow\infty}\cfrac{1}{n}\sum_{k=1}^n\cfrac{1}{\Big(\cfrac{k}{n}\Big)^2+1}$

もう一度公式を確認すると

$\displaystyle\lim_{n\rightarrow\infty}\cfrac{\space1\space}{n}\sum_{k=1}^n f\Big(\cfrac{\space k\space}{n}\Big)=\int_0^1 f(x)\space dx$

つまり，$\cfrac{k}{n}$ を $x$ にすれば良いということです。したがって

$\displaystyle=\int_0^1 \cfrac{1}{x^2+1}\space dx$

あとはこの積分を解いていきます。

$x=\tan\theta$ とおくと

$dx=\cfrac{1}{\cos^2\theta}\space d\theta$

また

$\def\arraystretch{1.5}\begin{array}{c|c}x & 0\rightarrow 1\\\hline \theta & 0\rightarrow\frac{\pi}{4}\end{array}$

よって，与式は

$\displaystyle=\int_0^{\small{\frac{4}{\pi}}} \cfrac{1}{1+\tan^2\theta}\cdot\cfrac{1}{\cos^2\theta}d\theta$
$\displaystyle=\int_0^{\small{\frac{4}{\pi}}} \cfrac{1}{\cfrac{1}{\cos^2\theta}}\cdot\cfrac{1}{\cos^2\theta}d\theta$
$\displaystyle=\int_0^{\small{\frac{4}{\pi}}} 1\space d\theta$
$=\Big[\theta\Big]_0^{\small{\frac{\pi}{4}}}=\cfrac{\pi}{4}$　（答え）