【数III】関数の連続と微分可能ってどういうこと?を図解してみる


微分可能と連続
まず,定義を確認します。
関数 $f(x)$ が $x=a$ で微分可能ならば,$x=a$ で連続である。
例として,$f(x)=x^2$ で考えてみます。これが,$x=1$ で微分可能かどうかを調べてみます。


微分可能な場合
微分係数
$\displaystyle f'(a)=\lim_{h\rightarrow0}\cfrac{f(a+h)-f(a)}{h}=\lim_{x\rightarrow a}\cfrac{f(x)-f(a)}{x-a}$
ここで,右側微分と左側微分を行います。
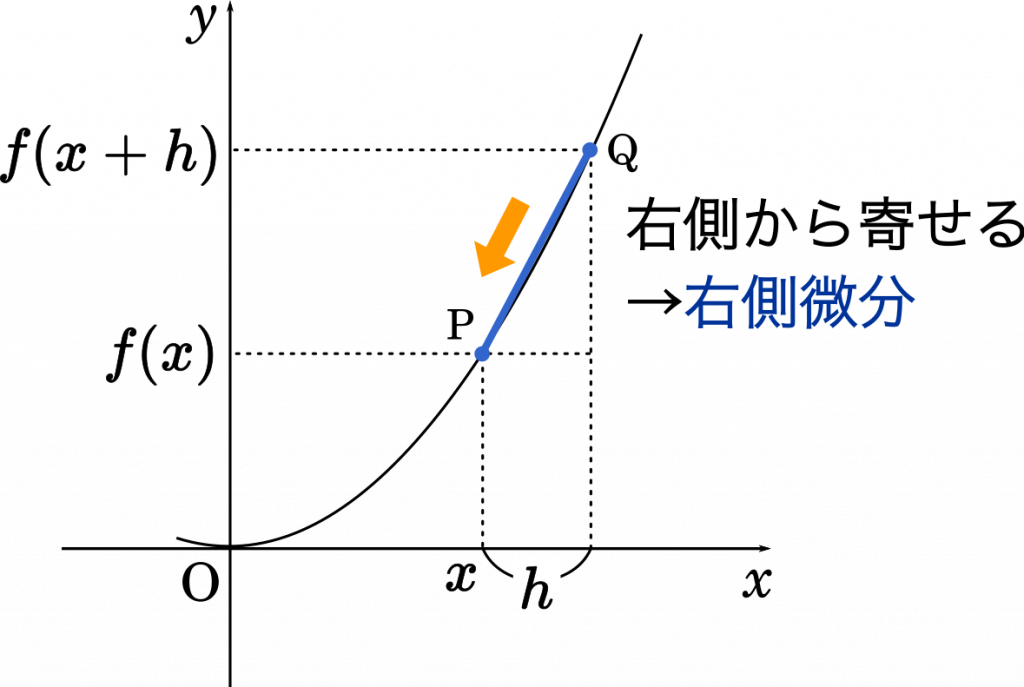

このように $h$ を $x$ の右側にとることを右側微分と言います。極限の計算では,$h\rightarrow+0$ と表します。
$f(x)=x^2,x=1$ とすると
$\displaystyle\lim_{h\rightarrow+0}\cfrac{(1+h)^2-1^2}{h}$
$\displaystyle\lim_{h\rightarrow+0}\cfrac{1+2h+h^2-1}{h}$
$\displaystyle\lim_{h\rightarrow+0}\cfrac{2h+h^2}{h}$
$\displaystyle\lim_{h\rightarrow+0}(2+h)$
$=2$

今度は $h$ を $x$ の左側にとります。これを左側微分と言い,極限の計算では,$h\rightarrow-0$ と表します。
$\displaystyle\lim_{h\rightarrow-0}\cfrac{(1+h)^2-1^2}{h}$
$\displaystyle\lim_{h\rightarrow-0}\cfrac{1+2h+h^2-1}{h}$
$\displaystyle\lim_{h\rightarrow-0}\cfrac{2h+h^2}{h}$
$\displaystyle\lim_{h\rightarrow-0}(2+h)$
$=2$


こうして,右側微分と左側微分の値が一致しました。このとき関数は $x=1$ で微分可能である,と言います。
右側微分と左側微分が一致 ⇒ 微分可能
微分可能かどうかの判定は,このように右側微分と左側微分を計算することで行います。
微分可能ではない場合
次に,関数 $f(x)=|2x(x-1)|$ において $x=0$ で微分可能かどうかを調べてみましょう。
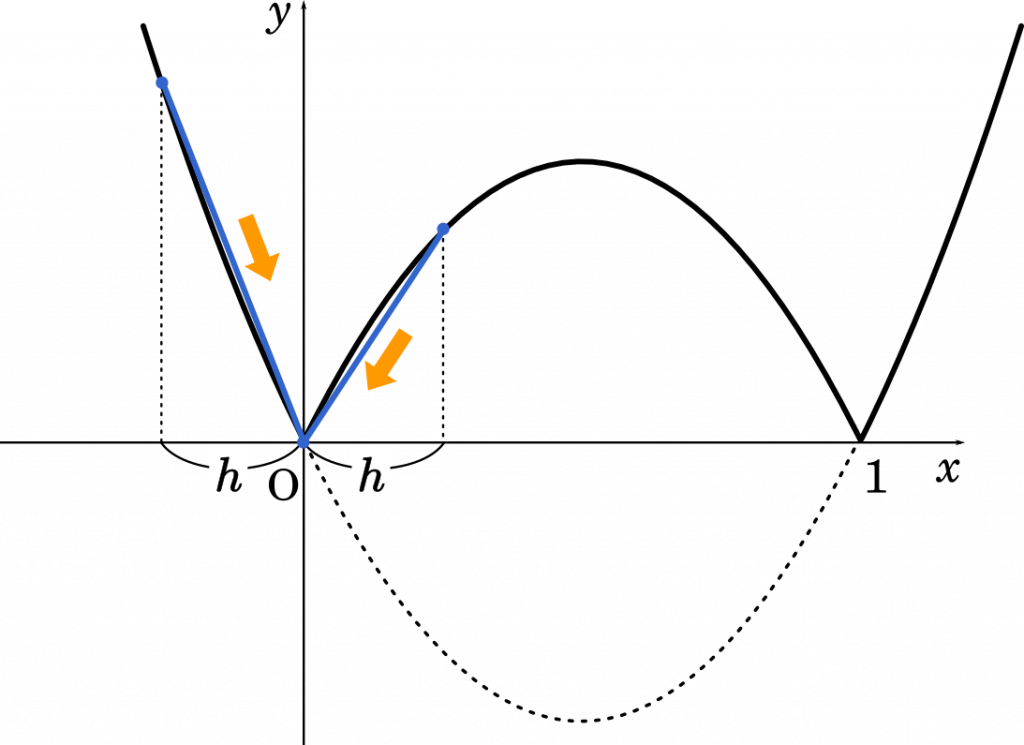
グラフで表すと上のようになります。$x=0$ のところを見てみると,グラフが角のように折れ曲がっていることが分かります。
先ほどと同じように左右から微分してみましょう。

右側微分から考えていきます。$0$ ≦ $x$ ≦ $1$ の区間では絶対値の中の式 $2x(x-1)$ はマイナスになります。そのため,右側から極限を求めるときには式の符号を逆にする必要があります。

$\displaystyle\lim_{h\rightarrow+0}\cfrac{f(0+h)-f(0)}{h}$
$\displaystyle=\lim_{h\rightarrow+0}\cfrac{-\{2(0+h)(0+h-1)\}-0}{h}$

$\displaystyle=\lim_{h\rightarrow+0}\cfrac{-2h(h-1)}{h}$
$\displaystyle=\lim_{h\rightarrow+0}-2(h-1)$
$=2$
次に左側微分です。
$\displaystyle\lim_{h\rightarrow-0}\cfrac{f(0+h)-f(0)}{h}$



$\displaystyle=\lim_{h\rightarrow-0}\cfrac{2(0+h)(0+h-1)-0}{h}$
$\displaystyle=\lim_{h\rightarrow-0}\cfrac{2h(h-1)}{h}$
$\displaystyle=\lim_{h\rightarrow-0}2(h-1)$
$=-2$
左右で微分係数が一致しませんでした。つまり,式は $x=0$ で微分可能ではない,というのが答えです。


SNSでシェア