【数III】2 つの放物線に接する3本の直線を求める(千葉大2020第7問)

方針として，まず放物線の接線の式をつくり，その直線がもう一つの放物線と接する条件を考えます。そして，それに当てはまる点が放物線上に 3 か所できる $a$ の条件を求めればできあがりです。

まず，$x=\cfrac{1}{2a}y^2+\cfrac{3a}{4}$ から接線の式をつくっていきます。

接線の傾きを求めるために $x=\cfrac{1}{2a}y^2+\cfrac{3a}{4}$ を $x$ で微分します。

$y=x^2$ ・・・①
$x=\cfrac{1}{2a}y^2+\cfrac{3a}{4}$ ・・・②

①を $x$ で微分すると

$y’=2x$ ・・・③

②を $x$ で微分すると

$1=\cfrac{1}{2a}\cdot2yy’$
$y’=\cfrac{a}{y}$ ・・・④

ここで，②の放物線上の点を$(X,Y)$とすると

$X=\cfrac{1}{2a}Y^2+\cfrac{3a}{4}$　・・・⑤
$Y’=\cfrac{a}{Y}$　・・・⑥

通常なら，こういったタイプの問題は $x$ 座標を $t$ とおいて考えていきます。しかし，今回は放物線の式が $y=$ ～ ではなく，$x=$ ～ の形になっているので $y$ 座標のほうを $Y$ とおいて考えていくとうまくいきます。

よって，⑤，⑥より接線の式は

$y=Y'(x-X)+Y$

これが $y=x^2$ と接するので

$Y'(x-X)+Y=x^2$
$x^2-Y'(x-X)-Y=0$
$x^2-Y’x+XY’-Y=0$

$D=Y’^2-4(XY’-Y)=0$
$Y’^2-4XY’+4Y=0$

ここで，式を $Y$ の式に合わせていきます。

⑤，⑥を代入して

$\cfrac{a^2}{Y^2}-4\cdot\Big(\cfrac{1}{2a}Y^2+\cfrac{3a}{4}\Big)\cdot\cfrac{a}{Y}+4Y=0$
$\cfrac{a^2}{Y^2}-\cfrac{4aY^2}{2aY}-\cfrac{12a^2}{4Y}+4Y=0$
$\cfrac{a^2}{Y^2}-2Y-\cfrac{3a^2}{Y}+4Y=0$

式に $Y^2$ をかけると

$a^2-2Y^3-3a^2Y+4Y^3=0$
$2Y^3-3a^2Y+a^2=0$

次に，式を $Y$ の式とみなして，条件を満たす $Y$ が 3 つ存在する場合を考えます。ここで，思い出すと良いのが定数分離です。

移項して

$-2Y^3+3a^2Y=a^2$ 

$f(x)=-2Y^3+3a^2Y$ とすると

$f'(x)=-6Y^2+3a^2$

$-6Y^2+3a^2=0$ のとき

$6Y^2=3a^2$
$Y^2=\cfrac{a^2}{2}$
$Y=\pm\sqrt{\cfrac{a^2}{2}}=\pm\cfrac{a}{\sqrt{2}}$

グラフは $\cfrac{a}{\sqrt{2}}$ と $-\cfrac{a}{\sqrt{2}}$ で極値をとる。

$f\Big(\cfrac{a}{\sqrt{2}}\Big)=-2\Big(\cfrac{a}{\sqrt{2}}\Big)^3+\cfrac{3a^3}{\sqrt{2}}$
$=-\cfrac{a^3}{\sqrt{2}}+\cfrac{3a^3}{\sqrt{2}}=\cfrac{2a^3}{\sqrt{2}}$
$f\Big(-\cfrac{a}{\sqrt{2}}\Big)=-2\Big(-\cfrac{a}{\sqrt{2}}\Big)^3-\cfrac{3a^3}{\sqrt{2}}$
$=\cfrac{a^3}{\sqrt{2}}-\cfrac{3a^3}{\sqrt{2}}=-\cfrac{2a^3}{\sqrt{2}}$

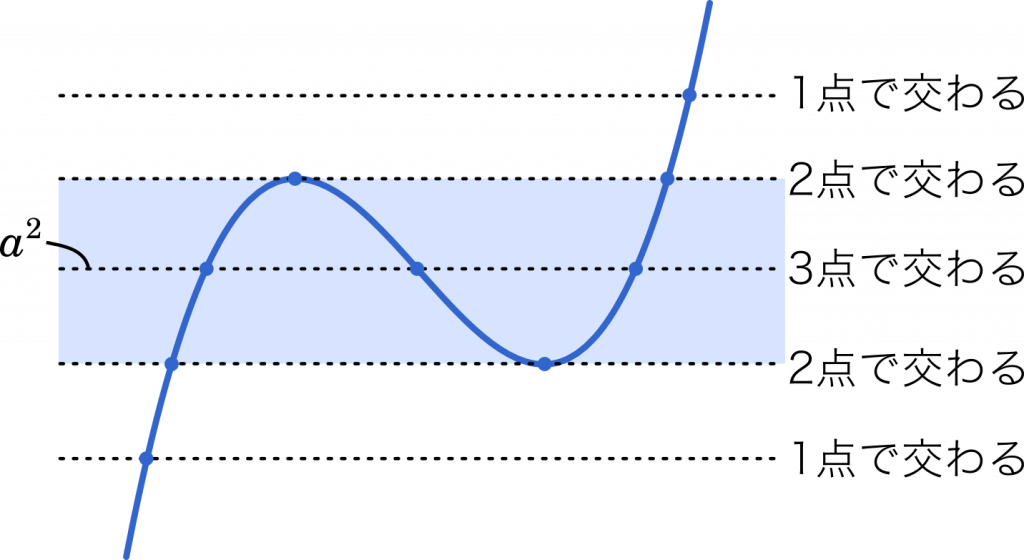
最後に見落としてはいけないのは，$a$ はプラスのときとマイナスのときがあるので，分けて考える必要があることです。

(i) $a$ ＞ $0$ のとき

$-\cfrac{2a^3}{\sqrt{2}}$ ＜ $\cfrac{2a^3}{\sqrt{2}}$ だから

$-\cfrac{2a^3}{\sqrt{2}}$ ＜ $a^2$ ＜ $\cfrac{2a^3}{\sqrt{2}}$

$-\cfrac{2a^3}{\sqrt{2}}$ ＜ $a^2$
$-\cfrac{a^3}{a^2}$ ＜ $\cfrac{\sqrt{2}}{2}$
$a$ ＞ $-\cfrac{\sqrt{2}}{2}$

また

$a^2$ ＜ $\cfrac{2a^3}{\sqrt{2}}$
$\cfrac{\sqrt{2}}{2}$ ＜ $\cfrac{a^3}{a^2}$
$\cfrac{\sqrt{2}}{2}$ ＜ $a$

まとめると $\cfrac{\sqrt{2}}{2}$ ＜ $a$

(ii) $a$ ＜ 0 のとき

$\cfrac{2a^3}{\sqrt{2}}$ ＜ $-\cfrac{2a^3}{\sqrt{2}}$ だから

$\cfrac{2a^3}{\sqrt{2}}$ ＜ $a^2$ ＜ $-\cfrac{2a^3}{\sqrt{2}}$

不等式を分けると

$\cfrac{2a^3}{\sqrt{2}}$ ＜ $a^2$
$\cfrac{a^3}{a^2}$ ＜ $\cfrac{\sqrt{2}}{2}$
$a$ ＜ $\cfrac{\sqrt{2}}{2}$

また

$a^2$ ＜ $-\cfrac{2a^3}{\sqrt{2}}$
$\cfrac{\sqrt{2}}{2}$ ＜ $-\cfrac{a^3}{a^2}$
$-\cfrac{\sqrt{2}}{2}$ ＞ $a$

まとめると $a$ ＜ $-\cfrac{\sqrt{2}}{2}$

したがって $a$ ＜ $-\cfrac{\sqrt{2}}{2}$，$\cfrac{\sqrt{2}}{2}$ ＜ $a$ （答え）