【数III】複素数平面と階差数列の一般項を組み合わせる(千葉大2020第8問)

複素数平面上で複素数 $0$，$\sqrt{3}$，$\sqrt{3}+i$ を表す点をそれぞれ $\text{A}_1$，$\text{B}_0$，$\text{B}_1$ とする。正の整数 $n$ に対して，点 $\text{A}_{n+1}$ は線分 $\text{A}_n\text{B}_n$ の中点とし，点 $\text{B}_{n+1}$ は直線 $\text{A}_n\text{B}_n$ の中点とし，点 $\text{B}_{n+1}$ は直線 $\text{A}_n\text{B}_n$ に関して点 $\text{B}_{n-1}$ の反対側にあり，三角形 $\text{A}_{n+1}\text{B}_n\text{B}_{n+1}$ が三角形 $\text{A}_1\text{B}_0\text{B}_1$ と相似になるものとする。点 $\text{A}_n$ ($n=1,2,3,\cdots$) が表す複素数を $Z_n$ とする。

(1) 複素数 $z_3$ を求めよ。
(2) 複素数 $z_6$ を求めよ。
(3) 正の整数 $m$ に対して，複素数 $z_{6m}$ の実部と虚部をそれぞれ求めよ。

図を描いて法則性を見つける

(1)から進めます。

はじめは作図ができるかどうかが勝負だろうね。
$\text{B}_{n+1}$ は $\text{B}_{n-1}$ と線対称ということ？
ではない。あくまで直線の反対側であって，反対側のどこか。
って，どこ？
もとの三角形と新しく作った三角形が相似だと言ってる。日本語に注意して作図するとこうなる。

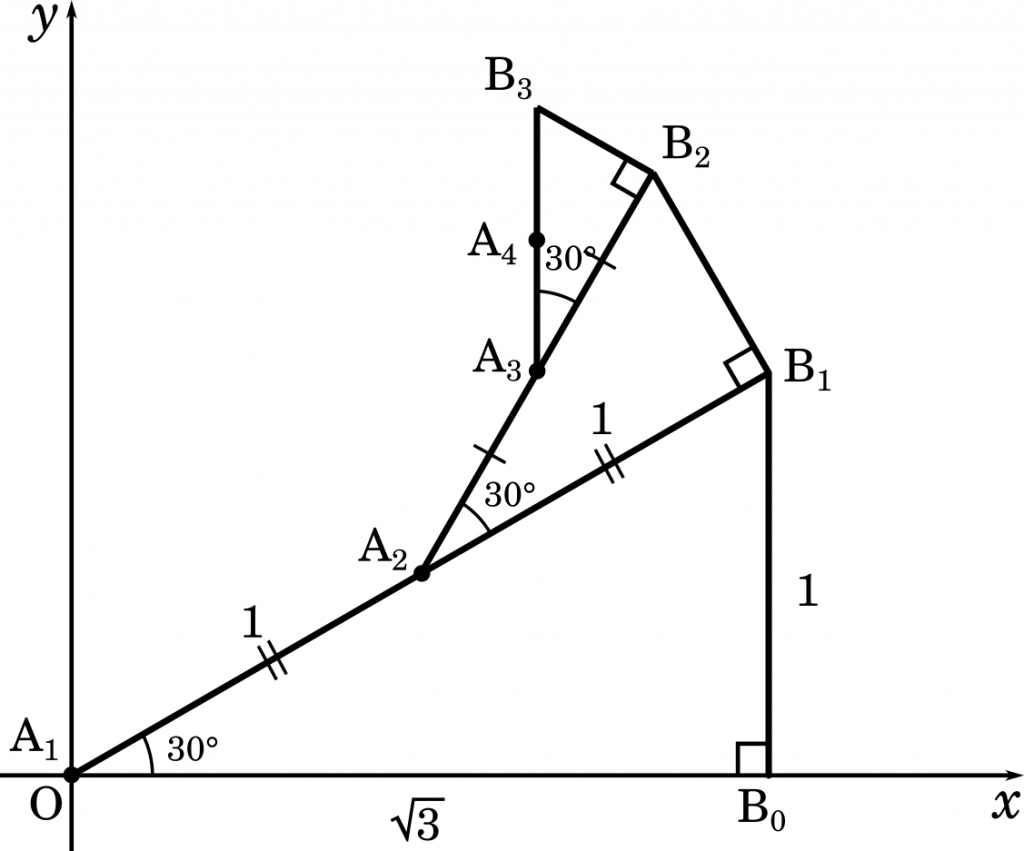
できあがる三角形は $1:2:\sqrt{3}$ の三角形です。したがって，偏角は 30° となります。

図の中から法則性見つかる？
んー，三角形が回転しながら小さくなってますよね。
それそれ。そこに気づいたら，数式で表すことを考える。

$\text{A}_2$ は $\text{B}_0$ を 30° 回転して，長さを $\cfrac{1}{\sqrt{3}}$ にしたものです。 $\text{A}_1\text{A}_2$ と $\text{A}_2\text{B}_1$ は同じ長さなので，$\text{A}_1\text{A}_2$ を 30° 回転して，長さを $\cfrac{1}{\sqrt{3}}$ にしたものが，$\text{A}_2\text{A}_3$ になると言えます。

ただし，スタート地点を $\text{A}_2$ に持っていく必要がある。

複素数平面において，極座標をかけ算することで点を回転させることができます。30° 回転を繰り返していくので，これをいったん $\alpha$ とすると計算が楽になります。

$\cos 30\degree+i\sin 30\degree=\cfrac{\sqrt{3}+i}{2}=\alpha$ とする。

$z_2=\sqrt{3}\cdot\cfrac{1}{\sqrt{3}}\space\alpha=\alpha$

長さを $\cfrac{1}{\sqrt{3}}$ にして，30° 回転させることを式にすると，上のようになる。

$z_3$ は $\text{A}_3$ のことですが，$z_2$ を長さ $\cfrac{1}{\sqrt{3}}$ にして 30° 回転させ，$z_2$ を加えて平行移動することで $z_3$ になります。

$z_3=z_2\cdot\cfrac{1}{\sqrt{3}}\space\alpha+z_2$
$=\alpha\cdot\cfrac{\alpha}{\sqrt{3}}+\cfrac{\alpha}{\sqrt{3}}$
$=\cfrac{1}{\sqrt{3}}\Big(\cfrac{\sqrt{3}+i}{2}\Big)^2+\cfrac{\sqrt{3}+i}{2}$
$=\cfrac{3+2\sqrt{3}i-1}{4\sqrt{3}}+\cfrac{\sqrt{3}+i}{2}$
$=\cfrac{1+\sqrt{3}i}{2\sqrt{3}}+\cfrac{\sqrt{3}+i}{2}$
$=\cfrac{1+\sqrt{3}i+3+\sqrt{3}i}{2\sqrt{3}}$
$=\cfrac{4+2\sqrt{3}i}{2\sqrt{3}}$
$=\cfrac{2+\sqrt{3}i}{\sqrt{3}}$
$=\cfrac{2\sqrt{3}+3i}{3}$　（答え）

法則性を見抜いて階差数列の一般項を求める

(2)に進みます。

$z_4$ を考えてみると

$z_4=(z_3-z_2)\cfrac{1}{\sqrt{3}}\alpha+z_3$

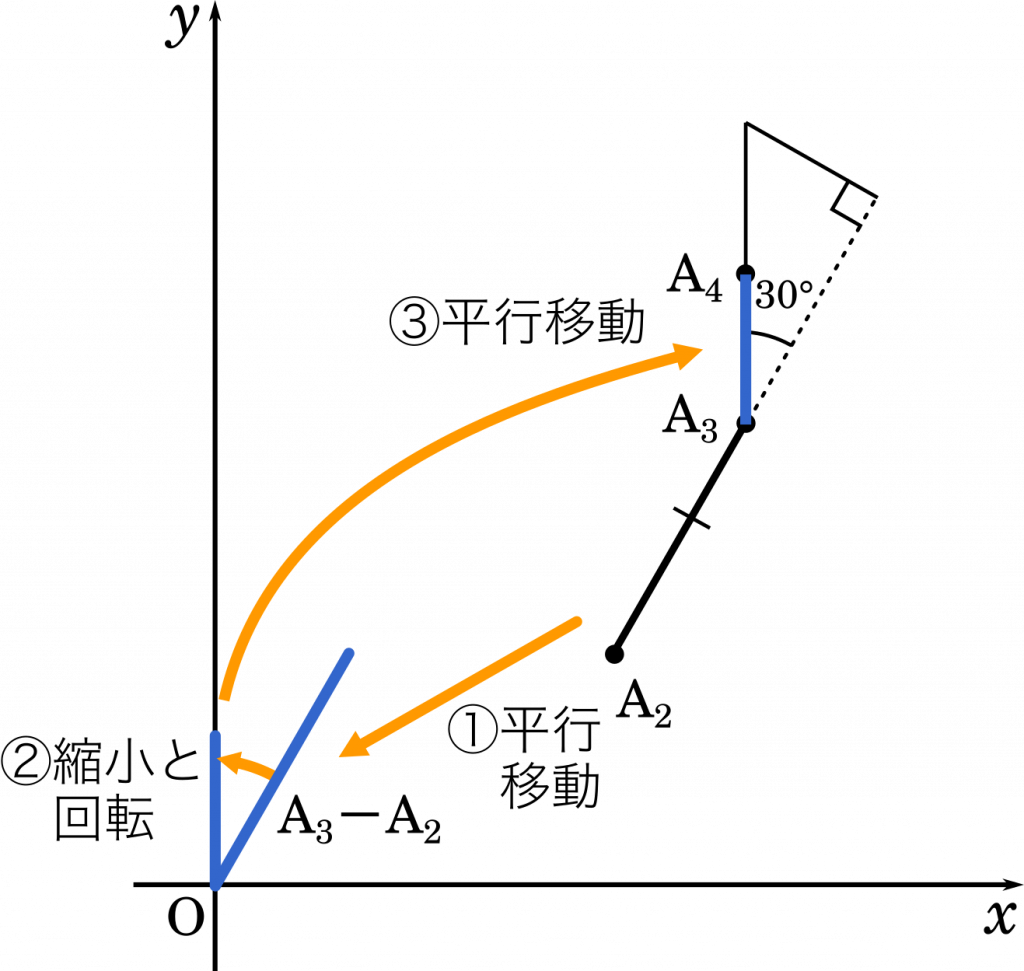
まず，$z_3-z_2$ と引き算することで $\text{A}_2\text{A}_3$ を原点に平行移動します。そして，$\cfrac{1}{\sqrt{3}}$ をかけて長さを縮小，$\alpha$ をかけて回転させます。最後に $z_3$ を足して目的の場所に平行移動させます。

複素数平面で拡大縮小や回転をするときにはいったん始点を原点に戻した上で行う。

移項すると

$z_4-z_3=(z_3-z_2)\cfrac{\alpha}{\sqrt{3}}$

式を漸化式としてみると，それぞれの項の差は上のようになる。
項どうしの差に $\cfrac{\alpha}{\sqrt{3}}$ をかけたものが次の差になるのか。

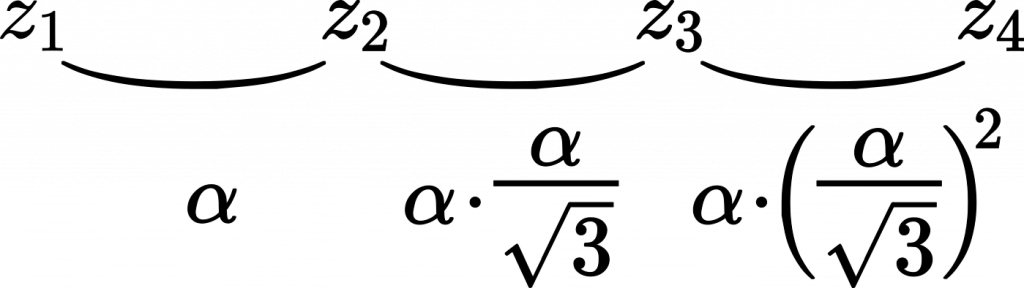
つまり，$z_n$ は階差数列で，階差部分が初項 $\alpha$，公比 $\cfrac{1}{\sqrt{3}}$ の等比数列になっているということです。

たとえば，$z_4=z_1+\alpha+\alpha\cdot\cfrac{\alpha}{\sqrt{3}}+\alpha\space\Big(\cfrac{\alpha}{\sqrt{3}}\Big)^2$ という具合に，初項に階差数列の和を足していけば数列の値を求めることができます。

階差数列と一般項の公式
数列 $\{a_n\}$ の階差数列を $\{b_n\}$ とすると
$\displaystyle a_n=a_1+\sum_{k=1}^{n-1} b_k$　（$n$ ≧ $2$）

$z_1=0$ に注意して，一般項は

$\displaystyle z_n=\sum_{k=1}^{n-1} \alpha\Big(\cfrac{\alpha}{\sqrt{3}}\Big)^{k-1}$ （$n$ ≧ $2$）

これは，等比数列の和を求めるということです。

等比数列の和の公式　$S_n=\cfrac{a(1-r^n)}{1-r}$　（初項 $a$，公比 $r$）

$z_n=\cfrac{\alpha\Big\{1-\Big(\cfrac{\alpha}{\sqrt{3}}\Big)^{n-1}\Big\}}{1-\cfrac{\alpha}{\sqrt{3}}}$

作図がうまくいった時点で，これ等比数列じゃね？ってのがひらめくといいね。着地点が分かればあとは何とかなると思う。
これでようやく本題に入れる。

$z_6=\cfrac{\alpha\Big\{1-\Big(\cfrac{\alpha}{\sqrt{3}}\Big)^5\Big\}}{1-\cfrac{\alpha}{\sqrt{3}}}$
$=\cfrac{\alpha-\cfrac{\alpha^6}{9\sqrt{3}}}{1-\cfrac{\alpha}{\sqrt{3}}}$
$=\cfrac{9\sqrt{3}\alpha-\alpha^6}{9\sqrt{3}-9\alpha}$

ここで，ド・モアブルの定理より
$\alpha^6=(\cos30\degree+i\sin30\degree)^6$
$=\cos180\degree+i\sin180\degree=-1$

したがって，与式は

$=\cfrac{9\sqrt{3}\alpha+1}{9(\sqrt{3}-\alpha)}$
$=\cfrac{9\sqrt{3}\cdot\cfrac{\sqrt{3}+i}{2}+1}{9\Big(\sqrt{3}-\cfrac{\sqrt{3}+i}{2}\Big)}$
$=\cfrac{9\sqrt{3}(\sqrt{3}+i)+2}{9(2\sqrt{3}-\sqrt{3}-i)}$
$=\cfrac{27+9\sqrt{3}i+2}{9(\sqrt{3}-i)}$
$=\cfrac{(29+9\sqrt{3}i)(\sqrt{3}+i)}{9(\sqrt{3}-i)(\sqrt{3}+i)}$
$=\cfrac{29\sqrt{3}+29i+27i-9\sqrt{3}}{9(3+1)}$
$=\cfrac{20\sqrt{3}+56i}{36}$
$=\cfrac{5\sqrt{3}+14i}{9}$　（答え）

実部と虚部を求める

(3)に進みます。

(2)で一般項は

$z_n=\cfrac{\alpha\Big\{1-\Big(\cfrac{\alpha}{\sqrt{3}}\Big)^{n-1}\Big\}}{1-\cfrac{\alpha}{\sqrt{3}}}$ （$n$ ≧ $2$）

だったので，$z_{6m}$ を求めればよいことになります。

計算するだけ？
計算するだけ。ただ，(2)も(3)も計算ミス無しで突破するの実際かなりタイヘンだと思うの。計算力鍛える特訓だと思って頑張って。

$z_{6m}=\cfrac{\alpha\Big\{1-\Big(\cfrac{\alpha}{\sqrt{3}}\Big)^{6m-1}\Big\}}{1-\cfrac{\alpha}{\sqrt{3}}}$
$=\cfrac{\alpha-\alpha\Big(\cfrac{\alpha}{\sqrt{3}}\Big)^{6m-1}}{1-\cfrac{\alpha}{\sqrt{3}}}$

ここで

$\alpha\Big(\cfrac{\alpha}{\sqrt{3}}\Big)^{6m-1}=\alpha\Big(\cfrac{\alpha}{\sqrt{3}}\Big)^{6m}\cdot\Big(\cfrac{\alpha}{\sqrt{3}}\Big)^{-1}$
$=\alpha\Big(\cfrac{\alpha}{\sqrt{3}}\Big)^{6m}\cdot\cfrac{\sqrt{3}}{\alpha}$
$=\sqrt{3}\Big(\cfrac{\alpha}{\sqrt{3}}\Big)^{6m}$
$=\sqrt{3}\cdot\cfrac{\alpha^{6m}}{(\sqrt{3})^{6m}}$
$=\sqrt{3}\cdot\cfrac{(-1)^m}{27^m}$
$=\sqrt{3}\Big(-\cfrac{1}{27}\Big)^m$

よって，与式は

$=\cfrac{\alpha-\sqrt{3}\Big(-\cfrac{1}{27}\Big)^m}{1-\cfrac{\alpha}{\sqrt{3}}}$
$=\cfrac{\sqrt{3}\alpha-3\Big(-\cfrac{1}{27}\Big)^m}{\sqrt{3}-\alpha}$
$=\cfrac{\sqrt{3}\cfrac{\sqrt{3}+i}{2}-3\Big(-\cfrac{1}{27}\Big)^m}{\sqrt{3}-\cfrac{\sqrt{3}+i}{2}}$
$=\cfrac{\sqrt{3}(\sqrt{3}+i)-6\Big(-\cfrac{1}{27}\Big)^m}{2\sqrt{3}-\sqrt{3}-i}$
$=\cfrac{3+\sqrt{3}i-6\Big(-\cfrac{1}{27}\Big)^m}{\sqrt{3}-i}$
$=\cfrac{\Big\{(3+\sqrt{3}i)-6\Big(-\cfrac{1}{27}\Big)^m\Big\}(\sqrt{3}+i)}{(\sqrt{3}-i)(\sqrt{3}+i)}$
$=\cfrac{\sqrt{3}(3+\sqrt{3}i)+(3+\sqrt{3}i)i-6\sqrt{3}\Big(-\cfrac{1}{27}\Big)^m-6\Big(-\cfrac{1}{27}\Big)^m i}{3+1}$
$=\cfrac{1}{4}\Big\{3\sqrt{3}+3i+3i-\sqrt{3}-6\sqrt{3}\Big(-\cfrac{1}{27}\Big)^m-6\Big(-\cfrac{1}{27}\Big)^m i\Big\}$
$=\cfrac{1}{4}\Big\{2\sqrt{3}-6\sqrt{3}\Big(-\cfrac{1}{27}\Big)^m+6i-6\Big(-\cfrac{1}{27}\Big)^m i\Big\}$

したがって，実部は

$\cfrac{1}{4}\Big\{2\sqrt{3}-6\sqrt{3}\Big(-\cfrac{1}{27}\Big)^m\Big\}$
$=\cfrac{\sqrt{3}}{2}\Big\{1-3\Big(-\cfrac{1}{27}\Big)^m\Big\}$　（答え）

また，虚部は

$\cfrac{1}{4}\Big\{6-6\Big(-\cfrac{1}{27}\Big)^m\Big\}$
$=\cfrac{3}{2}\Big\{1-\Big(-\cfrac{1}{27}\Big)^m\Big\}$　（答え）

SNSでシェア

mm参考書 2019-2023