【数Ⅲ複素数平面】z の n 乗根の求め方


$z$ の $n$ 乗を求める問題
問題 $z^3=1$ のとき、$z$ を求めよ。
$z=r(\cos\theta+i\sin\theta)$ $(0\leqq\theta\leqq 2\pi)$
$z^3=r^3(\cos\theta+i\sin\theta)^3$
ド・モアブルの定理より
$z^3=r^3(\cos 3\theta+i\sin 3\theta)$
$1$ を極形式で表すと $\cos 0+i\sin 0$
よって
$\cos 0+i\sin 0=r^3(\cos 3\theta+i\sin 3\theta)$
両辺を比べると
$r=1$、$3\theta=0+2k\pi$ $(0\leqq 3\theta\leqq 6\pi)$
$\displaystyle \theta=\frac{2k\pi}{3}$ $(0\leqq\theta\leqq 2\pi)$
したがって
$\displaystyle z_0=\cos 0+i\sin 0=1$
$\displaystyle z_1=\cos\frac{2\pi}{3}+i\sin\frac{2\pi}{3}=-\frac{1}{2}+\frac{\sqrt{3}}{2}i$
$\displaystyle z_2=\cos\frac{4\pi}{3}+i\sin\frac{4\pi}{3}=-\frac{1}{2}-\frac{\sqrt{3}}{2}i$
ド・モアブルの定理


$z=r(\cos\theta+i\sin\theta)$
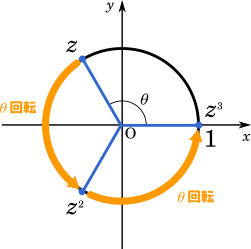



両辺を3乗して
$z^3=r^3(\cos\theta+i\sin\theta)^3$


$$(\cos\theta+i\sin\theta)^n=\cos n\theta+i\sin n\theta$$
よって
$z^3=r^3(\cos 3\theta+i\sin 3\theta)$
係数を比較する



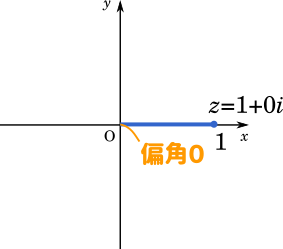

$1=1\times(\cos 0+i\sin 0)$

両辺を比べると
$r=1$、$3\theta=0+2k\pi$ $(0\leqq 3\theta\leqq 6\pi)$



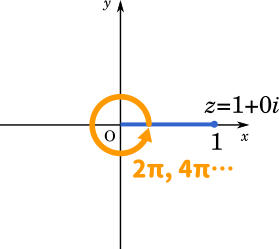

$\displaystyle \theta=\frac{2k\pi}{3}$ $(0\leqq\theta\leqq 2\pi)$
$\theta$ の範囲から言うと、$k=0,1,2$で成り立つから、順番に当てはめていくと
$\displaystyle z_0=\cos 0+i\sin 0=1$
$\displaystyle z_1=\cos\frac{2\pi}{3}+i\sin\frac{2\pi}{3}=-\frac{1}{2}+\frac{\sqrt{3}}{2}i$
$\displaystyle z_2=\cos\frac{4\pi}{3}+i\sin\frac{4\pi}{3}=-\frac{1}{2}-\frac{\sqrt{3}}{2}i$


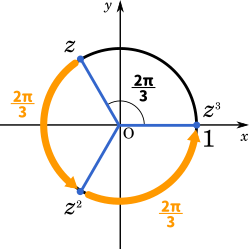


範囲の考えかた


$\displaystyle z_3=\cos\frac{6\pi}{3}+i\sin\frac{6\pi}{3}=\cos 2\pi+i\sin 2\pi=1$
$\displaystyle z_4=\cos\frac{8\pi}{3}+i\sin\frac{8\pi}{3}=\cos\frac{2\pi}{3}+i\sin\frac{2\pi}{3}=-\frac{1}{2}+\frac{\sqrt{3}}{2}i$
$\displaystyle z_5=\cos\frac{10\pi}{3}+i\sin\frac{10\pi}{3}=\cos\frac{4\pi}{3}+i\sin\frac{4\pi}{3}=-\frac{1}{2}-\frac{\sqrt{3}}{2}i$


1の6乗根
問題 $z^6=1$ のとき、$z$ を求めよ。

$z_0=\cos 0+i\sin 0=1$
$\displaystyle z_1=\cos\frac{\pi}{3}+i\sin\frac{\pi}{3}=\frac{1}{2}+\frac{\sqrt{3}}{2}i$
$\displaystyle z_2=\cos\frac{2\pi}{3}+i\sin\frac{2\pi}{3}=-\frac{1}{2}+\frac{\sqrt{3}}{2}i$
$\displaystyle z_3=\cos\pi+i\sin\pi=-1$
$\displaystyle z_4=\cos\frac{4\pi}{3}+i\sin\frac{4\pi}{3}=-\frac{1}{2}-\frac{\sqrt{3}}{2}i$
$\displaystyle z_5=\cos\frac{5\pi}{3}+i\sin\frac{5\pi}{3}=\frac{1}{2}-\frac{\sqrt{3}}{2}i$
SNSでシェア