【数Ⅲ複素数平面】複素数同士が垂直になるとき 複素数と極形式は同じことだと理解する
問題 任意の自然数 $n$ に対して、複素数 $z_n$ を $z_n=(\sqrt{3}+i)^n$ で定義する。
複素数平面上で $z_{3n}$、$z_{3(n+1)}$、$z_{3(n+2)}$ が表す3点をそれぞれA、B、Cとするとき、∠ABCは直角であることを証明せよ。(島根大)

垂直条件が成り立つ仕組み
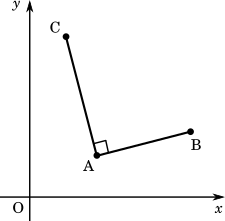
複素数平面上の点A$(\alpha)$、B$(\beta)$、C$(\gamma)$ において、
$$\displaystyle\frac{\gamma-\alpha}{\beta-\alpha}$$
が純虚数であるとき、AB⊥AC が成り立つ。




商の公式
$\alpha=r_1(\cos\theta_1+i\sin\theta_1),\beta=r_2(\cos\theta_2+i\sin\theta_2)$ のとき
$$\displaystyle \frac{\alpha}{\beta}=\frac{r_1}{r_2}\{\cos(\theta_1-\theta_2)+i\sin(\theta_1-\theta_2)\}$$


複素数と極形式

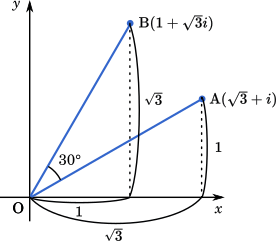


$\alpha=2(\cos 30\degree+i\sin 30\degree)$
$\beta=2(\cos 60\degree+i\sin 60\degree)$
$\displaystyle\frac{\beta}{\alpha}=\frac{2}{2}\{\cos(60\degree-30\degree)+i\sin(60\degree-30\degree)$
$\displaystyle=\cos 30\degree+i\sin 30\degree$
$\displaystyle=\frac{\sqrt{3}}{2}+\frac{1}{2}i$




$\displaystyle\frac{\beta}{\alpha}=\frac{1+\sqrt{3}i}{\sqrt{3}+i}$
分母を有理化して
$\displaystyle=\frac{(1+\sqrt{3}i)(\sqrt{3}-i)}{(\sqrt{3}+i)(\sqrt{3}-i)}$
$\displaystyle=\frac{\sqrt{3}-i+3i+\sqrt{3}}{3+1}$
$\displaystyle=\frac{2\sqrt{3}+2i}{4}$
$\displaystyle=\frac{\sqrt{3}}{2}+\frac{1}{2}i$






複素数平面のありがたさを実感してみる

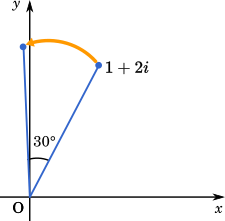



$\displaystyle (1+2i)(\frac{\sqrt{3}}{2}+\frac{1}{2}i)$
$\displaystyle =\frac{\sqrt{3}}{2}+\frac{1}{2}i+\sqrt{3}i-1$
$\displaystyle =\frac{\sqrt{3}-2}{2}+\frac{1+2\sqrt{3}}{2}i$


垂直イコール純虚数の意味




公式を用いて偏角を考える
問題 任意の自然数 $n$ に対して、複素数 $z_n$ を $z_n=(\sqrt{3}+i)^n$ で定義する。
複素数平面上で $z_{3n}$、$z_{3(n+1)}$、$z_{3(n+2)}$ が表す3点をそれぞれA、B、Cとするとき、∠ABCは直角であることを証明せよ。(島根大)



$z_{3n}=(\sqrt{3}+i)^{3n}$

$=\{(\sqrt{3}+i)^3\}^n$
$=(3\sqrt{3}+9i-3\sqrt{3}-i)^n$
$=(8i)^n$
よって
$z_{3(n+1)}=(\sqrt{3}+i)^{3(n+1)}=\{(\sqrt{3}+i)^3\}^{n+1}=(8i)^{n+1}$
$z_{3(n+2)}=(\sqrt{3}+i)^{3(n+2)}=\{(\sqrt{3}+i)^3\}^{n+2}=(8i)^{n+2}$
$\displaystyle \frac{z_{3(n+2)}-z_{3(n+1)}}{z_{3n}-z_{3(n+1)}}=\frac{(8i)^{n+2}-(8i)^{n+1}}{(8i)^n-(8i)^{n+1}}$
$\displaystyle =\frac{(8i)^{n+1}(8i-1)}{(8i)^n(1-8i)}$
$\displaystyle =\frac{-(8i)^{n+1}(1-8i)}{(8i)^n(1-8i)}$
$\displaystyle =-8i$
したがって、純虚数であるから∠ABCは直角である。

SNSでシェア