【数III積分】円環体（ドーナツ型）の体積の求め方

[問題] $x^2+(y-2)^2=1$ が $x$ 軸の周りに 1 回転してできる回転体の体積を求めよ。

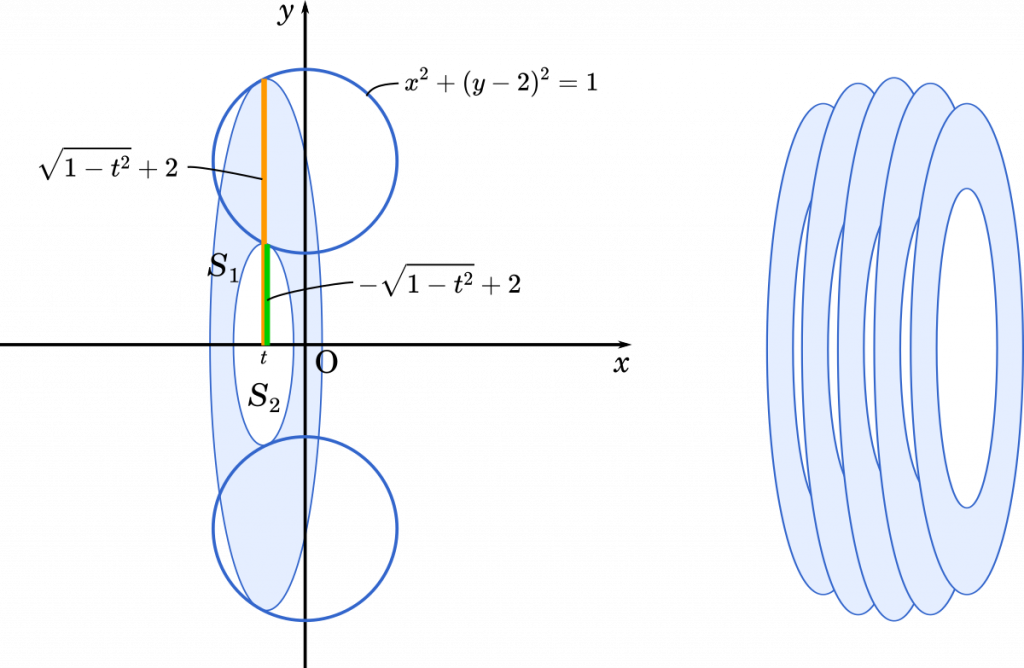
考え方としては，大きな円から小さな円の面積を引くことでドーナツの面積を求め，それを積分で積み上げることで体積を求めます。

まず，$x=t$ として，式を変形します。

$t^2+(y-2)^2=1$
$(y-2)^2=1-t^2$
$y-2=\pm\sqrt{1-t^2}$
$y=\pm\sqrt{1-t^2}+2$

プラスとマイナスの 2 つが出てきますが，これは 1 つの $t$ の値につき，円の上と下の 2 点があるからです。これらのうち，プラスの方が大きな円の半径，マイナスのほうが小さな円の半径となります。

円の面積は $\pi r^2$ だから，大きな円の面積を求めると

$S_1=\pi(\sqrt{1-t^2}+2)^2$
$=\pi(1-t^2+4\sqrt{1-t^2}+4)$
$=\pi(-t^2+4\sqrt{1-t^2}+5)$

小さな円の面積は

$S_2=\pi(-\sqrt{1-t^2}+2)^2$
$=\pi(1-t^2-4\sqrt{1-t^2}+4)$
$=\pi(-t^2-4\sqrt{1-t^2}+5)$

大きな円の面積から小さな円の面積を引けば，ドーナツの面積になります。

$S_1-S_2$
$=\pi(-t^2+4\sqrt{1-t^2}+5+t^2+4\sqrt{1-t^2}-5)$
$=8\sqrt{1-t^2}\pi$

$t$ の範囲は $-1$ から $1$ までだから，積分をして体積を求めます。

$\displaystyle V=8\pi\int_{-1}^1 \sqrt{1-t^2}\space dt$

$t=\sin\theta$ とすると

$dt=\cos\theta\space d\theta$

$\def\arraystretch{1.5}\begin{array}{c|c}t&-1\rightarrow 1\\\hline\theta&-\frac{\pi}{2}\rightarrow\frac{\pi}{2}\end{array}$

よって

$\displaystyle V=8\pi\int_{\small{-\frac{\pi}{2}}}^{\small{\frac{\pi}{2}}}\sqrt{1-\sin^2\theta}\cos\theta\space d\theta$
$\displaystyle =8\pi\int_{\small{-\frac{\pi}{2}}}^{\small{\frac{\pi}{2}}}\cos^2\theta\space d\theta$

$\cos^2\theta$ は偶関数だから

$\displaystyle =16\pi\int_0^{\small{\frac{\pi}{2}}}\cos^2\theta\space d\theta$

半角の公式 $\cos^2 x=\cfrac{1+\cos2x}{2}$ を用いて

$\displaystyle =16\pi\int_0^{\small{\frac{\pi}{2}}}\cfrac{1+\cos2\theta}{2}\space d\theta$
$\displaystyle =8\pi\int_0^{\small{\frac{\pi}{2}}}1+\cos2\theta\space d\theta$
$=8\pi\Big[\theta-\cfrac{1}{2}\sin2\theta\Big]_0^{\small{\frac{\pi}{2}}}$
$=8\pi\Big(\cfrac{\pi}{2}-\cfrac{1}{2}\cdot0\Big)$
$=4\pi^2$　（答え）