ド・モアブルの定理を用いて共役複素数を整理する(千葉大2016第9問)

因数定理を用いて方程式を因数分解する

(1)から進めます。

まず，$\cfrac{2\pi}{7}$ は 7 倍すると $2\pi$ となります。

ド・モアブルの定理より

$z^7=\Big(\cos\cfrac{2\pi}{7}+i\sin\cfrac{2\pi}{7}\Big)^7$
$=\cos\Big(7\cdot\cfrac{2\pi}{7}\Big)+i\sin\Big(7\cdot\cfrac{2\pi}{7}\Big)$
$=\cos 2\pi+i\sin2\pi=1$

次に，$z^7=1$ を移項して

$z^7-1=0$ ・・・①

方程式の解の一つは 1 だから，因数定理より式は $z-1$ で割り切れる。

組立除法を用いて

$\begin{aligned}z^7&&z^6&&z^5&&z^4&&z^3&&z^2&&z^1&&&&|\underline{1}\\1&&0&&0&&0&&0&&0&&0&&-1\\&&1&&1&&1&&1&&1&&1&&1\\\hline 1&&1&&1&&1&&1&&1&&1&&0\\z^6&&z^5&&z^4&&z^3&&z^2&&z^1\end{aligned}$

よって①は

$(z-1)(z^6+z^5+z^4+z^3+z^2+z+1)=0$

と因数分解できる。

ここで，恒等式が成立するのは $z=1$ か $z^6+z^5+z^4+z^3+z^2+z+1=0$ のときです。

しかし，もともと問題文で $z=\cos\cfrac{2\pi}{7}+i\sin\cfrac{2\pi}{7}$ となっていたので，$z$ ≠ $1$ です。したがって

$z^6+z^5+z^4+z^3+z^2+z+1=0$
$z+z^2+z^3+z^4+z^5+z^6=-1$ （答え）

共役複素数との相互関係

(2)に進みます。

$\alpha=z+z^2+z^4$ だから
$\bar{\alpha}=\bar{z}+\overline{z^2}+\overline{z^4}$

たとえば

$z=\cos\cfrac{2\pi}{7}+i\sin\cfrac{2\pi}{7}$
$\bar{z}=\cos\cfrac{2\pi}{7}-i\sin\cfrac{2\pi}{7}$
$=\cos\Big(-\cfrac{2\pi}{7}\Big)+i\sin\Big(-\cfrac{2\pi}{7}\Big)$
$=z^6$

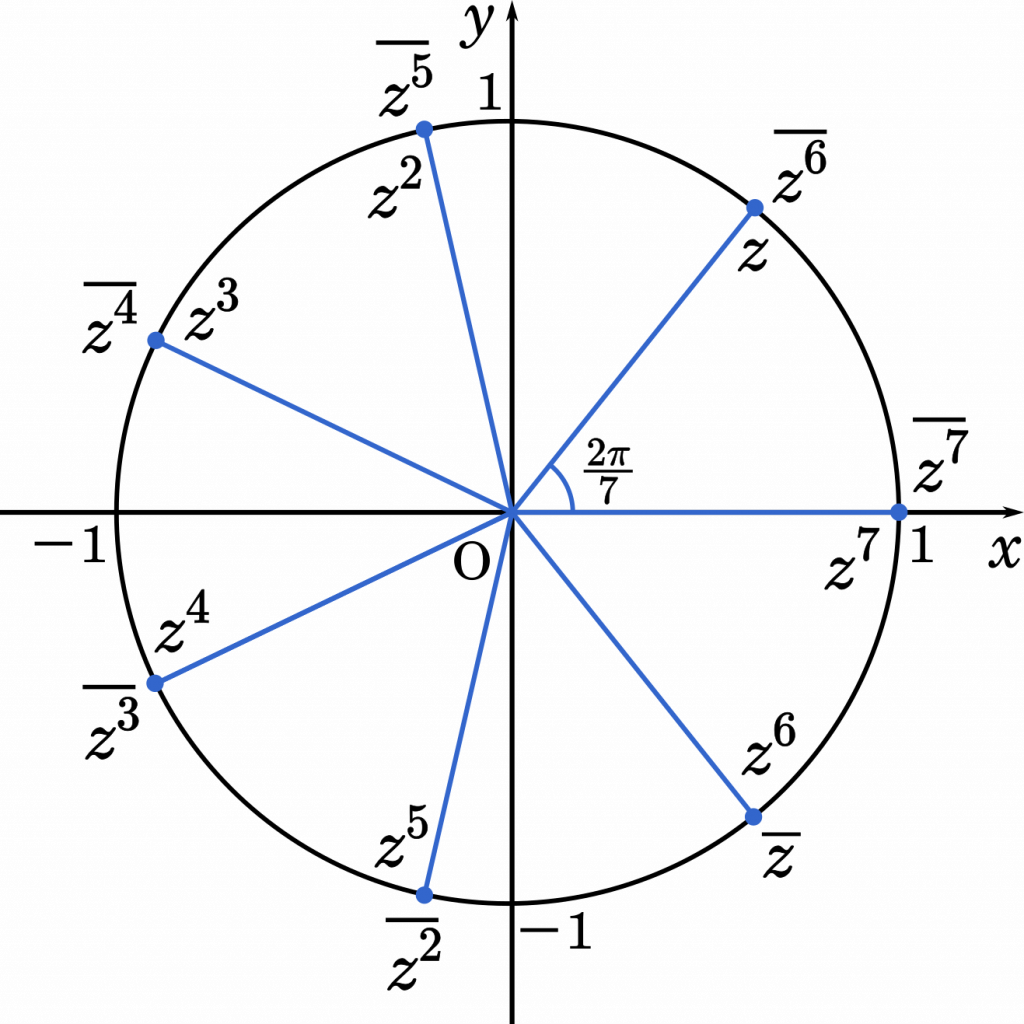
ド・モアブルの定理から言えば，複素数を 2 乗することと偏角を 2 倍することは同じであり，3 乗，4 乗・・・とすれば偏角 3 倍，4 倍・・・となります。

また，共役な複素数では偏角が反対回りで進んでいきます。図を見れば，$z^2=\overline{z^5}$，$\overline{z^2}=z^5$ など，共役な複素数との間にさまざまな相互関係があることが分かります。

これらを使って，式を作っていきます。

$\bar{\alpha}=\bar{z}+\overline{z^2}+\overline{z^4}$
$=z^6+z^5+z^3$

したがって

$\alpha+\bar{\alpha}=z+z^2+z^3+z^4+z^5+z^6=-1$ （答え)

次に $\alpha\bar{\alpha}$ を求めます。

$\alpha\bar{\alpha}=(z+z^2+z^4)(\bar{z}+\overline{z^2}+\overline{z^4})$
$=z\bar{z}+z\overline{z^2}+z\overline{z^4}+z^2\bar{z}+z^2\overline{z^2}+z^2\overline{z^4}+z^4\bar{z}+z^4\overline{z^2}+z^4\overline{z^4}$

$|z|=1$ だから $z\bar{z}=|z|^2=1$ より

$z\overline{z^2}=z\bar{z}\cdot\bar{z}=|z|^2\bar{z}=\bar{z}$ のように計算していくと
$=1+\bar{z}+\overline{z^3}+z+1+\overline{z^2}+z^3+z^2+1$

$=1+z^6+z^4+z+1+z^5+z^3+z^2+1$
$=z+z^2+z^3+z^4+z^5+z^6+3$

(1)より $z+z^2+z^3+z^4+z^5+z^6=-1$ を用いて

$=-1+3=2$ （答え）

最後に $\alpha$ を求めます。2 数の和と積を求めたので解と係数の関係を使うとよいでしょう。

$\alpha$，$\bar{\alpha}$ を方程式の解とみなすと
$\alpha+\bar{\alpha}=-1$，$\alpha\bar{\alpha}=2$ より
$x^2+x+2=0$
$x=\cfrac{-1\pm\sqrt{1-8}}{2}$
$=\cfrac{-1\pm\sqrt{7}i}{2}$

したがって

$\alpha=\cfrac{-1+\sqrt{7}i}{2}$　（答え）

前の問題で用いた形に式を合わせていく

(3)に進みます。

(2)でやった共役複素数の関係と $\alpha$，$\bar{\alpha}$ を使って式を整理していきます。

$(1-z)(1-z^2)(1-z^3)(1-z^4)(1-z^5)(1-z^6)$
$=(1-z)(1-z^2)(1-\overline{z^4})(1-z^4)(1-\overline{z^2})(1-\bar{z})$

$=(1-z)(1-z^2)(1-z^4)(1-\bar{z})(1-\overline{z^2})(1-\overline{z^4})$

ここで

$(1-z)(1-z^2)(1-z^4)$
$=(1-z-z^2+z^3)(1-z^4)$
$=1-z^4-z+z^5-z^2+z^6+z^3-z^7$

$=1-z^4-z+\overline{z^2}-z^2+\bar{z}+\overline{z^4}-1$
$=-z-z^2-z^4+\bar{z}+\overline{z^2}+\overline{z^4}$
$=\bar{\alpha}-\alpha$

また

$(1-\bar{z})(1-\overline{z^2})(1-\overline{z^4})$
$=(1-\overline{z^2}-\bar{z}+\overline{z^3})(1-\overline{z^4})$
$=1-\overline{z^4}-\overline{z^2}+\overline{z^6}-\bar{z}+\overline{z^5}+\overline{z^3}-\overline{z^7}$
$=1-\overline{z^4}-\overline{z^2}+z-\bar{z}+z^2+z^4-1$
$=z+z^4+z^4-\bar{z}-\overline{z^2}-\overline{z^4}$
$=\alpha-\bar{\alpha}$

よって与式は

$(\bar{\alpha}-\alpha)(\alpha-\bar{\alpha})=\alpha\bar{\alpha}-\overline{\alpha^2}-\alpha^2+\alpha\bar{\alpha}$
$=2-(\alpha^2+\overline{\alpha^2})+2$
$=4-(\alpha+\overline{\alpha})^2+2\alpha\overline{\alpha}$
$=4-(-1)^2+2\cdot2$
$=7$　（答え）