【数III極限・微積分】微分とはさみうちの原理
$0$ < $t$ < $\cfrac{\pi}{2}$ のとき,曲線 $y=\cfrac{1}{\cos^2 x}\Big(0$ ≦ $x$ ≦ $\cfrac{\pi}{2}\Big)$,$x$ 軸,$y$ 軸および直線 $x=t$ で囲まれた図形を $y$ 軸のまわりに 1 回転してできる立体の体積を $V(t)$ とする。以下の問いに答えよ。(熊本大)
(問1) $0$ < $a$ < $b$ < $\cfrac{\pi}{2}$ のとき,
$\pi(b^2-a^2)\cfrac{1}{\cos^2 a}$ ≦ $V(b)-V(a)$ ≦ $\pi(b^2-a^2)\cfrac{1}{\cos^2 b}$
(問2) (問1)の不等式を用いて,$\cfrac{d}{dt}V(t)=2\pi t\cfrac{1}{\cos^2 t}$ を示せ。
(問3) $V\Big(\cfrac{\pi}{3}\Big)$ を求めよ。





不等式の証明

次のグラフを描きます。
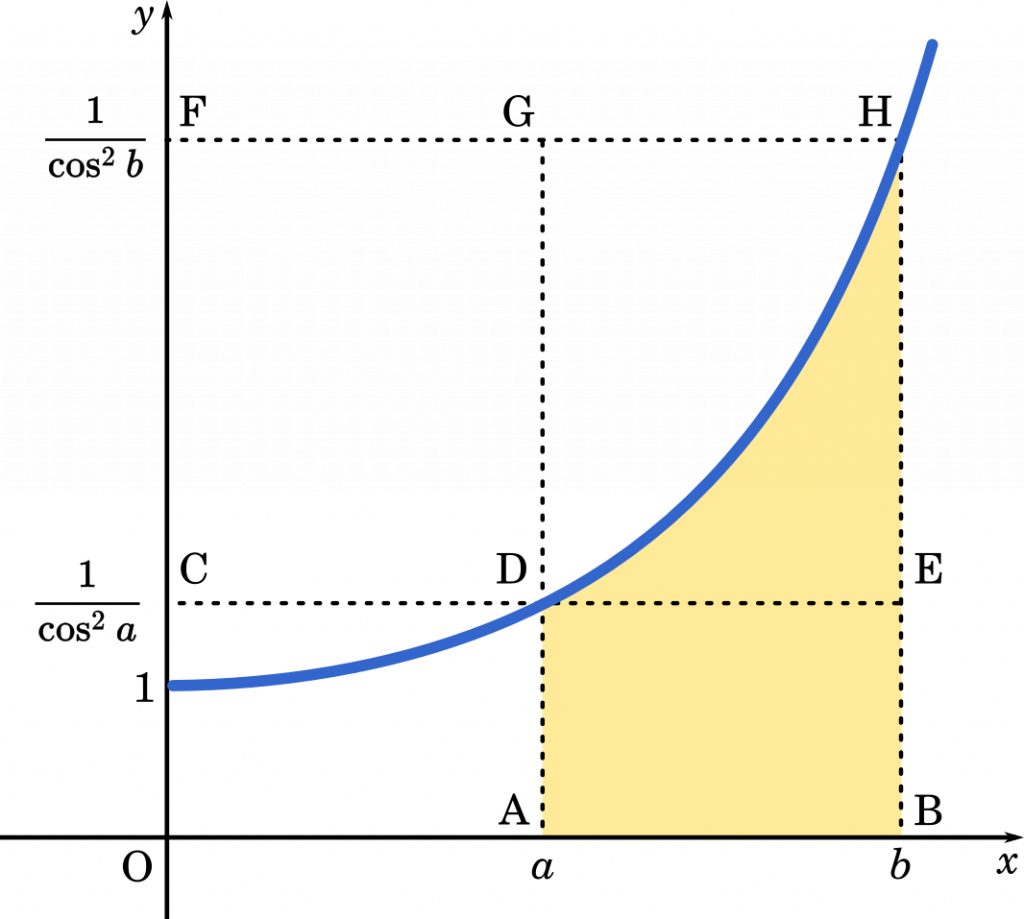
不等式の $V(b)-V(a)$ はグラフの色を塗った部分を $y$ 軸のまわりに 1 回転してできる立体の体積です。

不等式をつくるためには,色を塗った部分の面積よりも小さな部分と大きな部分を考えると良いでしょう。そうすると
四角形 ABED < 色を塗った部分 < 四角形 ABHG
という関係が見えてきます。
四角形 ABED を $y$ 軸のまわりに 1 回転すると円柱の真ん中に穴があいた立体ができます。
この体積は,半径 $b$ の円柱から半径 $a$ の円柱をひけば求められそうです。高さは $\cfrac{1}{\cos^2 a}$ です。

四角形ABEDを $y$ 軸のまわりに 1 回転してできる立体の体積は
$\pi b^2\cfrac{1}{\cos^2 a}-\pi a^2\cfrac{1}{\cos^2 a}$
$=\pi(b^2-a^2)\cfrac{1}{\cos^2 a}$


また,四角形 ABHG を $y$ 軸のまわりに 1 回転してできる立体の体積は
$\pi b^2\cfrac{1}{\cos^2 b}-\pi a^2\cfrac{1}{\cos^2 b}$
$=\pi(b^2-a^2)\cfrac{1}{\cos^2 b}$
したがって
$\pi(b^2-a^2)\cfrac{1}{\cos^2 a}$ ≦ $V(b)-V(a)$ ≦ $\pi(b^2-a^2)\cfrac{1}{\cos^2 b}$ (証明終わり)
はさみうちの原理に持ち込む
次に $\cfrac{d}{dt}V(t)=2\pi t\cfrac{1}{\cos^2 t}$ を考えます。
$\cfrac{d}{dt}V(t)$ というのは体積の式を $t$ で微分するということです。


$a=t$,$b=t+h$ とすると
$\displaystyle\cfrac{d}{dt}V(t)=\lim_{h\rightarrow0}\cfrac{V(t+h)-V(t)}{h}$
と表すことができる。(問1)の不等式を $h$ で割ると
$\pi(b^2-a^2)\cfrac{1}{\cos^2 a}$ ≦ $V(b)-V(a)$ ≦ $\pi(b^2-a^2)\cfrac{1}{\cos^2 b}$
$\pi(b^2-a^2)\cfrac{1}{h\cos^2 a}$ ≦ $\cfrac{V(b)-V(a)}{h}$ ≦ $\pi(b^2-a^2)\cfrac{1}{h\cos^2 b}$
$a=t$,$b=t+h$ を代入して
$\cfrac{\pi\{(t+h)^2-t^2\}}{h\cos^2 t}$ ≦ $\cfrac{V(t+h)-V(t)}{h}$ ≦ $\cfrac{\pi\{(t+h)^2-t^2\}}{h\cos^2 (t+h)}$

ここで
$\displaystyle\lim_{h\rightarrow0}\cfrac{\pi\{(t+h)^2-t^2\}}{h\cos^2 t}$
$=\displaystyle\lim_{h\rightarrow0}\cfrac{\pi(t^2+2ht+h^2-t^2)}{h\cos^2 t}$
$=\displaystyle\lim_{h\rightarrow0}\cfrac{\pi(2ht+h^2)}{h\cos^2 t}$
$=\displaystyle\lim_{h\rightarrow0}\cfrac{\pi(2t+h)}{\cos^2 t}$
$=\cfrac{2\pi t}{\cos^2 t}$
また
$\displaystyle\lim_{h\rightarrow0}\cfrac{\pi\{(t+h)^2-t^2\}}{h\cos^2 (t+h)}$
$=\displaystyle\lim_{h\rightarrow0}\cfrac{\pi(t^2+2ht+h^2-t^2)}{h\cos^2 (t+h)}$
$=\displaystyle\lim_{h\rightarrow0}\cfrac{\pi(2ht+h^2)}{h\cos^2 (t+h)}$
$=\displaystyle\lim_{h\rightarrow0}\cfrac{\pi(2t+h)}{\cos^2 (t+h)}$
$=\cfrac{2\pi t}{\cos^2 t}$
したがって,はさみうちの原理より
$\cfrac{d}{dt}V(t)=2\pi t\cfrac{1}{\cos^2 t}$ (証明終わり)
部分積分を用いて体積を求める
体積を微分した式が求められたので,これを積分すればもとの体積の式が作れそうです。
$\cfrac{d}{dt}V(t)=2\pi t\cfrac{1}{\cos^2 t}$ より
$\displaystyle V\Big(\cfrac{\pi}{3}\Big)=\int_0^{\small{\frac{\pi}{3}}} 2\pi t\cfrac{1}{\cos^2 t} \space dt$
式はかけ算の形になっているので,部分積分を使って積分していきます。
公式 $(\tan x)’=\cfrac{1}{\cos^2 t}$ より
$\displaystyle=\int_0^{\small{\frac{\pi}{3}}} 2\pi t(\tan t)’ \space dt$
$\displaystyle=\Big[2\pi t\tan t\Big]_0^{\small{\frac{\pi}{3}}}-\int_0^{\small{\frac{\pi}{3}}} 2\pi\tan t \space dt$
$\displaystyle=2\pi\Big[t\tan t\Big]_0^{\small{\frac{\pi}{3}}}-2\pi\int_0^{\small{\frac{\pi}{3}}} \cfrac{\sin t}{\cos t} \space dt$
ここで公式 $(\log x)’=\cfrac{1}{x}$ と,合成関数の微分より
$\{\log|\cos x|\}’=\cfrac{1}{\cos x}\cdot(\cos x)’$
$=-\cfrac{\sin x}{\cos x}$
となる。

よって与式は
$\displaystyle=\Big[2\pi t\tan t\Big]_0^{\small{\frac{\pi}{3}}}+2\pi\Big[\log\cos t \space\Big]_0^{\small{\frac{\pi}{3}}}$
$=2\pi\cdot\cfrac{\pi}{3}\cdot\tan\cfrac{\pi}{3}+2\pi\log\cos\cfrac{\pi}{3}-2\pi\log\cos0$
$=2\pi\cdot\cfrac{\pi}{3}\cdot\sqrt{3}+2\pi\log\cfrac{1}{2}-2\pi\log 1$
$\log 1=0$ に注意して
$=\cfrac{2\sqrt{3}}{3}\pi^2+2\pi(\log 1-\log 2)$
$=\cfrac{2\sqrt{3}}{3}\pi^2-2\pi\log 2$
$=2\pi\Big(\cfrac{\sqrt{3}}{3}\pi-\log 2\Big)$ (答え)
SNSでシェア