【数Ⅲ微分】平均値の定理を利用して式の大小関係を判別する

正の実数 $a,b,p$ に対して、$A=(a+b)^p$ と $B=2^{p-1}(a^p+b^p)$ の大小関係を調べよ。（東京工業大）

---

$y=x^p$ のグラフを考えて式をまとめる

式の大小関係を調べるには引き算をすれば分かります。$B-A$ が正の値なら $A<B$、負の値なら $A>B$ です。そこで、$B-A$ を求めてみましょう。

$\displaystyle B-A=2^{p-1}(a^p+b^p)-(a+b)^p$

文字の値に範囲が定められていない場合、式がプラスになるかマイナスになるかを判断できる形はある程度決まっています。例えば、正の数×正の数ならプラスになるし、負の数×負の数もプラスです。また、式が正の数＋正の数ならばプラスであると判断できますが、正の数ー正の数だと値の大きさによってプラスになるときもあればマイナスになるときもあります。この考えから言えば、正の数×正の数＋正の数はプラスですし、正の数×正の数ー正の数は判断不能です。

こうやって様々な場合を考えてみると、とにかく式の中に引き算がない形に持っていけば何とかなりそうだ、という結論になります。そこで今回は一番シンプルな形の正の数×正の数に変形していくことをイメージして話を進めていきしょう。

$\displaystyle =2^{p-1}\left\{a^p+b^p-\frac{(a+b)^p}{2^{p-1}}\right\}$

こうすることで、$2^{p-1}$ をいったん外に追い出します。$2^{p-1}$ は $p$ にどんな値が入ろうとも必ず正の値になるので、あとは $\displaystyle \left\{a^p+b^p-\frac{(a+b)^p}{2^{p-1}}\right\}$ の部分が正になるか負になるかを考えればよいことになります。

とは言え、ここから式の正負を判断することはできません。そこで、式をよく見てみましょう。そうすると式の中に $x^p$ のような形が共通していることが分かります。

$y=x^p$ のグラフはイメージとしてはこのような感じです。

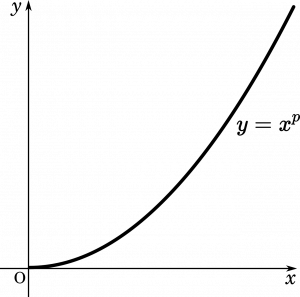
$y=x^2$ や $y=x^3$ のグラフを考えてみれば、$y=x^p$ は $p$ の値が何であろうと、$x$ が正の部分においてはいずれも上のような形のグラフになるはずです。

ここで、$a^p$ は言い換えれば $x$ 座標が $a$ のときの $y$ 座標を表しているということです。$b^p$ も同様で、図で表すとこのようになります。

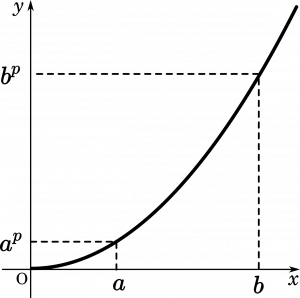
こうすると、$y$ 座標の大小関係から式の正負を考えることができそうです。

とは言え、このままでは何もできないので式をもう少し整理します。基本的には $y$ 座標の大小で考えていく方針なので、$x^p$ の形でまとめていきます。

$\displaystyle =2^{p-1}\left\{a^p+b^p-\frac{2(a+b)^p}{2^p}\right\}\\\displaystyle =2^{p-1}\left\{a^p+b^p-2\left(\frac{a+b}{2}\right)^p\right\}$

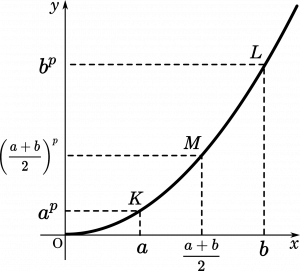
式から考えると、$y$ 座標において $K$ と $L$ を足したものから $M$ の $2$ 倍を引いたらプラスになるかマイナスになるか、という問題になります。しかし、その考えでは判断は難しそうです。

傾きの大きさの違いから大小関係を考える

この考えに基づいて、さらに式を変形してみましょう。

$\displaystyle =2^{p-1}\left\{a^p-\left(\frac{a+b}{2}\right)^p+b^p-\left(\frac{a+b}{2}\right)^p\right\}\\\displaystyle=2^{p-1}\left[\left\{b^p-\left(\frac{a+b}{2}\right)^p\right\}-\left\{\left(\frac{a+b}{2}\right)^p-a^p\right\}\right]$

この式は $M-L$ 間の $y$ の変化量から $K-M$ 間の $y$ の変化量を引いている、ということです。

さらに考えを進めます。$y$ の変化量は言いかえれば直線の傾きの大きさとも言えます。今回の式では $K-M$ 間と $M-L$ 間の $x$ の変化量は同じなので、$y$ の変化量の大小は、傾きの大きさの大小に置きかえても大丈夫です。

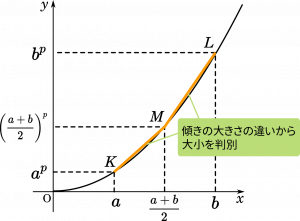
そこで、一度傾きを考えてみましょう。

$K-M$ 間の傾きは

$\displaystyle\frac{\left(\frac{a+b}{2}\right)^p-a^p}{\frac{a+b}{2}-a}=\frac{\left(\frac{a+b}{2}\right)^p-a^p}{\frac{a+b-2a}{2}}\\\displaystyle=\frac{\left(\frac{a+b}{2}\right)^p-a^p}{\frac{b-a}{2}}$

また、$M-L$ 間も同様に

$\displaystyle\frac{b^p-\left(\frac{a+b}{2}\right)^p}{\frac{b-a}{2}}$

平均値の定理を用いて傾きを別な方法で表す

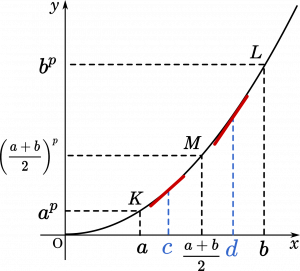
平均値の定理を用いると、$K-M$ の傾き＝$c$ における接線の傾き、となる $c$ が存在するはずです。同様に $d$ も存在します。

$y=x^p$ における接線の傾きは

$y’=px^{p-1}$

よって、$x=c$ における接線の傾きは $pc^{p-1}$ となる。

$K-M$ 間の傾きと $c$ における接線の傾きは一致するので

$\displaystyle\frac{\left(\frac{a+b}{2}\right)^p-a^p}{\frac{b-a}{2}}=pc^{p-1}\\\displaystyle\left(\frac{a+b}{2}\right)^p-a^p=\frac{b-a}{2}pc^{p-1}$

同様に、$x=d$ における接線の傾きは $pd^{p-1}$ となり、$M-L$ 間の傾きと $d$ における接線の傾きは一致するので

$\displaystyle b^p-\left(\frac{a+b}{2}\right)^p=\frac{b-a}{2}pd^{p-1}$

これを先ほど求めた

$\displaystyle B-A=2^{p-1}\left[\left\{b^p-\left(\frac{a+b}{2}\right)^p\right\}-\left\{\left(\frac{a+b}{2}\right)^p-a^p\right\}\right]$

に代入すると

$\displaystyle B-A=2^{p-1}\left(\frac{b-a}{2}pd^{p-1}-\frac{b-a}{2}pc^{p-1}\right)$
$\displaystyle =2^{p-1}\cdot\frac{b-a}{2}\cdot p(d^{p-1}-c^{p-1})$

ここで、$2^{p-1}$ と $\displaystyle\frac{b-a}{2}$ は常に正であることが分かる。

次に、$d^{p-1}-c^{p-1}$ は $0<p<1$ のとき $d^{p-1}<c^{p-1}$ となるので、負の値となる。また、$p>1$ のとき正の値となる。そして、$p=1$ のときは、$d^{1-1}-c^{1-1}=1-1=0$ となる。

さらに、$a=b$ のとき式の値は $0$ となる。

以上をまとめると

$a\ne b$ のとき、

$0<p<1$ なら $A>B$.

$p=1$ なら $A=B$.

$p>1$ なら $A<B$.

また $a=b$ のとき、$A=B$.　（答え）

今回のポイントは多項式で表す傾きを平均値の定理を用いて単項式に変換するところです。テクニックとして使えるように復習してみましょう。