【数Ⅱ図形と方程式】2つの円の交点を通る図形


問 2つの円 $x^2+y^2-10=0,\enspace x^2+y^2-12x-6y+20=0 $がある。
(1) 2つの円の共有点を通る直線の方程式を求めよ。
(2) 2つの円の共有点の座標を求めよ。
(3) 2つの円の共有点と点(0,4)を通る円の方程式を求めよ。
2つの円の共有点を通る直線の方程式
(1)から考えていきましょう。2つの式を連立して整理していきます。
$\begin{cases}\displaystyle x^2+y^2-10=0\cdots\text{①}\\x^2+y^2-12x-6y+20=0\cdots\text{②}\end{cases}$
①-②より
$12x+6y-30=0$
したがって
$y=-2x+5$ (答え)
[te]この直線 $y=-2x+5$ は2つ円の共有点を通る直線の式になるよ。
なぜ連立方程式を解くと交点が出るのか
その前に一度中学校に戻って、なぜ連立方程式を解くと交点の座標が求められるのか?を考えてみましょう。
$\begin{cases}\displaystyle 2x+y=5\enspace\cdots\text{①}\\3x+2y=8\cdots\text{②}\end{cases}$


①×2-② で $x=2$、①に代入して $y=1$ (答え)

ここからが大事なポイントです。式どうしを引き算してもよい理由は恒等式の性質があるからです。
$a=b,\enspace c=d$なら、$a-c=b-d$
ここで、もし2つの式の $x, y$ に別々な値が入るとしたらどうなるでしょう?
$\begin{cases}\displaystyle 2x+y=5\enspace\cdots\text{①}\\3X+2Y=8\cdots\text{②}\end{cases}$
同じように ①×2ー② をすると
$4x-3X+2y-2Y=2$
となります。
[st]ん?$4x-3X=x$ ってしたらダメなの?[/st] [te]$x$ と $X$ は別な文字だから引いたらダメだよ。
つまりこういうことです。連立方程式で2つの式を合体させたときに $x$ どうしで引き算ができるのは、2つの式の $x$ には同じ値が入るという前提があるからです。
図で見ると、こういう感じです。

上と下の $x, \enspace y$どうしが同じ大きさだと仮定するから、引き算をして $y$ を消去できるのです。
連立で直線の式ができるのはたまたま
もう一度、先ほどの問題に戻りましょう。
$\begin{cases}\displaystyle x^2+y^2-10=0\cdots\text{①}\\x^2+y^2-12x-6y+20=0\cdots\text{②}\end{cases}$
ここで ① と ② の$x,\enspace y$にそれぞれ同じ値が入ると仮定して①-②の計算をします。2つの式は円を表しているので、そこに入る値は2つの円の共有点の座標であるはずです(上で説明した通り、2つの式の $x,y$ に同じ数が入らないと連立方程式が成り立たない)。
$12x+6y-30=0\\y=-2x+5$


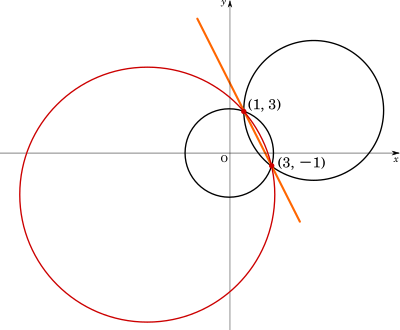
つまり、$y=-2x+5$ は共有点 $(1,3),(3,-1)$ を通る直線の式ということになるのです。




逆に言えば、直線にならないこともあります。例えば、2つの円が
$\displaystyle 3x^2+2y^2-4=0\cdots\text{①}$
$2x^2+4y^2+2x+5y-10=0\cdots\text{②}$
の場合、連立して①×2ー②を計算すると
$\displaystyle y=\frac{4}{5}x^2-\frac{2}{5}x+\frac{2}{5}$
となり、放物線になります。ちなみに、この2つの円は楕円です。
2つの円の共有点の座標を求める
問題(2)に進みましょう。2つの円は
$\begin{cases}\displaystyle x^2+y^2-10=0\cdots\text{①}\\x^2+y^2-12x-6y+20=0\cdots\text{②}\end{cases}$
(1)で出した$y=-2x+5$を①に代入します。
$x^2+(-2x+5)^2-10=0$
$x^2-4x+3=0$
$(x-1)(x-3)=0$
$x=1,\enspace 3$
これを$y=-2x+5$に代入して
$x=1$ のとき $y=3$
$x=3$ のとき $y=-1$
よって、共有点の座標は$(1,3),(3,-1)$ (答え)
2つの円と点(0,4)を通る円の方程式
(3)に進みます。
$k$ を定数として
$k(x^2+y^2-10)+(x^2+y^2-12x-6y+20)=0\enspace\cdots\text③$
とします。




もし、$k=-1$ とすると、$x^2,\enspace y^2$ の項が消えるので直線の式になります。(1)でやったことと同じですね。しかし今回は、円の方程式にするので、kには-1以外の値を入れて$x^2,\enspace y^2$の項が消えないようにしなければなりません。
kの値によっていろいろな円の方程式ができます。しかし、それらは全て2つの円の共有点を通る円になっているのです。

そこでもう一つの条件、点(0,4)を③にそれぞれ代入してみます。
$k(0+16-10)+(0+16-0-24+20)=0$
$k=-2$

これを③に戻すと
$-2(x^2+y^2-10)+(x^2+y^2-12x-6y+20)=0$
$x^2+y^2+12x+6y-40=0$
平方完成に持ち込みます。
$(x+6)^2-36+(y+3)^2-9-40=0$
$(x+6)^2+(y+3)^2=85$ (答え)
2つの円の共有点の問題は連立方程式の復習から
中学の時に連立方程式の解き方を習って、何となくやり方だけ覚えて問題を解いていた人も多いと思います。この問題を理解するためには、連立方程式がなぜ成り立つのか?を正しく理解する必要があります。もう一度振り返って復習してみましょう。
SNSでシェア