【数II微分】定数分離の実践問題(北海道大2019文系第4問)

実数 $a,b,c$ に対し，関数 $f(x)=x^3-3ax^2+bx+c$ を考える。1 次関数 $g(x)$ があり，$f(x)$ とその導関数 $f'(x)$ は，すべての $x$ に対し等式 $f(x)=f'(x)g(x)-6x$ を満たしているとする。

(1) $b$ と $c$ を $a$ で表せ。

(2) 3 次方程式 $f(x)=0$ が異なる 3 つの実数解をもつように，$a$ の値の範囲を定めよ。

(北海道大2019)

係数を比較する

(1)から始めます。

$f(x)=x^3-3ax^2+bx+c$ ・・・①より
$f'(x)=3x^2-6ax+b$
$g(x)=px+q$ とおくと
$f(x)=(3x^2-6ax+b)(px+q)-6x$
$=3px^3+3qx^2-6apx^2-6aqx+bpx+bq-6x$
$=3px^3+(3q-6ap)x^2+(-6aq+bp-6)x+bg$ ・・・②

①と②の係数を比べると
$1=3p$ ・・・③
$-3a=3q-6ap$ ・・・④
$b=-6aq+bp-6$ ・・・⑤
$c=bq$ ・・・⑥

③より $p=\cfrac{1}{3}$
④に代入して
$-3a=3q-2a$
$3q=-a$
$q=-\cfrac{a}{3}$
⑤に代入して
$b=-6a\Big(-\cfrac{a}{3}\Big)+\cfrac{1}{3}b-6$
$\cfrac{2}{3}b=2a^2-6$
$b=3a^2-9$
⑥に代入して
$c=(3a^2-9)\Big(-\cfrac{a}{3}\Big)$
$=-a^3+3a$

したがって
$(b,c)=(3a^2-9,-a^3+3a)$ (答え)

定数分離

(2)に進みます。

(1)より
$f(x)=x^3-3ax^2+(3a^2-9)x-a^3+3a=0$

$x^3-3ax^2+(3a^2-9)x=a^3-3a$

たとえば，$x^2-5x+6=0$ の解を求るとき，$(x-2)(x-3)=0$，$x=2,3$ とします。このとき，$2,3$ は関数の値が 0 になる，つまり $y=0$ になる点のことです。解は2つだから，$y=0$ になる点は 2 つ存在しています。

ここでは，$y=0$ ではなく，$y=a^3-3a$ になる点を考えます。これが定数分離です。

$h(x)=x^3-3ax^2+(3a^2-9)x$ として
$h'(x)=3x^2-6ax+3a^2-9$
$3x^2-6ax+3a^2-9=0$ とすると
$x^2-2ax+a^2-3=0$
$x=a\pm\sqrt{a^2-a^2+3}$
$=a\pm\sqrt{3}$

増減表は

$\def\arraystretch{1.5}\begin{array}{c|||c|c|c|c|c|}x&\cdots&a-\sqrt{3}&\cdots&a+\sqrt{3}&\cdots\\\hline h'(x)&+&0&-&0&+\\\hline h(x)&\nearrow&&\searrow&&\nearrow\end{array}$

$h(a-\sqrt{3})=(a-\sqrt{3})\{(a-\sqrt{3})^2-3a(a-\sqrt{3})+3a^2-9\}$
$=(a-\sqrt{3})(a^2-2\sqrt{3}a+3-3a^2+3\sqrt{3}a+3a^2-9)$
$=(a-\sqrt{3})(a^2+\sqrt{3}a-6)$
$=a^3+\sqrt{3}a^2-6a-\sqrt{3}a^2-3a+6\sqrt{3}$
$=a^3-9a+6\sqrt{3}$

$h(a+\sqrt{3})=(a+\sqrt{3})\{(a+\sqrt{3})^2-3a(a+\sqrt{3})+3a^2-9\}$
$=(a+\sqrt{3})(a^2+2\sqrt{3}a+3-3a^2-3\sqrt{3}a+3a^2-9)$
$=(a+\sqrt{3})(a^2-\sqrt{3}a-6)$
$=a^3-\sqrt{3}a^2-6a+\sqrt{3}a^2-3a-6\sqrt{3}$
$=a^3-9a-6\sqrt{3}$

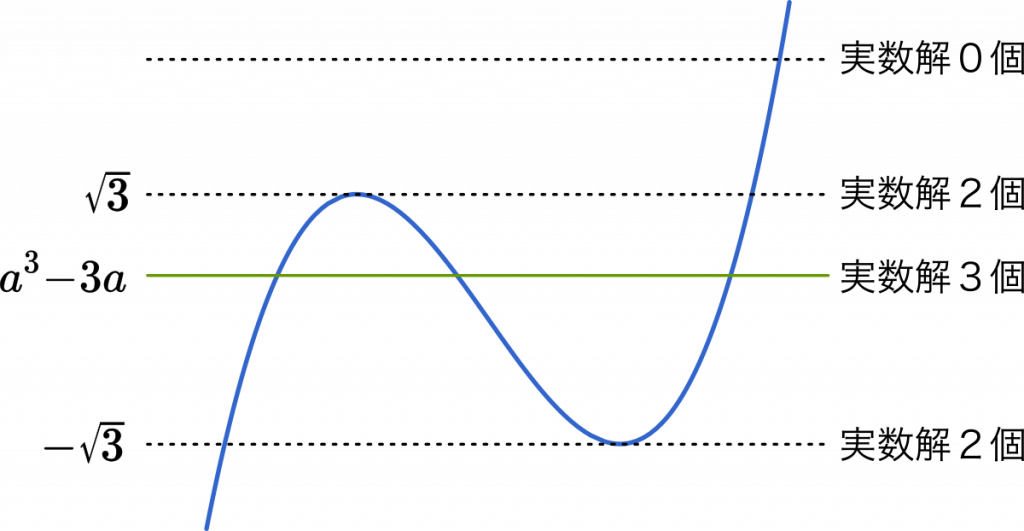
よって
$a^3-9a-6\sqrt{3}<a^3-3a<a^3-9a+6\sqrt{3}$
が成り立つ。不等式を分解して
$a^3-9a-6\sqrt{3}<a^3-3a$
$-6a<6\sqrt{3}$
$a>-\sqrt{3}$
また
$a^3-3a<a^3-9a+6\sqrt{3}$
$6a<6\sqrt{3}$
$a<\sqrt{3}$

したがって
$-\sqrt{3}<a<\sqrt{3}$ (答え)