【数IIB】相加相乗平均を使って最大値を求める　分数式での使い方(千葉大2010第9問)

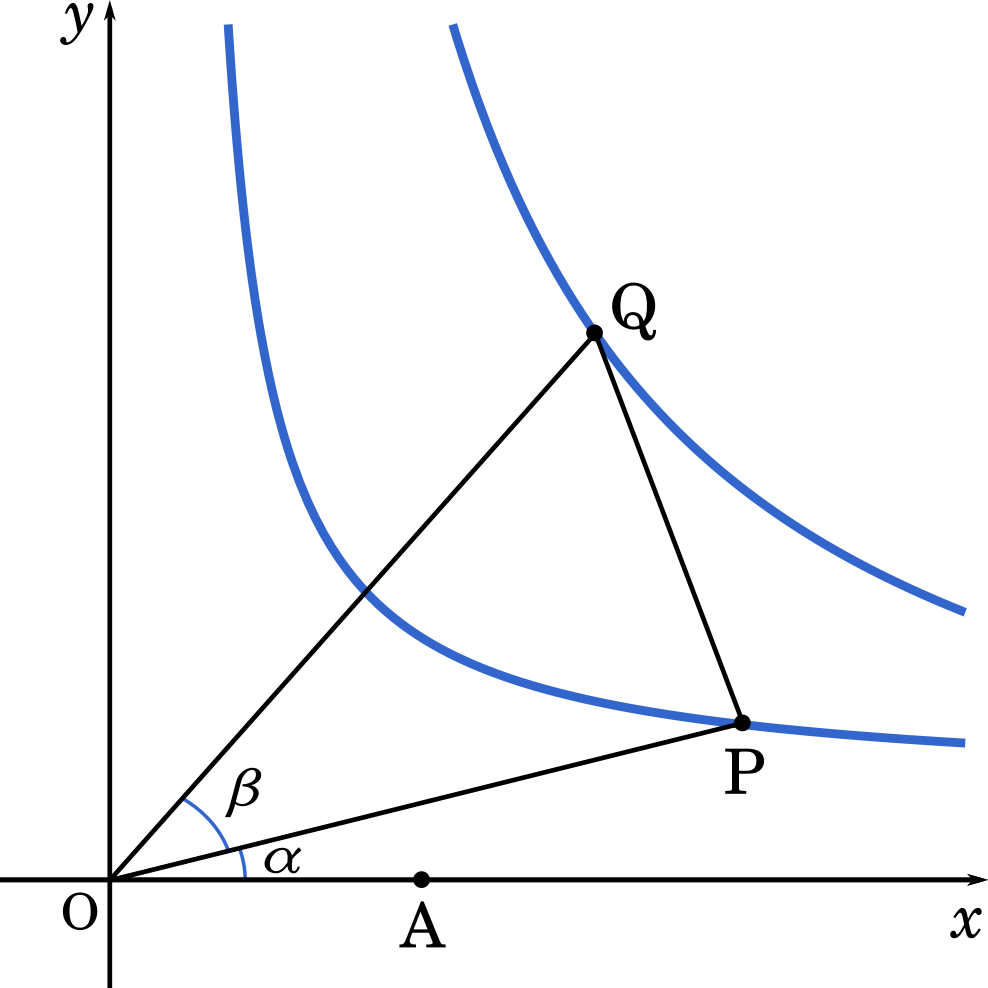
$a$ を 1 より大きい実数とし，座標平面上に，点 O(0,0)，A(1,0) をとる。
曲線 $y=\cfrac{1}{x}$ 上の点 P $\Big(p,\cfrac{1}{p}\Big)$ と，曲線 $y=\cfrac{a}{x}$ 上の点 Q $\Big(q,\cfrac{a}{q}\Big)$ が,3条件

(1) $p$ ＞ 0，$q$ ＞ 0
(2) ∠AOP ＜ ∠AOQ
(3) △OPQ の面積は 3 に等しい

をみたしながら動くとき，$\tan$ ∠POQ の最大値が $\cfrac{3}{4}$ となるような $a$ の値を求めよ。(千葉大2010)

ここでは相加相乗平均の使い方を学習します。

tan の加法定理を使う

∠AOP = $\alpha$，∠AOQ = $\beta$ とすると
$\tan(\beta-\alpha)=\cfrac{\tan\beta-\tan\alpha}{1+\tan\alpha\tan\beta}$
となります。
ここで，$\tan$ を求めると
$\tan\alpha=\cfrac{\space\cfrac{1}{p}\space}{p}=\cfrac{\space\cfrac{1}{p}\times p\space}{p\times p}=\cfrac{1}{p^2}$

また
$\tan\beta=\cfrac{\cfrac{a}{q}}{q}=\cfrac{a}{q^2}$
よって
$\tan(\beta-\alpha)=\cfrac{\cfrac{a}{q^2}-\cfrac{1}{p^2}}{1+\cfrac{1}{p^2}\cdot\cfrac{a}{q^2}}$
$=\cfrac{\Big(\cfrac{a}{q^2}-\cfrac{1}{p^2}\Big)\times p^2q^2}{\Big(1+\cfrac{1}{p^2}\cdot\cfrac{a}{q^2}\Big)\times p^2q^2}$
$=\cfrac{ap^2-q^2}{p^2q^2+a}$ ・・・①

三角形の面積

問題文より，これの最大値が $\cfrac{3}{4}$ になる場合を考えることになります。とは言え，このままではどうしようもないので面積が 3 であるという条件について式を立ててみます。

ここで公式を思い出しましょう。

△OPQ = $\cfrac{1}{2}\Big|p\cdot\cfrac{a}{q}-\cfrac{1}{p}\cdot q\Big|$
$\cfrac{1}{2}\Big|\cfrac{ap^2-q^2}{pq}\Big|=3$

$\cfrac{|ap^2-q^2|}{|pq|}=6$
$p$ ＞ 0，$q$ ＞ 0 だから $|pq|=pq$
$|ap^2-q^2|=6pq$

これを①に代入します。①が $\cfrac{3}{4}$ だとしたら，それは正の値です。①の分母は正の値だから分子も正の値です。よって絶対値の記号をはずしても構いません。

$\tan(\beta-\alpha)=\cfrac{6pq}{p^2q^2+a}$

相加相乗平均の用い方

ここから式の最大値が $\cfrac{3}{4}$ である，という条件を考えます。

相加相乗平均より
$p^2q^2+a$ ≧ $2\sqrt{ap^2q^2}$
$p^2q^2+a$ ≧ $2pq\sqrt{a}$
等号成立は $p^2q^2=a$ つまり $pq=\sqrt{a}$ のとき。
よって
$\cfrac{6pq}{p^2q^2+a}=\cfrac{6\sqrt{a}}{a+a}=\cfrac{3\sqrt{a}}{a}$
最大値は $\cfrac{3}{4}$ だから
$\cfrac{3\sqrt{a}}{a}=\cfrac{3}{4}$
$\cfrac{1}{\sqrt{a}}=\cfrac{1}{4}$
$a=16$ (答え)