【数IIB三角関数】一つのsinに値に当てはまるθが1個のときと2個のときを判別する(北海道大2020文系第2問)

関数

$f(\theta)=\cfrac{1}{\sqrt{2}}\sin2\theta-\sin\theta+\cos\theta\enspace(0\leqq\theta\leqq\pi)$
を考える。(北海道大2020)

(1) $t=\sin\theta-\cos\theta$ とおく。$f(\theta)$ を $t$ の式で表せ。

(2) $f(\theta)$ の最大値と最小値，およびそのときの $\theta$ の値を求めよ。

(3) $a$ を実数の定数とする。$f(\theta)=a$ となる $\theta$ がちょうど 2 個であるような $a$ の範囲を求めよ。

2倍角の公式を使う

(1)から始めます。

まず，与式の中に $\sin2\theta$ があります。これは 2 倍角です。

よって，$t$ の式を変形して，$2\sin\theta\cos\theta$ の形を作る必要があります。

式を 2 乗してみましょう。

$t=\sin\theta-\cos\theta$
$t^2=\sin^2\theta-2\sin\theta\cos\theta+\cos^2\theta$

$\sin^2\theta+\cos^2\theta=1$ より

$=1-2\sin\theta\cos\theta$
$=1-\sin2\theta$
$\sin2\theta=1-t^2$

よって

$f(\theta)=\cfrac{1}{\sqrt{2}}\sin2\theta-(\sin\theta-\cos\theta)$
$=\cfrac{1}{\sqrt{2}}(1-t^2)-t$
$=-\cfrac{1}{\sqrt{2}}t^2-t+\cfrac{1}{\sqrt{2}}$ (答え)

平方完成して最大・最小を求める

(2)に進みます。

$f(\theta)$ は $t$ の2次関数になったので，平方完成すれば，最大・最小が求められそうです。

$f(\theta)=-\cfrac{1}{\sqrt{2}}t^2-t+\cfrac{1}{\sqrt{2}}$
$=-\cfrac{1}{\sqrt{2}}(t^2+\sqrt{2}t)+\cfrac{1}{\sqrt{2}}$
$=-\cfrac{1}{\sqrt{2}}\Big(t+\cfrac{\sqrt{2}}{2}\Big)^2+\cfrac{1}{2\sqrt{2}}+\cfrac{1}{\sqrt{2}}$
$=-\cfrac{1}{\sqrt{2}}\Big(t+\cfrac{\sqrt{2}}{2}\Big)^2+\cfrac{3}{2\sqrt{2}}$
$=-\cfrac{1}{\sqrt{2}}\Big(t+\cfrac{\sqrt{2}}{2}\Big)^2+\cfrac{3\sqrt{2}}{4}$

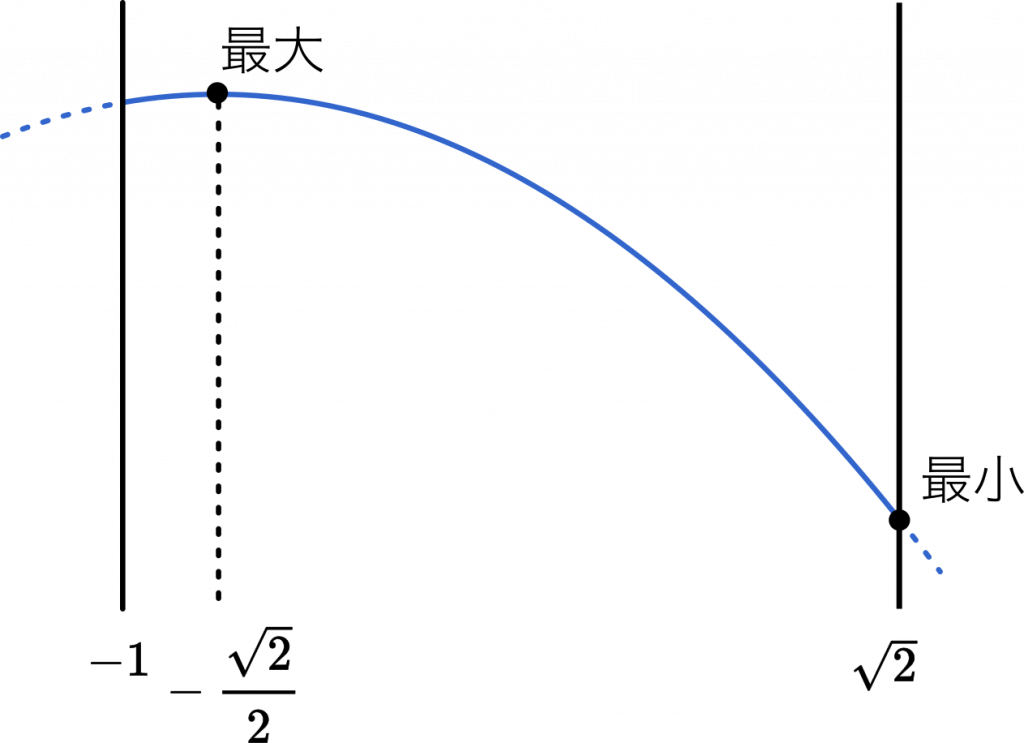
よって，$t=-\cfrac{\sqrt{2}}{2}$ で最大値をとる。

$t=-\cfrac{\sqrt{2}}{2}$ とすると

$f(\theta)=-\cfrac{1}{\sqrt{2}}\Big(-\cfrac{\sqrt{2}}{2}+\cfrac{\sqrt{2}}{2}\Big)^2+\cfrac{3\sqrt{2}}{4}$
$=\cfrac{3\sqrt{2}}{4}$

また，このときの $\theta$ の値を求めます。

式が $t=\sin\theta-\cos\theta$ のままでは，$\theta$ の値が分からないので，三角関数の合成を用いると良いでしょう。

三角関数の合成より

$t=\sqrt{2}\sin\Big(\theta-\cfrac{\pi}{4}\Big)$

$t=-\cfrac{\sqrt{2}}{2}$ として，$\theta$ を求めます。

$\sqrt{2}\sin\Big(\theta-\cfrac{\pi}{4}\Big)=-\cfrac{\sqrt{2}}{2}$
$\sin\Big(\theta-\cfrac{\pi}{4}\Big)=-\cfrac{1}{2}$

$0\leqq\theta\leqq\pi$ より

$\theta-\cfrac{\pi}{4}=-\cfrac{\pi}{6}$
$\theta=\cfrac{\pi}{6}+\cfrac{\pi}{4}$
$=\cfrac{\pi}{12}$

また，上の図より，最小値は $t=\sqrt{2}$ のときです。

$f(\theta)=-\cfrac{1}{\sqrt{2}}\Big(\sqrt{2}+\cfrac{\sqrt{2}}{2}\Big)^2+\cfrac{3\sqrt{2}}{4}$
$=-\cfrac{1}{\sqrt{2}}\Big(\cfrac{3\sqrt{2}}{2}\Big)^2+\cfrac{3\sqrt{2}}{4}$
$=-\cfrac{\sqrt{2}}{2}\cdot\cfrac{18}{4}+\cfrac{3\sqrt{2}}{4}$
$=\cfrac{-9\sqrt{2}+3\sqrt{2}}{4}$
$=-\cfrac{3\sqrt{2}}{2}$

$t=\sqrt{2}$ として $\theta$ の値を求めます。

$\sqrt{2}=\sqrt{2}\sin\Big(\theta-\cfrac{\pi}{4}\Big)$
$\sin\Big(\theta-\cfrac{\pi}{4}\Big)=1$
$\theta-\cfrac{\pi}{4}=\cfrac{\pi}{2}$
$\theta=\cfrac{3}{4}\pi$

したがって

$\theta=\cfrac{\pi}{12}$ のとき，最大値 $\cfrac{3\sqrt{2}}{4}$
$\theta=\sqrt{2}$ のとき，最小値 $\cfrac{3}{4}\pi$ (答え)

1 個の t の値に当てはまる θ の個数を考える

(3)に進みます。

横軸を $t$ としてグラフを描くと，このようになります。

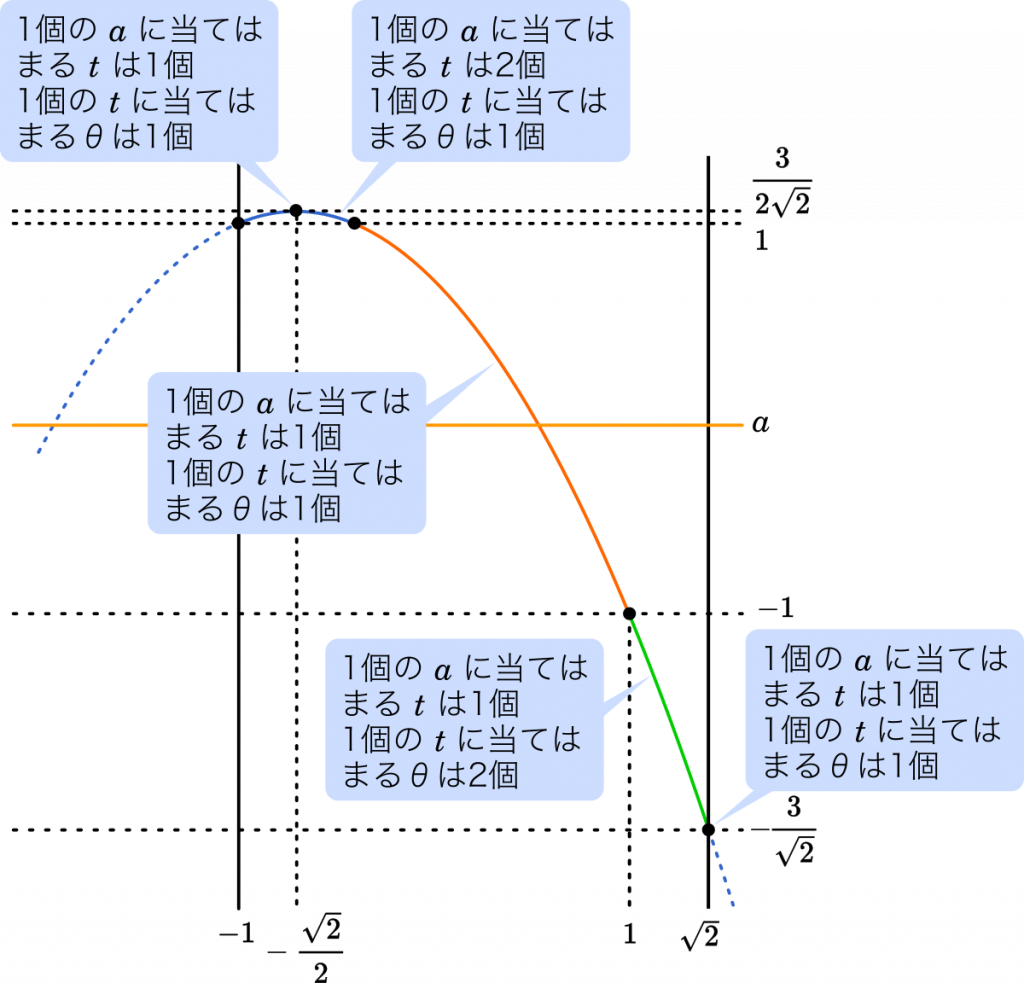
$a$ を縦方向に平行移動していくと，$a$ の値によって，あてはまる $t$ の値が，1個，2個の場合が出てくるのが分かります。

しかし，今回問われているのは，$t$ ではなく $\theta$ です。
注意しなければならないことは，1 つの $t$ の値にあてはまる $\theta$ は 1 つとは限らないことです。

$t=\sqrt{2}\sin\Big(\theta-\cfrac{\pi}{4}\Big)$ について
$0\leqq\theta\leqq\pi$ より

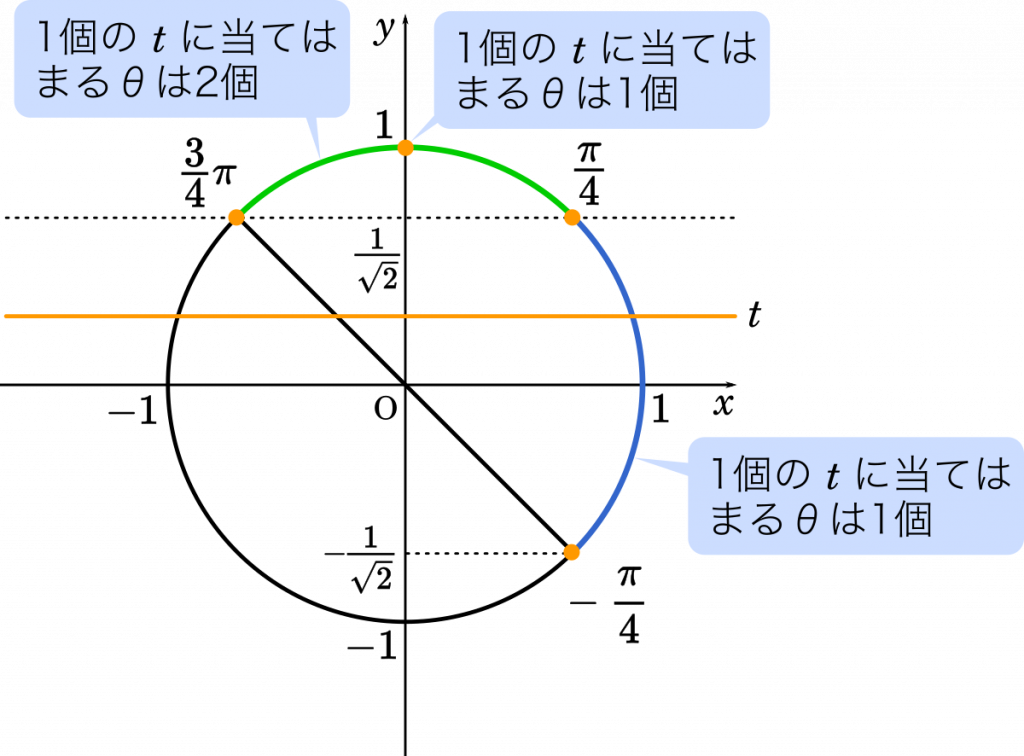
$-\cfrac{\pi}{4}\leqq\theta\leqq\cfrac{\pi}{4}$ のとき，1 個の $t$ に対して，当てはまる $\theta$ は 1 個。

$\cfrac{\pi}{4}\leqq\theta\leqq\cfrac{3}{4}\pi$ のとき，1 個の $t$ に対して，当てはまる $\theta$ は 2 個。

ただし，$\theta=\cfrac{\pi}{2}-\cfrac{\pi}{4}=\cfrac{\pi}{4}$ のときは，当てはまる $\theta$ は 1 個。

これらの場合における，$t$ の範囲を求めます。

$-\cfrac{\pi}{4}\leqq\theta<\cfrac{\pi}{4}$ のとき

上の単位円から範囲を考えます。

$-\cfrac{1}{\sqrt{2}}\leqq\sin\Big(\theta-\cfrac{\pi}{4}\Big)<\cfrac{1}{\sqrt{2}}$

式を変形して

$-1\leqq\sqrt{2}\sin\Big(\theta-\cfrac{\pi}{4}\Big)<1$
$-1\leqq t<1$

この範囲で $t$ に当てはまる $\theta$ は 1 個です。

$\cfrac{\pi}{4}\leqq\theta\leqq\cfrac{3}{4}\pi$ のとき

$\cfrac{1}{\sqrt{2}}\leqq\sin\Big(\theta-\cfrac{\pi}{4}\Big)\leqq1$
$1\leqq\sqrt{2}\Big(\theta-\cfrac{\pi}{4}\Big)\leqq\sqrt{2}$
$1\leqq t\leqq\sqrt{2}$

この範囲で $t$ に当てはまる $\theta$ は 2 個です。

ただし，$\theta-\cfrac{4}{\pi}=\cfrac{\pi}{2}$ のとき

$t=\sqrt{2}\sin\cfrac{\pi}{2}$
$=\sqrt{2}$

このとき，$t$ に当てはまる $\theta$ は 1 個です。

グラフに値を書き込んできましょう。

$t=-1$ のとき

$f(\theta)=-\cfrac{1}{\sqrt{2}}(-1)^2-(-1)+\cfrac{1}{\sqrt{2}}=1$

$t=-\cfrac{\sqrt{2}}{2}$ のとき

$f(\theta)=-\cfrac{1}{\sqrt{2}}\Big(-\cfrac{\sqrt{2}}{2}\Big)^2-\Big(-\cfrac{\sqrt{2}}{2}\Big)+\cfrac{1}{\sqrt{2}}$
$=-\cfrac{1}{2\sqrt{2}}+\cfrac{\sqrt{2}}{2}+\cfrac{1}{\sqrt{2}}$
$=\cfrac{3}{2\sqrt{2}}$

$t=1$ のとき

$f(\theta)=-\cfrac{1}{\sqrt{2}}\cdot1^2-1+\cfrac{1}{\sqrt{2}}=-1$

$t=\sqrt{2}$ のとき

$f(\theta)=-\cfrac{1}{\sqrt{2}}(\sqrt{2})^2-\sqrt{2}+\cfrac{1}{\sqrt{2}}$
$=-\cfrac{2}{\sqrt{2}}-\sqrt{2}+\cfrac{1}{\sqrt{2}}=-\cfrac{3}{\sqrt{2}}$

これらの値をグラフに値を書き入れていくと

$1\leqq a\leqq\cfrac{3}{2\sqrt{2}}$ の範囲で，当てはまる $t$ が 2 個あり，このとき，1 個の $t$ に当てはまる $\theta$ はそれぞれ 1 個ずつあるので，結局当てはまる $\theta$ は 2 個あることになります。
また，$-\cfrac{3}{\sqrt{2}}< a\leqq-1$ の範囲では，当てはまる $t$ が 1 個あり，$t$ に当てはまる $\theta$ は 2 個あります。
したがって
$-\cfrac{3}{\sqrt{2}}< a\leqq-1$ または $1\leqq a\leqq\cfrac{3}{2\sqrt{2}}$ (答え)