【数IIベクトル】内積を利用して実数 s, t の値を求める(北海道大2020理系第1問)

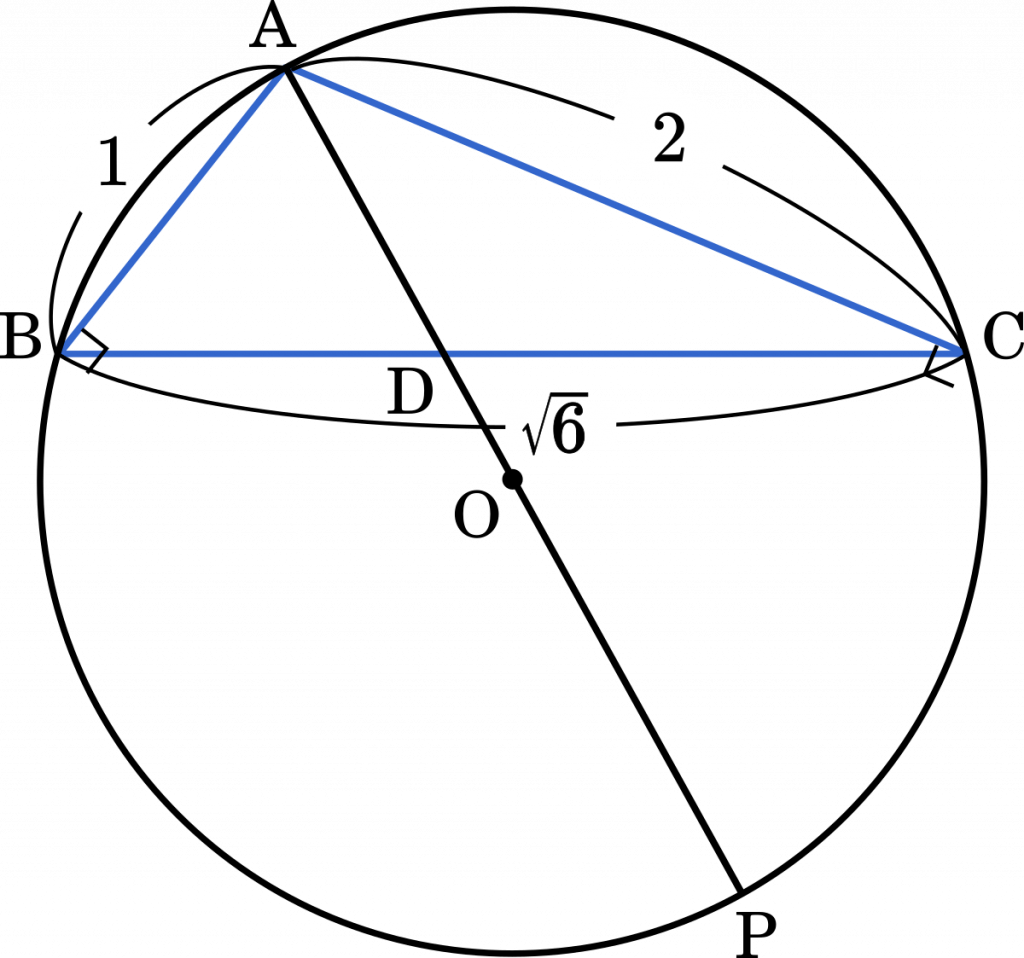
三角形 ABC について
$|\overrightarrow{\text{AB}}|=1,|\overrightarrow{\text{AC}}|=2,|\overrightarrow{\text{BC}}|=\sqrt{6}$
が成立しているとする。三角形 ABC の外接円の中心を O とし，直線 AO と外接円との A 以外の交点を P をする。(北海道大2020)

(1) $\overrightarrow{\text{AB}}$ と $\overrightarrow{\text{AC}}$ の内積を求めよ。
(2) $\overrightarrow{\text{AP}}=s\overrightarrow{\text{AB}}+t\overrightarrow{\text{AC}}$ が成り立つような実数 $s,t$ を求めよ。
(3) 直線 $\overrightarrow{\text{AP}}$ と直線 $\overrightarrow{\text{BC}}$ の交点を D とするとき，線分 AD の長さを求めよ。

余弦定理を使ってコサインを求める

(1)から始めます。

内積を求めるので，公式を使います。

$\vec{a}\cdot\vec{b}=|\vec{a}||\vec{b}|\cos\theta$

よって

$\overrightarrow{\text{AB}}\cdot\overrightarrow{\text{AC}}=|\overrightarrow{\text{AB}}||\overrightarrow{\text{AC}}|\cos\angle{\text{BAC}}$

つまり，$\cos$ の値が必要になるので，余弦定理を使って求めてみます。

$(\sqrt{6})^2=1^2+2^2-2\cdot1\cdot2\cos\angle\text{BAC}$
$6=5-4\cos\angle\text{BAC}$
$4\cos\angle\text{BAC}=-1$
$\cos\angle\text{BAC}=-\cfrac{1}{4}$

したがって

$\overrightarrow{\text{AB}}\cdot\overrightarrow{\text{AC}}=1\cdot2\cdot\Big(-\cfrac{1}{4}\Big)$
$=-\cfrac{1}{2}$ (答え)

s, t を求める

(2)に進みます。

$\overrightarrow{\text{AP}}=s\overrightarrow{\text{AB}}+t\overrightarrow{\text{AC}}$

このままではどうしようもないので，$\overrightarrow{\text{AP}}$ を別な方法で表してみることを考えます。

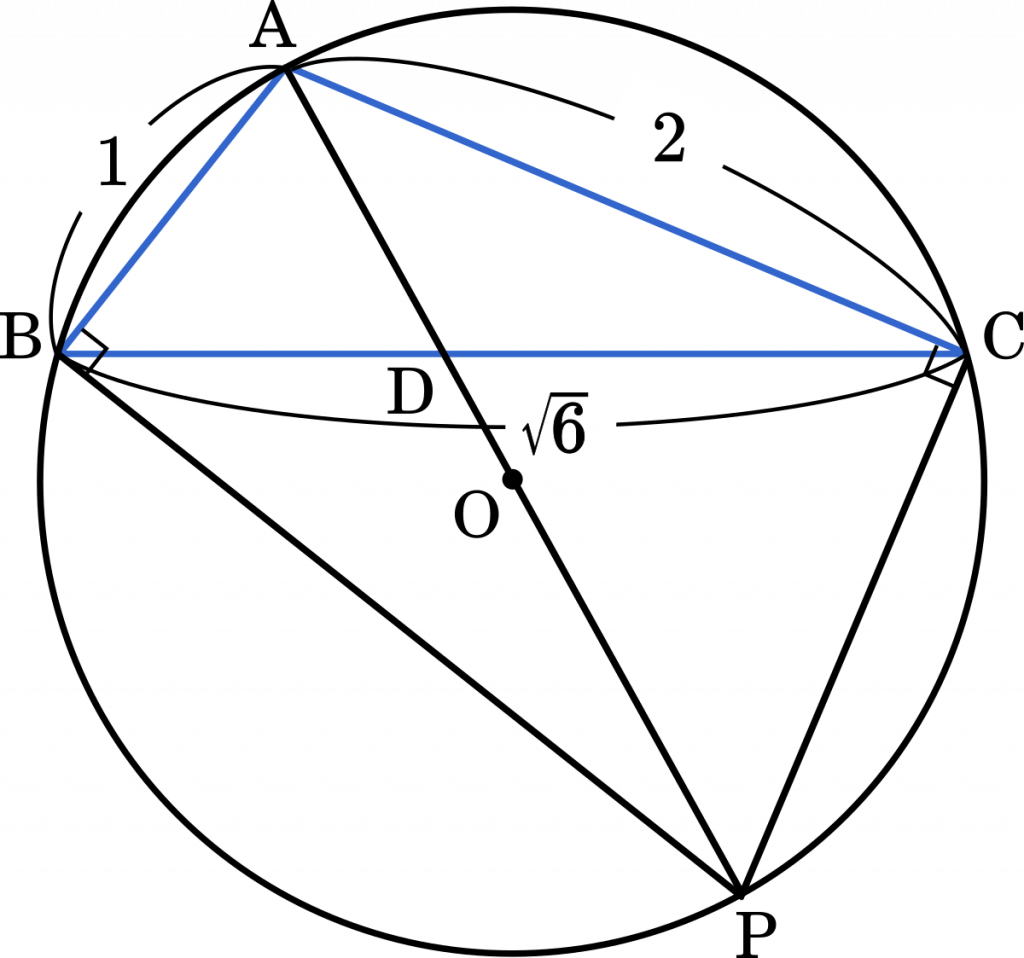
このように直線 BP と CP を引いてみると，AP が円の直径であることから，∠ABP = 90°，∠ACP = 90° となります。ここから，内積 0 の性質が使えそうです。

$\overrightarrow{\text{AP}}=\overrightarrow{\text{AB}}+\overrightarrow{\text{BP}}$ より

$\overrightarrow{\text{BP}}=\overrightarrow{\text{AP}}-\overrightarrow{\text{AB}}$
$=s\overrightarrow{\text{AB}}+t\overrightarrow{\text{AC}}-\overrightarrow{\text{AB}}$
$=(s-1)\overrightarrow{\text{AB}}+t\overrightarrow{\text{AC}}$

また，$\overrightarrow{\text{AP}}=\overrightarrow{\text{AC}}+\overrightarrow{\text{CP}}$ より

$\overrightarrow{\text{CP}}=\overrightarrow{\text{AP}}-\overrightarrow{\text{AC}}$
$=s\overrightarrow{\text{AB}}+t\overrightarrow{\text{AC}}-\overrightarrow{\text{AC}}$
$=s\overrightarrow{\text{AB}}+(t-1)\overrightarrow{\text{AC}}$

$\overrightarrow{\text{AB}}\cdot\overrightarrow{\text{BP}}=0$ より
$(s-1)|\overrightarrow{\text{AB}}|^2+t\overrightarrow{\text{AB}}\cdot\overrightarrow{\text{AC}}=0$
$s-1-\cfrac{t}{2}=0$ ・・・①

$\overrightarrow{\text{AC}}\cdot\overrightarrow{\text{CP}}=0$ より
$s\overrightarrow{\text{AB}}\cdot\overrightarrow{\text{AC}}+(t-1)|\overrightarrow{\text{AC}}|^2=0$
$-\cfrac{s}{2}+4(t-1)=0$ ・・・②

①，②を連立して

①より $s=1+\cfrac{t}{2}$

②に代入

$-\cfrac{1}{2}\Big(1+\cfrac{t}{2}\Big)+4(t-1)=0$
$-\cfrac{1}{2}-\cfrac{t}{4}+4t-4=0$

両辺に 4 をかけて

$-2-t+16t-16=0$
$15t=18$
$t=\cfrac{6}{5}$

$s=1+\cfrac{t}{2}$ に代入して
$s=1+\cfrac{1}{2}\cdot\cfrac{6}{5}=\cfrac{8}{5}$

したがって

$(s,t)=\Big(\cfrac{8}{5},\cfrac{6}{5}\Big)$　（答え）

ベクトルの k 倍を用いて長さを求める

(3)に進みます。

(2)で

$\overrightarrow{\text{AP}}=\cfrac{8}{5}\overrightarrow{\text{AB}}+\cfrac{6}{5}\overrightarrow{\text{AC}}$

が分かりました。

ここから，$\overrightarrow{\text{AD}}$ を考えていきます。

$\overrightarrow{\text{AD}}$ は $\overrightarrow{\text{AP}}$ を短くしたものだから，実数 $k$ を用いて

$\overrightarrow{\text{AD}}=k\overrightarrow{\text{AP}}$
$=\cfrac{8}{5}k\overrightarrow{\text{AB}}+\cfrac{6}{5}k\overrightarrow{\text{AC}}$

と表してみます。

また，点 D は BC 上の点でもあるので

$\cfrac{8}{5}k+\cfrac{6}{5}k=1$

が成り立ちます。

ベクトルの内分点
AB の内分点を C とするとき
$\overrightarrow{\text{OC}}=s\overrightarrow{\text{OA}}+t\overrightarrow{\text{OB}}$
$s+t=1$
が成り立つ。

$\cfrac{14}{5}k=1$
$k=\cfrac{5}{14}$

よって

$\overrightarrow{\text{AD}}=\cfrac{5}{14}\overrightarrow{\text{AP}}$
$=\cfrac{5}{14}\cdot\cfrac{8}{5}\overrightarrow{\text{AB}}+\cfrac{5}{14}\cdot\cfrac{6}{5}\overrightarrow{\text{AC}}$
$=\cfrac{4}{7}\overrightarrow{\text{AB}}+\cfrac{3}{7}\overrightarrow{\text{AC}}$

長さを求めるには，両辺を 2 乗して絶対値を求めると良いです。

$|\overrightarrow{\text{AD}}|^2=\cfrac{16}{49}|\overrightarrow{\text{AB}}|^2+\cfrac{24}{49}\overrightarrow{\text{AB}}\cdot\overrightarrow{\text{AC}}+\cfrac{9}{49}|\overrightarrow{\text{AC}}|^2$
$=\cfrac{16}{49}+\cfrac{24}{49}\Big(-\cfrac{1}{2}\Big)+\cfrac{9}{49}\cdot4$
$=\cfrac{16}{49}-\cfrac{12}{49}+\cfrac{36}{49}$
$=\cfrac{40}{49}$

したがって

$|\overrightarrow{\text{AD}}|=\cfrac{2\sqrt{10}}{7}$　（答え）