【数IIBベクトル】内積って何かの役に立つの？あなたのそっくりさんを内積を用いて数学的に探してみる

高校数学でベクトルを習ったときに，何の意味があるのか最も分からないものが内積です。

問題を解いていくうちに，内積も計算の過程で役立つことがあることに気づくものです。たとえば，内積=0を使って設問で問われているベクトルを求めるような問題を解いたことがあると思います。

とは言え，問題を解いても内積の数字自体が何を意味するのか分からないままで，なんだか納得いかないような気持ちになったかもしれません。

実際のところ，内積の数字そのものは目に見える何かを表しているわけではありません。

それ自体には意味がなくても，それを利用して何かの他の結果を導くことができるもの，それが内積です。

内積を使って得点の傾向を比べる

内積は使い方によって，その値が意味を持つ場合があります。

たとえば，10 点満点の数学と英語のテストを行ったとします。

Aさんは数学 2 点，英語 9 点を取ったとして，それをベクトル $\vec{a}=(2,9)$ と表します。同様に，Bさんは $\vec{b}=(3,8)$，Cさんは $\vec{c}=(10,1)$ とします。

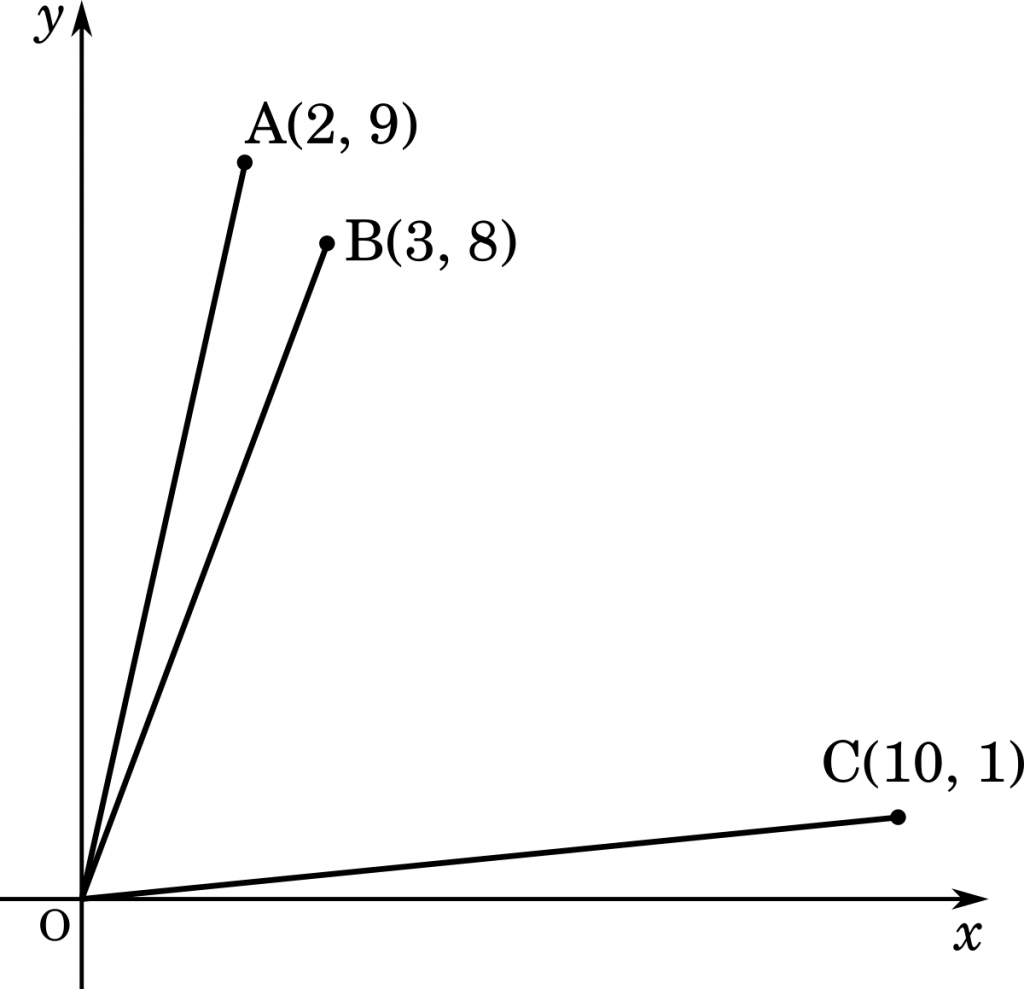
これをグラフで表してみると，AさんとBさんは点の取り方が似ていて，Cさんは他の2人とはあまり似ていないことが分かります。

AさんとBさんが似ていることはグラフの見た目として判断できますが，実際にどの程度似ているかを数字で表す方法を考えてみましょう。

上の図のようにベクトルのなす角を作ってみると，$\vec{a}$ と $\vec{b}$ のなす角は小さく，$\vec{a}$ と $\vec{c}$ のなす角は大きいことが分かります。つまり，角が小さいほどお互いは似ている，角が大きいほどお互いは似ていない，と判断できそうです。

$\vec{a}\cdot\vec{b}=|\vec{a}||\vec{b}|\cos\theta$ ・・・①

$\cos$ の値は，$\cos0\degree$ のとき 1 で，そこから次第に減少して $\cos90\degree$ のときに 0 になります。

実際に計算してみましょう。座標ベクトルの内積は

$\vec{a}=(a_1,a_2),\vec{b}=(b_1,b_2)$ のとき

$\vec{a}\cdot\vec{b}=a_1b_1+a_2b_2$ ・・・②

でした。このとき，①と②は書き方が違うだけで両者は同じものです。

$\vec{a}=(2,9)$，$\vec{b}=(3,8)$，$\vec{c}=(10,1)$ として

$\vec{a}\cdot\vec{b}=2\times3+9\times8=78$
$\vec{a}\cdot\vec{c}=2\times10+9\times1=29$

0 に近い値にはなりませんでしたが，$\vec{a}$ と $\vec{b}$ の内積の方が，$\vec{a}$ と $\vec{c}$ の内積よりも大きな値になりました。つまり，A さんと B さん方が傾向がより似ていると言えます。

こうして，内積を求めることで，誰と誰が似ているかを数字で比べることができます。

３教科で比べてみる

今度は空間ベクトルにチャレンジしましょう。教科を一つ増やして，A さんが数学 2 点，英語 9 点，国語 8 点を取った場合，これを $\vec{a}=(2,9,8)$ と表してみます。同様に，B さんと C さんを，$\vec{b}=(3,8,10)$，$\vec{c}=(10,1,2)$ とします。

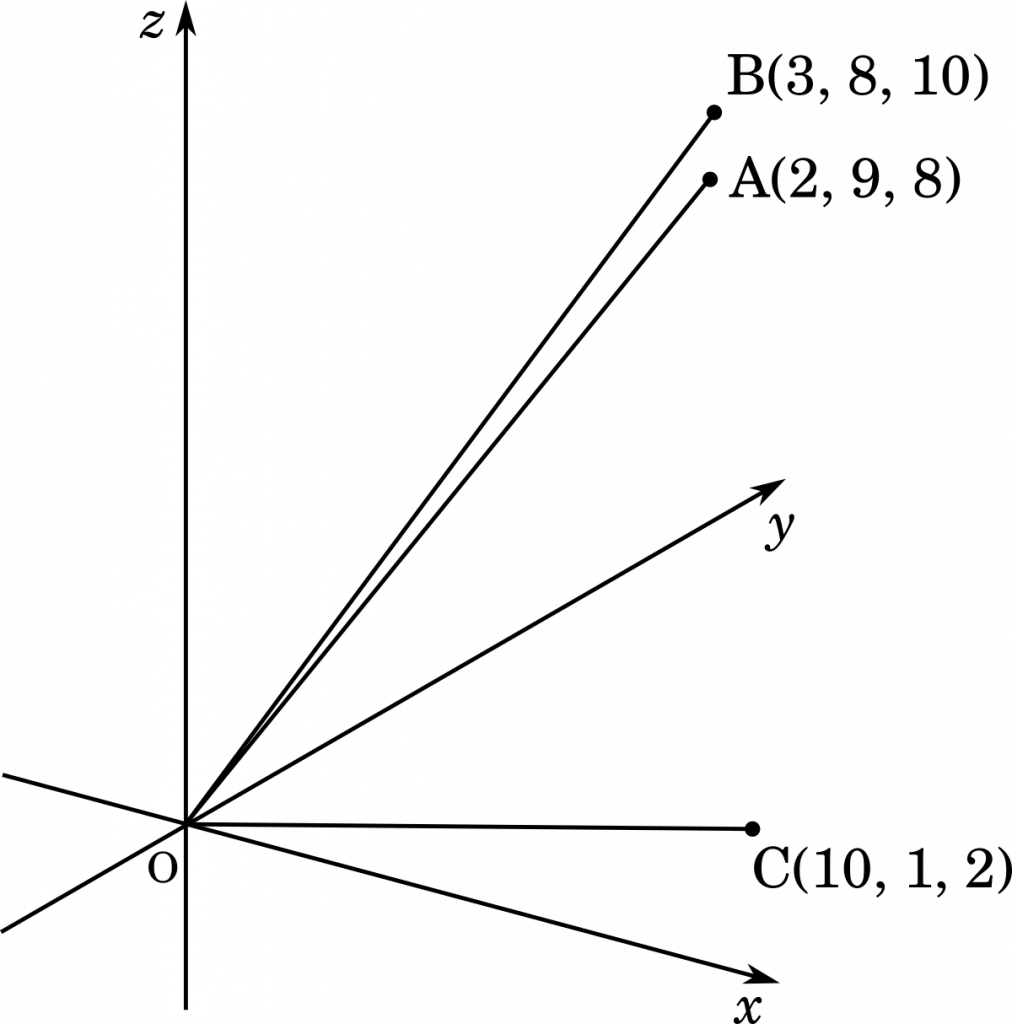
グラフを描いてみると，やはり A さんと B さんの得点の取り方の傾向が似ていて，C さんはあまり似ていないと言えます。同じように内積を求めてみましょう。

$\vec{a}=(2,9,8)$，$\vec{b}=(3,8,10)$，$\vec{c}=(10,1,2)$ として

$\vec{a}\cdot\vec{b}=2\times3+9\times8+8\times10=158$
$\vec{a}\cdot\vec{c}=2\times10+9\times1+8\times2=45$

内積を比べてみると，やはり A さんと B さんの方が傾向が似ていると言えそうです。

こうして，ベクトル同士のなす角に着目することで，内積を用いてベクトル同士の類似度を数字で表すことができることが分かりました。

近似度を数値で表すメリット

高校数学では，ベクトルは３次元までですが，実際にはベクトルの次元はいくらでも増やすことができます。

たとえば，理科と社会と加えた５教科の得点について考えるならば

$\vec{a}=(2,9,8,5,7)$，$\vec{b}=(3,8,10,3,1)$ として

$\vec{a}\cdot\vec{b}=2\cdot3+9\cdot8+8\cdot10+5\cdot3+7\cdot1=180$

と計算できます。

つまり，内積の公式は以下のように拡張できます。

$\vec{a}=(a_1,a_2,\cdots,a_n)$，$\vec{b}=(b_1,b_2,,\cdots,b_n)$ のとき

$\vec{a}\cdot\vec{b}=a_1b_1+a_2b_2+\cdots+a_nb_n$

ここで，近似度を数値で表すメリットが生まれます。

比べる教科が２教科のとき，私たちはそれをグラフとして描くことで傾向が似ているかどうかを見た目で判断することができました。しかし，私たちは 4 次元以上のグラフを実際に描くことはできません。それは想像上にだけ存在する，どこか異世界の話です。

しかしながら，グラフに描くことができない 4 次元以上の世界でも，計算によってその性質を調べることができます。これはベクトルを学ぶ上で重要なポイントの一つです。

ベクトルの次数はいくらでも増やすことができます。

実際ここで取り上げた方法はコンピューターを用いた計算に利用されていて，例えばある 2 つの文章の類似度を測定する，といった目的に利用されています。このとき，ベクトルの次数は数百から数万個，それ以上に及びます。

数学の問題を解いているときには意味があるとは思えない内積ですが，使い方によっては人工知能などのテクノロジーにも応用できる優れた能力を秘めているのです。

コサイン類似度

ここで取り上げた考え方をコサイン類似度と言います。

実際のコサイン類似度はベクトルを単位ベクトルに変換した上で計算を行います。

単位ベクトルとは簡単に言えば，長さが 1 のベクトルのことでした。それぞれのベクトルの長さをそろえることで，内積を対等に比較することができます。

座標ベクトルの場合の計算はこうなります。

$\vec{a}=(2,9)$，$\vec{b}=(3,8)$，$\vec{c}=(10,1)$ のとき

$|\vec{a}|=\sqrt{2^2+9^2}=\sqrt{85}$
$|\vec{b}|=\sqrt{3^2+8^2}=\sqrt{90}$
$|\vec{c}|=\sqrt{10^2+1^2}=\sqrt{101}$

よって

$\cfrac{\vec{a}\cdot\vec{b}}{|\vec{a}||\vec{b}|}=\cfrac{2\cdot3+9\cdot8}{\sqrt{85\cdot90}}=\cfrac{72}{87.46}=0.82$
$\cfrac{\vec{a}\cdot\vec{c}}{|\vec{a}||\vec{c}|}=\cfrac{2\cdot10+9\cdot1}{\sqrt{85\cdot101}}=\cfrac{29}{92.66}=0.31$

したがって，A さんと B さんの方が，A さんと C さんよりも似ていることが分かります。単に内積を比べる場合に比べ，ベクトルの長さをそろえた上で計算する方が，より正確に類似度を測ることができます。