【数Ⅱ剰余の定理】剰余の定理の応用　余りをさらに割っても余りが一致する仕組み

数式 $p(x)$ を $(x-1)^2$ で割ると余りが $4x-5$、$x+2$ で割ると余りが $-4$ である。このとき、$p(x)$ を $(x-1)^2(x+2)$ で割ったときの余りを求めよ。

---

今回ポイントになるのは、式を A で割った余りと、A×B で割った余りをさらに A で割った余りが一致するというところです。

余りをさらに割る、をコインでやってみる

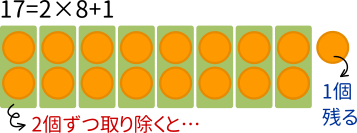
ここにコインが17枚あるとします。コインを2で割ると商は8余りは1です。これは

17 = 2 × 8 + 1

と表すことができます。

今度は17を2×3つまり6で割ってみます。そうすると商は2余りは5になります。そしてこの5を2で割ると商は2余りは1になります。さっきの場合と一致しました。式で表すとこういうことです

17 = ( 2 × 3 ) × 2 + 5

17 = ( 2 × 3 ) × 2 + 2 × 2 + 1

ここで上と下の図を比べてみましょう。

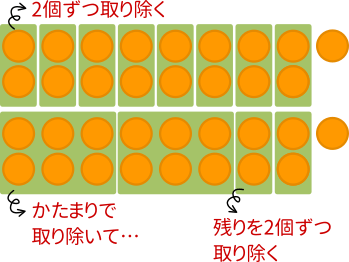
まとめるとこういうことです。17を2で割った余りと、17を2×3で割った余りをさらに2で割った余りは一致する。この考え方を使って実際の問題を解いてみましょう。

剰余の定理を用いて余りを求める

問題に戻りましょう。

数式 $p(x)$ を $(x-1)^2$ で割ると余りが $4x-5$、$x+2$ で割ると余りが $-4$ である。このとき、$p(x)$ を $(x-1)^2(x+2)$ で割ったときの余りを求めよ。

$p(x)=(x-1)^2Q_1(x)+4x-5$ …①
$p(x)=(x+2)Q_2(x)-4$ …②

また、$p(x)$ を $(x-1)^2(x+2)$ で割った余りを $R(x)$ とすると

$p(x)=(x-1)^2(x+2)Q_3(x)+R(x)$ …③

$p(x)$ を $(x-1)^2(x+2)$ で割った余りをさらに $(x-1)^2$ で割った余りは $p(x)$ を $(x-1)^2$ で割った余りと一致する。

$R(x)$ を $(x-1)^2$ で割ったときの商を $k$ とすると、$R(x)=(x-1)^2k+4x-5$ となる。

よって③は

$p(x)=(x-1)^2(x+2)Q_3(x)+(x-1)^2k+4x-5$ …④

同様に，$p(x)$ を $(x-1)^2(x+2)$ で割った余りをさらに $x+2$ で割った余りは $p(x)$ を $x+2$ で割った余りと一致する。

ここで、④に $x=-2$ を代入すると

$p(-2)=(-2-1)^2k+4\cdot(-2)-5=9k-13$

また、②に $x=-2$ を代入すると

$p(-2)=-4$

よって

$9k-13=-4$

よって　$k=1$

$R(x)$ に $k=1$ を代入すると

$(x-1)^2\cdot 1+4x-5$
$=x^2-2x+1+4x-5$
$=x^2+2x-4$　（答え）