【数IIB不等式の表す領域】円と直線の表す領域(北海道大2018)

座標平面上に 3 点 O$(0,0)$，A$(\dfrac{15}{2},0)$，B$(11,11)$ がある。条件

BQ ≧ OQ ≧ 2AQ

を満たす点 Q$(x,y)$ の全体を $D$ とする。(北海道大2018)

(1) $D$ を座標平面上に図示せよ。また，BQ = OQ = 2AQ となるすべての点 Q の座標を求めよ。

(2) $0<p\leqq11$ とし，P を点 $(p,11)$ とする。条件 OQ ≧ PQ を満たす $D$ の点 Q が存在するような $p$ の値の範囲を求めよ。

円の方程式を求める

(1) から始めます。

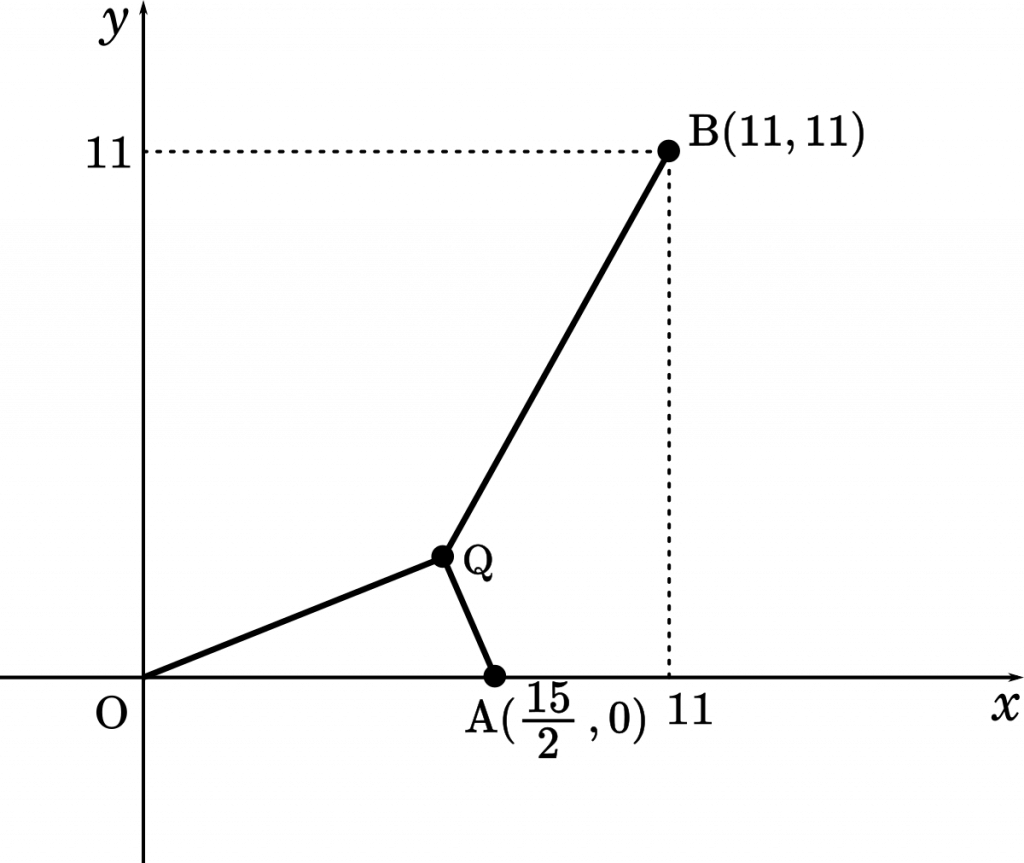
まずは，それぞれの辺の長さに注意してざっくりとした図を描いてみましょう。

辺の長さは三平方の定理を用いて求められるので，あとはそれらを不等式に代入して検討していけば良さそうです。

Q$(x,y)$ として

AQ = $\sqrt{\Big(x-\cfrac{15}{2}\Big)^2+y^2}$
OQ = $\sqrt{x^2+y^2}$
BQ = $\sqrt{(x-11)^2+(y-11)^2}$

平方根のままでは計算できないので，2 乗します。

2AQ ≦ OQ より

$4\text{AQ}^2$ ≦ $\text{OQ}^2$

$4\Big(x-\cfrac{15}{2}\Big)^2+4y^2\leqq x^2+y^2$
$4\Big(x^2-15x+\cfrac{225}{4}\Big)+4y^2-x^2-y^2\leqq0$
$3x^2+3y^2-60x+225\leqq0$

全体を 3 で割って

$x^2+y^2-20x+\cfrac{225}{3}\leqq0$
$(x^2-20x)+y^2+\cfrac{225}{3}\leqq0$
$(x-10)^2-100+y^2+\cfrac{225}{3}\leqq0$
$(x-10)^2+y^2-\cfrac{75}{3}\leqq0$
$(x-10)^2+y^2-25\leqq0$
$(x-10)^2+y^2\leqq5^2$

領域の1つ目ができあがりました。これは中心(10,0)，半径 5 の円の内側ということです。

もう一つの不等式に進みます。

また，OQ ≦ BQ より

$\text{OQ}^2\leqq\text{BQ}^2$
$x^2+y^2\leqq(x-11)^2+(y-11)^2$
$x^2+y^2\leqq x^2-22x+121+y^2-22y+121$
$22x+22y-242\leqq0$
$x+y-11\leqq0$
$y\leqq-x+11$

領域の2つ目ができあがりました。これは直線 $y=-x+11$ の下側ということです。

2 つの領域を重ねると $D$ は

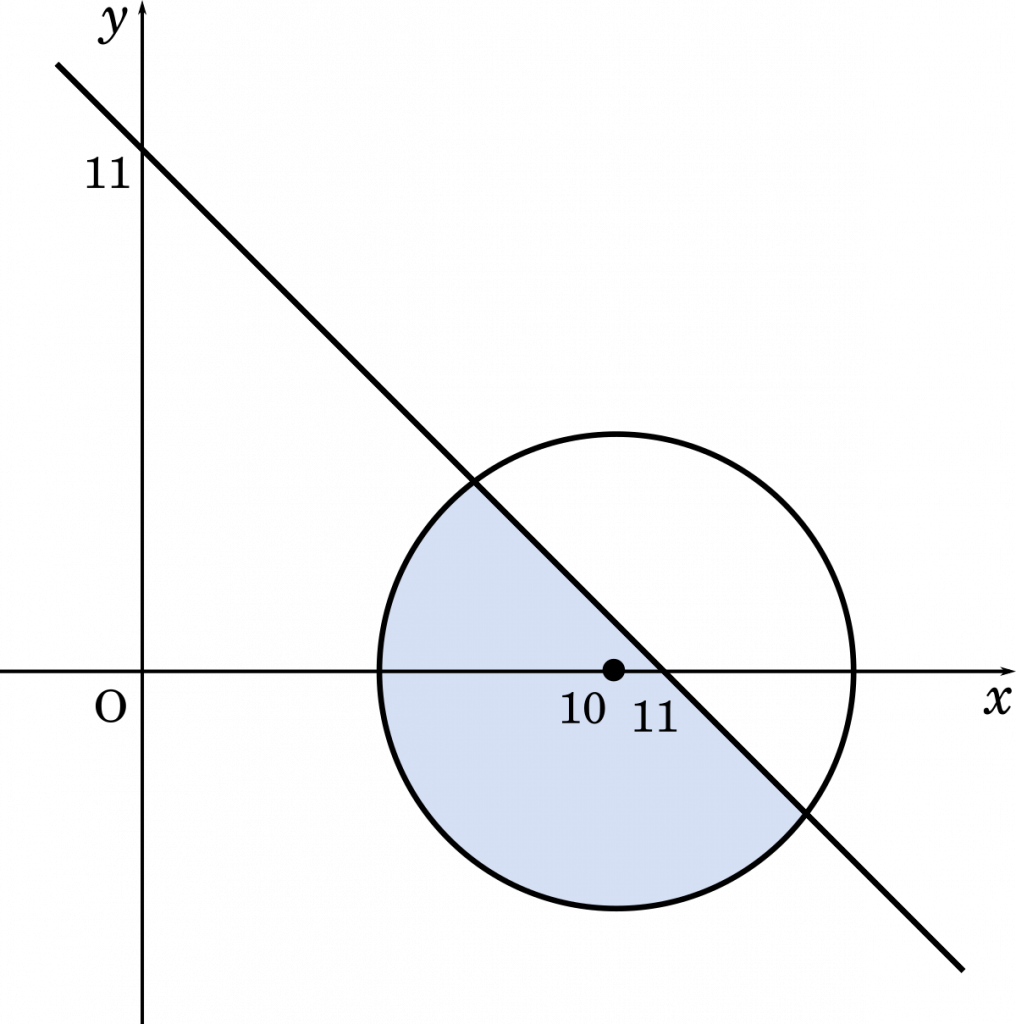
(答え)

次に，BQ = OQ = 2AQ となる点 Q の座標を求めます。

先ほど作った不等式から

2AQ = OQ のとき
$(x-10)^2+y^2=5^2$

OQ = BQ のとき
$y=-x+11$

が成り立つ。

これを連立して $x,y$ を求めます。

$\begin{cases}(x-10)^2+y^2=5^2\cdots\text{①}\\y=-x+11\cdots\text{②}\end{cases}$

②を①に代入して

$(x-10)^2+(-x+11)^2=25$
$x^2-20x+100+x^2-22x+121=25$
$2x^2-42x+196=0$
$x^2-21x+98=0$
$(x-7)(x-14)=0$
$x=7,14$

それぞれ②に代入して

$y=-7+11=4$
$y=-14+11=-3$

したがって

$(x,y)=(7,4),(14,-3)$ (答え)

共有点を利用して領域を求める

(2)に進みます。

とりあえず図を描くとこうなります。

(1)と同じような計算をしてみます。

OQ ≧ PQ より

$\text{OQ}^2\geqq\text{PQ}^2$
$x^2+y^2\geqq(x-p)^2+(y-11)^2$

$\ell:y\geqq-\cfrac{p}{11}x+\cfrac{p^2}{22}+\cfrac{11}{2}$

つまり，$p$ の値によって傾きと切片が変化する直線ができ，その直線の上側に点 Q が存在すればよいということです。

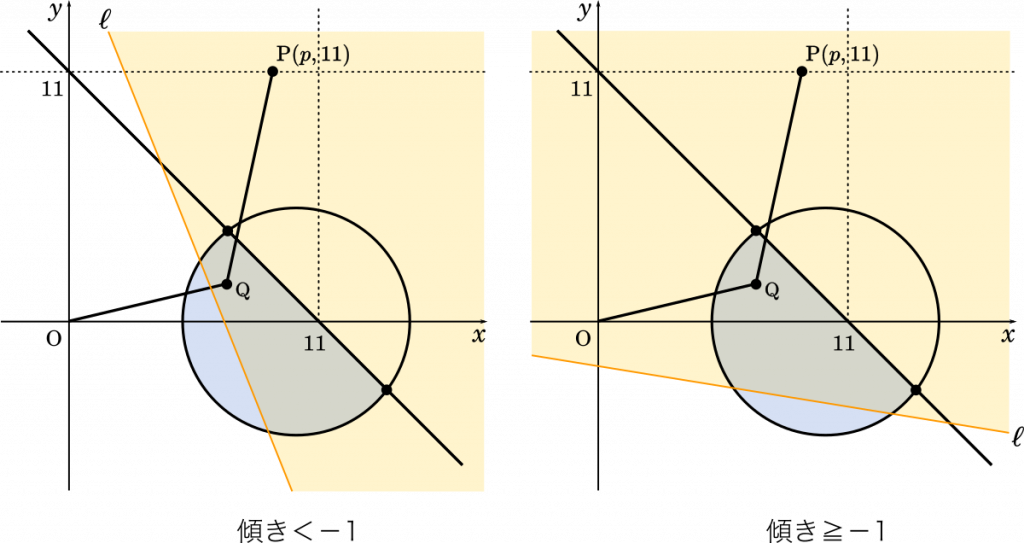
(1)で求めた直線 $y=-x+11$ をもとに考えると，傾きがいずれの場合でも，少なくとも共有点 $(7,4),(14,-3)$ のいずれか一方を領域に含むことが分かります。

(i) 領域に点 $(7,4)$ を含むとき

$4\geqq-\cfrac{p}{11}\cdot7+\cfrac{p^2}{22}+\cfrac{11}{2}$
$88\geqq-14p+p^2+121$
$p^2-14p+33\leqq0$
$(p-1)(p-11)\leqq0$
$3\leqq p\leqq11$

(ii) 領域に点 $(14,-3)$ を含むとき

$-3\geqq-\cfrac{p}{11}\cdot14+\cfrac{p^2}{22}+\cfrac{11}{2}$
$-66\geqq-28p+p^2+121$
$p^2-28p+187\leqq0$
$(p-11)(p-17)\leqq0$
$11\leqq p\leqq17$

$0\leqq p\leqq11$ より $p=11$

こうして式を導いてみると，領域が点 $(14,-3)$ を含むのは，実際には $p=11$ のときだけであり，上でとりあえず描いたようなグラフは実際には作ることができないことが分かります。

実際に存在しうるグラフはこのようなものです。

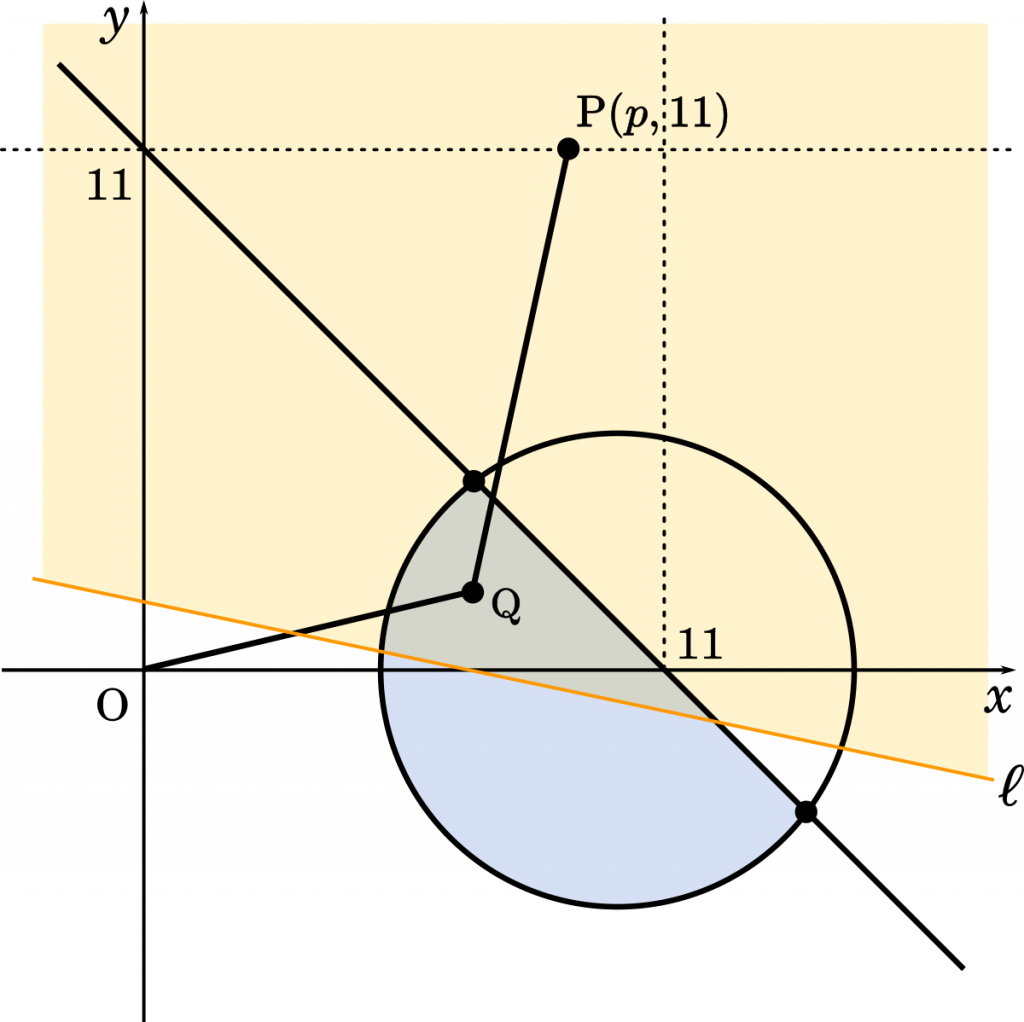
求める範囲は $3\leqq p\leqq11$ または $p=11$ だから

$3\leqq p\leqq 11$ (答え)