【数Ⅱ空間ベクトル】平面に垂線を下す問題 改めて s, t の意味を考える




$s+t=1$ が成り立つ仕組み
まずは、大事なこの関係から押さえましょう。
ベクトル $\overrightarrow{\text{OP}}=s\vec{a}+t\vec{b}$ において、点 P が直線 AB 上にあるとき、$s+t=1$。
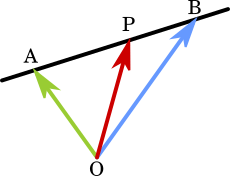


例えば、直線 AB を $3 : 2$ で内分する点 P を考えてみましょう。このとき公式を使えば、
$\displaystyle\frac{2\vec{a}+3\vec{b}}{3+2}=\frac{2}{5}\vec{a}+\frac{3}{5}\vec{b}$
となります。これは図で表すとこういうことです。
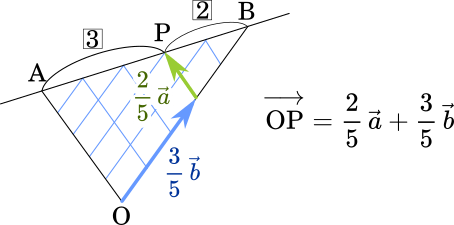


このとき $\displaystyle\frac{2}{5}+\frac{3}{5}=1$ です。いろいろ試してみると分かりますが、内分点だろうと外分点だろうとこの関係は常に成り立ちます。

$s+t=1$ ではないときもある



$s+2t\text{≦}2,\enspace s\text{≧}0,\enspace t \text{≧}0$


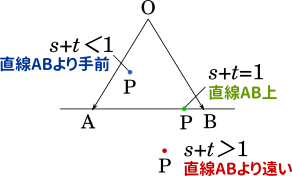


では、問題を解いていきましょう。
$s+t$ が $1$ ではないパターンが出たときには、とりあえず右辺を 1 にするのが鉄則です。両辺を $2$ で割って
$\displaystyle\frac{1}{2}s+t\text{≦}1$
ここで、$\displaystyle s’=\frac{1}{2}s$ とすると
$\displaystyle 2s’=s$
また、$t=t’$ とすると
$\overrightarrow{\text{OP}}=s’2\vec{a}+t’\vec{b}$



よって、
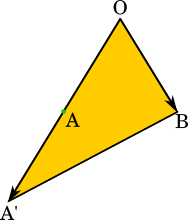
ここで復習は終わりです。$s, t$ が指すもののイメージはつかめたでしょうか。$s, t$ はいろいろな値を取り得るのですが、もう一つ大事なポイントは$\overrightarrow{\text{OP}}=s\vec{a}+t\vec{b}$ の式において、$s, t$ にどんな値を代入してもその点はO, A, B を通る平面上にあるということです。このことを利用して、次の問題を考えていきましょう。
平面に下した垂線のベクトル
ここでようやく本題です。図で表すとこのようなイメージです。
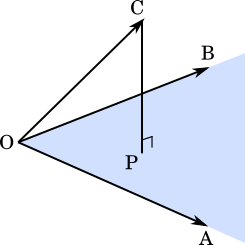
このとき、OA と CP は垂直の関係にあります。同様に OB と CP も垂直です。


いったん、ベクトル CP を求めておきます。
$\overrightarrow{\text{CP}}=\overrightarrow{\text{OP}}-\overrightarrow{\text{OC}}$
$=s\vec{a}+t\vec{b}-\vec{c}$
$=(2s+5t-1,s+2t+5,-t-1)$
次に OA と CP は垂直の関係なので、内積が $0$ になる性質を利用します。
$\overrightarrow{\text{OA}}\cdot\overrightarrow{\text{CP}}=4s+10t-2+s+2t+5$
$5s+12t+3=0\cdots\text{①}$
同様に OB と CP で式を作ります。
$\overrightarrow{\text{OB}}\cdot\overrightarrow{\text{CP}}=10s+25t-5+2s+4t+10+t+1$
$12s+30t+6$
$2s+5t+1=0\cdots\text{②}$
ここで①、②で連立して $s, t$ を求めれば終わりです。
②を変形して
$\displaystyle s=\frac{-5t-1}{2}\cdots\text{③}$
①に代入して
$\displaystyle 5\cdot\frac{-5t-1}{2}+12t+3=0$
$-25t-5+24t+6=0$
$t=1$
③に代入して
$\displaystyle s=\frac{-5-1}{2}=-3$
よって、$(s,t)=(-3,1)$(答え)
・内積=0 を利用して、OA と OB で式を2つ作る。
・連立方程式にもちこんで、$s, t$ を求める。


SNSでシェア