【数II・III】媒介変数は歯車で理解する　大学入学共通テストで使える関数と媒介変数の理解の方法

媒介変数を歯車で理解する

ここに、$x$ という歯車と $y$ という歯車があったとします。この歯車は $x$が１回転するとき $y$ は２回転します。

次にこの歯車の間に $t$ という歯車を挟んでみましょう。

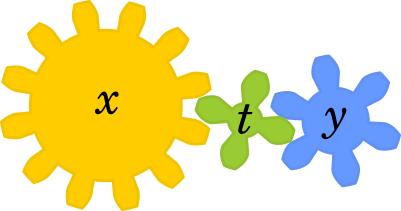
$t$ は $x$ が１回転するときに３回転します。そして、$t$ が３回転するとき $y$ は２回転します。回転数を比で表すと

$x:y=1:2$ かつ $ x:t:y=1:3:2$

という関係が成り立ちます。

この関係から、$t$ が１回転するときには $y$ は$\displaystyle\frac{2}{3}$ 回転すると言うこともできます。今度は $y$ を1回転すれば、$t$は１．５回転して $x$ は０．５回転するはずです。頭の中で歯車を回しながら、歯車同士の関係をつかんでいきましょう。

頭の中で歯車を回していくと、おもしろい性質に気づくでしょう。あいだに $t$ の歯車があろうがなかろうが、$x$ の歯車が１回転するときには $y$ は常に２回転するのです。ここで、媒介変数を使ったからといって、$x$ と $y$ の関係は変わらないという性質を理解しましょう。

歯車の関係を関数で表す

$x$ が１回転するとき $y$ が２回転するという関係を関数として表すと

$y=2x$

となります。$x$ の回転数の２倍が $y$ の回転数になるのです。

ここに $t$ の歯車を入れてみましょう。

$x$ の歯車が１回転するとき $t$ の歯車は３回転するので

$t=3x$　…①

となります。また、$y$ が１回転するとき $t$ は $\displaystyle\frac{3}{2}$ 回転するので

$\displaystyle t=\frac{3}{2}y$　…②

となります。ここで、①、②より

$\displaystyle 3x=\frac{3}{2}y\\y=2x$

結局、もとの $x$ と $y$ の関係に戻りました。

このように、媒介変数を使っても使わなくても $x$ と $y$ の関係は変わらないのです。

媒介変数を使って式を表現する

媒介変数を使う事例の一つを紹介しましょう。半径１の円において、円周上のある点を $(x,y)$ とするとき、三平方の定理より $x^2+y^2=1$ の関係が成り立ちます。

しかしこの関係を実際に使う場合には、$x$ と $ y $ の値が分かっている必要があります。例えば、$\displaystyle x=\frac{\sqrt{3}}{2}$ で $\displaystyle y=\frac{1}{2}$ なら、$\displaystyle \left(\frac{\sqrt{3}}2\right)^2+\left(\frac{1}{2}\right)^2=1$ となるので、三平方の定理がちゃんと成り立っていることが確認できます。

しかし、$x,y$ の値がはっきりしない場合にはどうすればよいでしょう。$x^2+y^2=1$ は $\sqrt{1-x^2}$ と変形できます。一応、$x$ の値によって $y$ の値を求めることはできるのですが、2乗や平方根がでてくるので $x$ の値によっては計算がかなりタイヘンなことになりそうです。

ここで、媒介変数 $\theta$ が登場します。

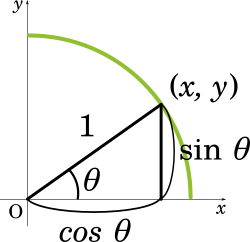
このとき、$x=\cos\theta$、$y=\sin\theta$ となるので$\sin^2\theta+\cos^2\theta=1$ となります。これは、おなじみの三角比の公式ですが、考えてみればこれは三平方の定理を表しているとも言えます。このように、媒介変数を使うことで二つの文字 $x,y$ で表す式を一つの文字 $\theta$ で表す式に変換できます。$\displaystyle (x,y)=\left(\frac{\sqrt{3}}{2},\frac{1}{2}\right)$ には$\displaystyle\theta=\frac{\pi}{6}$ という別の表し方があるということです。

つまり媒介変数の利点とは、文字の数を減らしたり、値を代入するのが難しい文字式を別な方法で表して値を代入しやすくするところにあるのです。