【数Ⅱ高次方程式】解の一つが与えられた4次方程式の解き方と因数定理の仕組み
$x^4+6x^3+29x^2-28x+35=0$
の解の一つが $\cfrac{1+\sqrt{3}i}{2}$ のとき,残りの解をすべて求めよ。

これどうやって解こうか?

$x$ に数字入れて 0 にするんですよね。

確かにその方法あるけど,今回は $x$ に 1 とか -1 とか代入しても左辺が 0 にならない。ようするに,そのときの 1 とか -1 とかって解の一つってことだよね。でも今回は解の一つとして $\cfrac{1+\sqrt{3}i}{2}$ が与えられている。だから,それを使ってみる。

はあ。
複素数の解の性質
一般にある高次方程式の解の一つが複素数であるとき,その共役な複素数も解である。

これ,教科書で習うヤツ。

ああ,何となく覚えあるかも。

ということは $\cfrac{1-\sqrt{3}i}{2}$ も解であるといえる。4次方程式は解が4つできるはずだから,あと二つを求めればよい。

でも因数定理使えないですよ。
共役な複素数を因数定理に当てはめる

実はここから因数定理を使う。
$f(x)=\Big(x-\cfrac{1+\sqrt{3}i}{2}\Big)\Big(x-\cfrac{1-\sqrt{3}i}{2}\Big)Q(x)=0$

ここで $Q(x)$ は割り算したときの商を表すヤツ。

これどういうことでしたっけ?

$x$ に $\cfrac{1+\sqrt{3}i}{2}$ を代入すると最初のカッコが $\Big(\cfrac{1+\sqrt{3}i}{2}-\cfrac{1+\sqrt{3}i}{2}\Big)$ ってなって 0 になる。0 のかけ算だから式全体が 0 になる。$\cfrac{1-\sqrt{3}i}{2}$ のときも同様で $x$ にこれを代入すると,今度は真ん中のカッコが 0 になるよね。

なりますね。

で,これはもとの式を $\Big(x-\cfrac{1+\sqrt{3}i}{2}\Big)\Big(x-\cfrac{1-\sqrt{3}i}{2}\Big)$×(式) の形に因数分解できるって意味なの。これが因数定理。

何かピンとこない。
因数定理の仕組み

例えば $x^2-3x+2=0$ という方程式があったとする。これは $(x-1)(x-2)=0$ と因数分解して $x=1,2$ が解になる。言い換えると,式に $x=1$ を代入すると $(1-1)(1-2)=0$ ってなって恒等式が成り立つ。だから,$x=1$ は解であるっていう解釈だった。

でしたね。

これは逆に言うと,方程式は($x$-解)で割り切れるってことでもあるよね。これも例えばだけど,式を解じゃない数,$(x-3)$ で割ってみる。実際ひっ算でやってみると,商が $x$ で余り 2 になる。つまり$x^2-3x+2=(x-3)x+2=0$となるよね。

なりますね。

ここから分かるのは,解じゃない数を使って割っても余りがでる,つまり割り切れないってこと。

なんで割り切れないの?

解である 1 や 2 を代入しても $(x-3)x$ は $(1-3)\times1$ とか $(2-3)\times2$ になるから 0 にならないでしょ? だから余りの項があって,それを足すか引くかしないと式全体で 0 にはならない。

でも,式を $(x-1)$ で割れば $(x-1)Q(x)$ ってなって,$Q(x)$ がどんな式だろうと $x=1$ を代入すれば式は 0 になる。つまり,余りの項がいらない。「余りがない=割り切れる」っていう理屈。

確かに。でも分かりにくい。

そうそう。因数定理って三次方程式解くときよく使うけど,理屈自体は直感的に分かりにくいよね。

だからとりあえず,方程式は解が分かってると ($x$-解)の積に直せるってのだけ覚えて,そういうものだと納得するもの。細かいことは気にしない。

りょーかいです。
ひっ算で割ってみる
$f(x)=\Big(x-\cfrac{1+\sqrt{3}i}{2}\Big)\Big(x-\cfrac{1-\sqrt{3}i}{2}\Big)Q(x)=0$
展開して
$\Big\{x^2-\Big(\cfrac{1+\sqrt{3}i}{2}+\cfrac{1-\sqrt{3}i}{2}\Big)x+\cfrac{1+\sqrt{3}i}{2}\cdot\cfrac{1-\sqrt{3}i}{2}\Big\}Q(x)=0$
$\Big\{x^2-\cfrac{1+\sqrt{3}i+1-\sqrt{3}i}{2}x+\cfrac{(1+\sqrt{3}i)(1-\sqrt{3}i)}{4}\Big\}Q(x)=0$
$\Big\{x^2-\cfrac{2}{2}x+\cfrac{1-(\sqrt{3})^2(-1)}{4}\Big\}Q(x)=0$
$(x^2-x+1)Q(x)=0$

ここ計算ミスしやすいから注意。

再びさっきの式に戻るけど,実際にひっ算使って割っていく。理屈からすれば割り切れるはず。
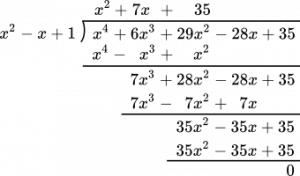
よって
$f(x)=(x^2-x+1)(x^2+7x+35)=0$

で,ここから?

これがイコール 0 になる場合だから,$x^2-x+1=0$ または $x^2+7x+35=0$ ということになる。あとは普通に二次方程式を公式放り込んで解けばよい。
$x=\cfrac{1\pm\sqrt{3}i}{2}$,$\cfrac{-7\pm\sqrt{91}i}{2}$

因数定理の式作るところまでいったらあとは大したことないかも。

そうそう,解が二つ分かったとき ($x$-解)($x$-解)×$Q(x)$ の形がひらめくかどうかの問題。経験値ためてレベルアップしてね。
SNSでシェア