【数Ⅰ二次関数】平行移動の符号はなぜ反対になるのか　答えは見方が逆だから

二次関数の平行移動で符号が逆になるのがイマイチ納得いかないです。

それ、見てる向きが逆だからよ。

どういうこと？

説明していくね。

二次関数の平行移動は原点に戻した場合の関係性で考える

$y=(x-2)^2+5$ のグラフを考えてみましょう。

ここで、教科書のおさらい。

$y=(x-2)^2+5$ の $+5$ を左辺に移項すると、このような式になります。

$y-5=(x-2)^2$

こんな感じで、どっちも符号が反対になる。

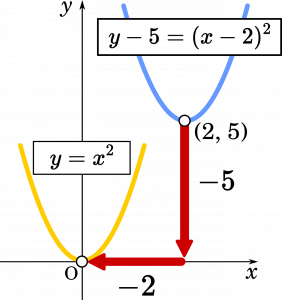
青のグラフ $y-5=(x-2)^2$ 上の頂点 $(2,5)$ は $x$ を $-2$、$y$ を $-5$ 移動すると黄色のグラフ上の頂点（原点）に戻ります。同様に点 $(4,9)$ なら移動すると黄色の$(2,4)$ になります。

二次関数 $y-5=(x-2)^2$ の $x$ に何かの値を代入すると $y$ の値が決まります。このときの $x$ と $y$ の位置関係は $x$ から$2$、$y$ から $5$ 引くと、$y=x^2$ における $x$ と $y$ の位置関係と同じになる、という理屈です。

$y+5=(x+2)^2$ じゃダメなの？そっちが分かりやすいけど。

ダメよ。ここで代入する $x$ の値は青のグラフ上の点だから。引き算で青から黄色のグラフに持っていくの。$y+5=(x+2)^2$ だと黄色のグラフから青のグラフに移動する話になるでしょ？それだと話が逆。

ああ、そういうこと。

見方を変えると方程式が見えてくる

何となく理屈分かったけど、何で原点に戻すの？

頂点を原点に戻すと $y=x^2$ という簡単な形になるからだよ。二次関数のグラフはいくつでも作れるけど、頂点を原点に移動すれば全部同じ形で表せる。

さっきの $y-5=(x-2)^2$ だって、$y-5=Y,x-2=X$ と置きかえてやると $Y=X^2$ ってなって基本の形で表せるでしょ？二次関数なら全部この形になるから便利だよね。

色々考え方あるんですね。

方程式で移項すると符号が逆になるのも、式として表現するときに見方によってプラスなのかマイナスなのか説明の仕方が変わってるってことなのよ。方程式の本質みたいな話。例えば、$y=3x+4$ を、「$x$ を $3$ 倍して $4$ を足した値は $y$ に等しい」と説明するか、$+4$ を移項して $y-4=3x$ として、「$x$ を $3$ 倍した値は $y$ から $4$ を引いた値と等しい」と説明するかの違い。どっちも同じことなんだけど、式の形や見方を変えれば色んな説明の方法が出てくる。

方程式けっこう奥深いですね。

方程式ってうまく説明がつかないときに観点を変えると見えてくる時があるから、特に逆向きで見てみるっていう手は色んな場面で試してみるといいよ。今回も教科書の説明と別な方法でやってるけど、教科書で分からなかったらこうやって見方を変えてみるっていう手もあるよっていう一つの事例だよね。こういう作業は論理的思考のビルドアップにつながるからがんばってみてね。