【数IA】格子点を数える(境界を含まない場合)(千葉大2016第3問)
座標平面上に 5 点 O(0,0),A(5,0),B(0,11),P($m$,0),Q(0,$n$)をとる。ただし,$m$ と $n$ は $1$ ≦ $m$ ≦ $5$,$1$ ≦ $n$ ≦ $11$ を満たす整数とする。
(1) 三角形 OAB の内部に含まれる格子点の個数を求めよ。ただし,格子点とは $x$ 座標と $y$ 座標がともに整数である点のことであり,内部には辺上の点は含まれない。
(2) 三角形 OPQ の内部に含まれる格子点の個数が三角形 OAB の内部に含まれる格子点の個数の半分になるような組 ($m$,$n$) をすべて求めよ。
格子点の問題はだいたいの場合は地道に格子点の数を数えていけば解決できます。$x$ の値ごとに縦方向に格子点を数えていきましょう。
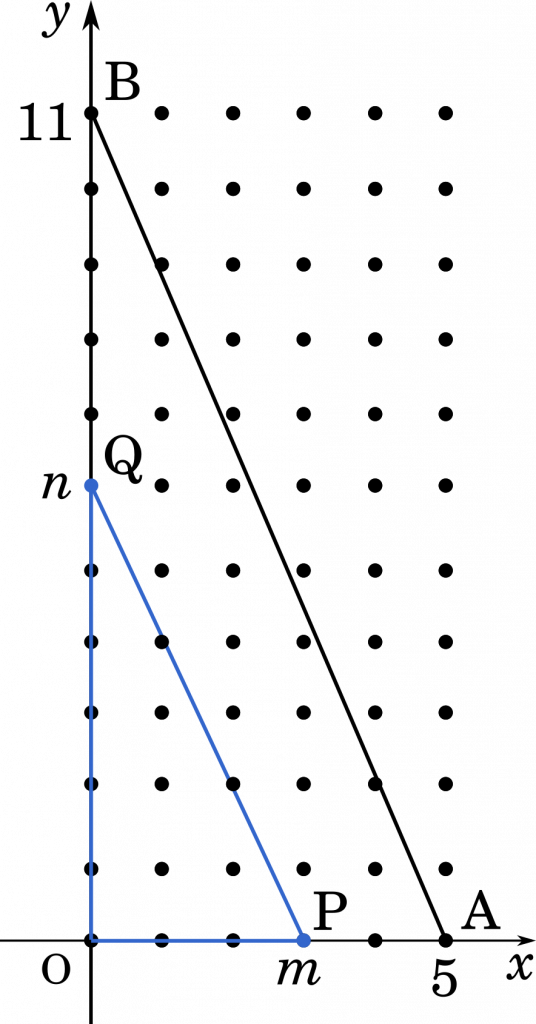
境界を含まない場合
(1)から進めます。まず,直線 AB の式を求めます。
A(5,0),B(0,11) より,直線 AB は
$y=-\cfrac{11}{5}x+11$
ここから,順番に格子点を数えていきますが,今回は領域の境界上の点は数えないことに注意します。たとえば,$x=0$ のとき直線 OB 上にある格子点は数えません。同様に $x=5$ のときも数えないので,数える範囲は $x$ が $1$ から $4$ の間です。
$x=1$ のとき,$y=-\cfrac{11}{5}+11=\cfrac{44}{5}$
$8$ < $\cfrac{44}{5}$ < $9$ だから,含まれる格子点は $8$ 個です。

$x=2$ のとき,$y=-\cfrac{22}{5}+11=\cfrac{33}{5}$
よって,$6$ 個。
$x=3$ のとき,$y=-\cfrac{33}{5}+11=\cfrac{22}{5}$
よって,$4$ 個。
$x=4$ のとき,$y=-\cfrac{44}{5}+11=\cfrac{11}{5}$
よって,$2$ 個。
したがって,含まれる格子点は
$8+6+4+2=20$ 個 (答え)
あたりをつけて地道に数える
(2)に進みます。
(1)が 20 個だったので,ここでは領域に含まれる格子点が $10$ 個あればよいことになります。



直線 PQ の式は
$y=-\cfrac{n}{m}x+n$
$m$ が $0$ から $5$ までを順番に考えていきます。
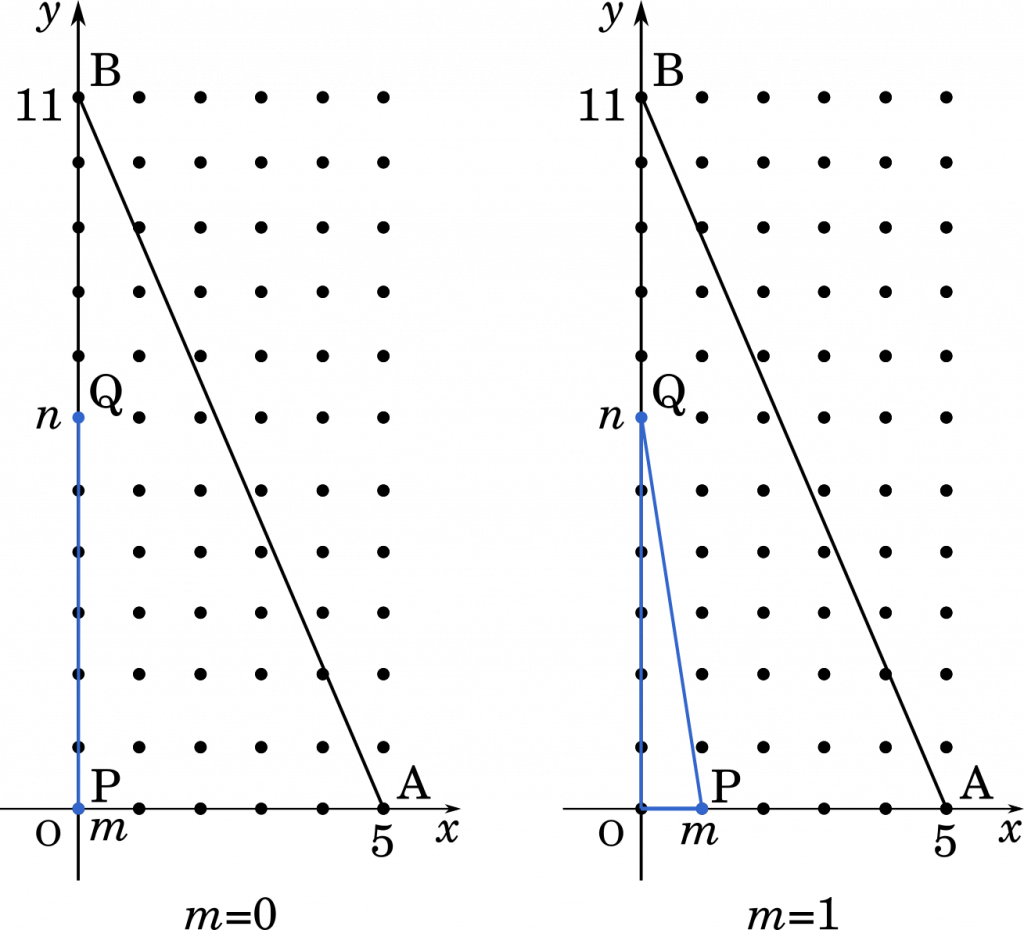
(i) $m=0$ のとき
直線 PQ は $y$ 軸上にあり,含まれる格子点は $0$ 個。
(ii) $m=1$ のとき
上の図のように,$n$ の値に関係なく含まれる格子点は $0$ 個です。
(iii) $m=2$ のとき
$x=2$ に含まれる格子点は $0$ 個です。また,$x=1$ に含まれる格子点は(1)より最大で $8$ 個だから,合計で $10$ になることはありません。
(iv) $m=3$ のとき
$y=-\cfrac{n}{3}x+n$
$x=1$ のとき $y=-\cfrac{n}{3}+n=\cfrac{2n}{3}$
$x=2$ のとき $y=-\cfrac{n}{3}\cdot2+n=\cfrac{n}{3}$
もし,$n=11$ だとすると,$\cfrac{2\cdot11}{3}=\cfrac{22}{3}$ だから $7$ 個。$\cfrac{11}{3}$ の場合は 3 個です。したがって,$7+3=10$ 個となるので,解の一つは $(m,n)=(3,11)$ です。
次に,$n=10$ のとき,$\cfrac{20}{3}$ で $6$ 個。$\cfrac{10}{3}$ で $3$ 個。合計 $9$ 個です。あとは,$n$ の値が小さくなるにつれて,合計の値も小さくなるので,考えなくてもよいでしょう。
$(v)$ $m=4$ のとき
$y=-\cfrac{n}{4}x+n$
$x=1$ のとき $y=-\cfrac{n}{4}+n=\cfrac{3n}{4}$
$x=2$ のとき $y=-\cfrac{2n}{4}+n=\cfrac{n}{2}$
$x=3$ のとき $y=-\cfrac{3n}{4}+n=\cfrac{n}{4}$

$n=10$ のとき $\cfrac{30}{4},\cfrac{10}{2},\cfrac{10}{4}$ で $7+4+2=13$ 個。
$n=9$ のとき $\cfrac{27}{4},\cfrac{9}{2},\cfrac{9}{4}$ で $6+4+2=12$ 個。
$n=8$ のとき $\cfrac{24}{4},\cfrac{8}{2},\cfrac{8}{4}$ で $5+3+1=9$ 個。
格子点が $10$ 個になる場合は存在しない。
(vi) $m=5$ のとき
$y=-\cfrac{n}{5}x+n$
$x=1$ のとき $y=-\cfrac{n}{5}+n=\cfrac{4n}{5}$
$x=2$ のとき $y=\cfrac{3n}{5}$
$x=3$ のとき $y=\cfrac{2n}{5}$
$x=4$ のとき $y=\cfrac{n}{5}$

$n=7$ のとき $\cfrac{28}{5},\cfrac{21}{5},\cfrac{14}{5},\cfrac{7}{5}$ で $5+4+2+1=12$ 個。
$n=6$ のとき $\cfrac{24}{5},\cfrac{18}{5},\cfrac{12}{5},\cfrac{6}{5}$ で $4+3+2+1=10$ 個。
よって,解の一つは $(m,n)=(5,6)$
$n=5$ のとき $\cfrac{20}{5},\cfrac{15}{5},\cfrac{10}{5},\cfrac{5}{5}$ で $3+2+1+0=6$ 個。
したがって,$(m,n)=(3,11),(5,6)$ (答え)
SNSでシェア