【数IA三角比】回転した長方形が重複する面積を求める(千葉大2012第7問)

引き算ですよね。

そうね。図を描いてみると分かるけど，長方形の面積から三角形を引いていく感じ。また，同じ大きさの三角形が２つずつあって，ようはそれらの三角形の面積さえ分かれば答えが出る。

んー，長さ分かりそうで分からない。

解き方は一つじゃないけど，今回はアイデアをなるべくシンプルに持っていく。その代わり計算量多いかも。

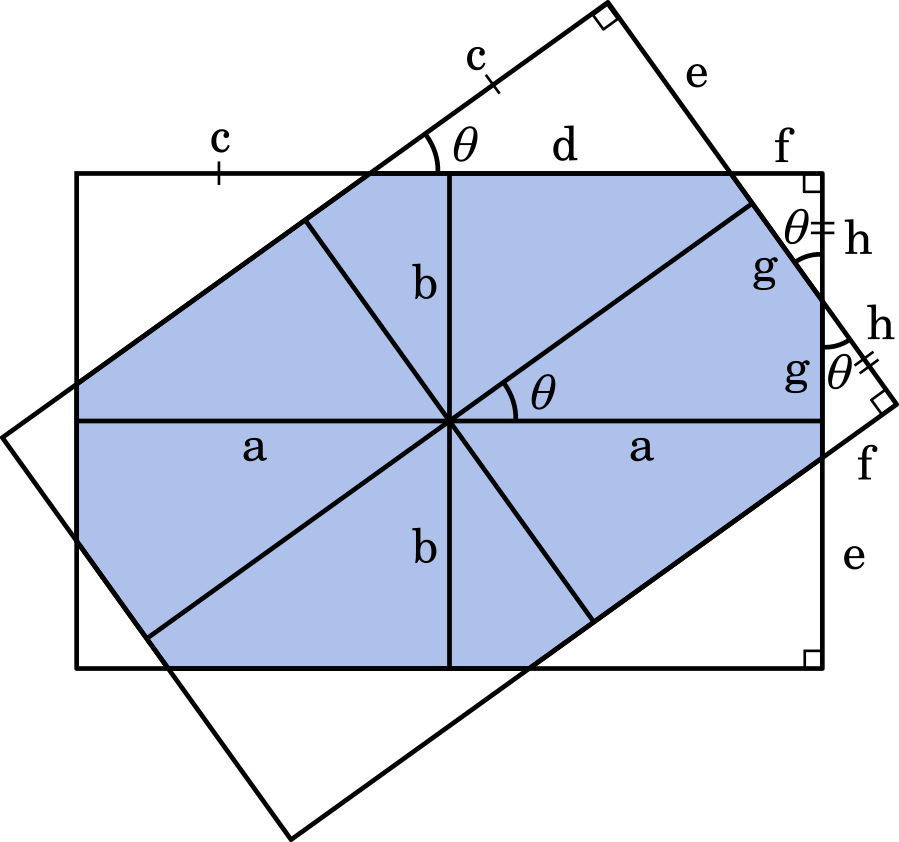
連立方程式を導く

まず，面積を求める式はこのようになります。
$S(\theta)=2a\cdot2b-2\cdot\cfrac{1}{2}ce-2\cdot\cfrac{1}{2}fh$
$=4ab-ce-fh$
また，図より，長方形の横の長さ $2a$ と縦の長さ $2b$ はこのようになります。
$c+d+f=2a$ ・・・①
$e+g+h=2b$ ・・・②
さらに，大きな三角形から次の関係を導くことができます。
$d\sin\theta=e$，$d\cos\theta=c$

$\sin\theta$ は $\cfrac{高さ}{斜辺}$ だから斜辺×$\cfrac{高さ}{斜辺}$＝高さ。$\cos\theta$ は $\cfrac{\text{底辺}}{\text{斜辺}}$ だから，斜辺×$\cfrac{\text{底辺}}{\text{斜辺}}$＝底辺。

同様に小さな三角形では
$g\sin\theta=f$，$g\cos\theta=h$
これらを $S(\theta)$ に代入すると
$S(\theta)=4ab-d\cos\theta\cdot d\sin\theta-g\sin\theta\cdot g\cos\theta$
$S(\theta)=4ab-(d^2+g^2)\sin\theta\cos\theta$
また，①，②は
$d\cos\theta+d+g\sin\theta=2a$
$d(1+\cos\theta)+g\sin\theta=2a$
$g=\cfrac{2a-d(1+\cos\theta)}{\sin\theta}$ ・・・③
$d\sin\theta+g+g\cos\theta=2b$
$d\sin\theta+g(1+\cos\theta)=2b$
$d=\cfrac{2b-g(1+\cos\theta)}{\sin\theta}$ ・・・④

似たような形になった。

これから連立解くけど，形がそっくりってのは計算する上で手がかりになる。

③を変形して
$g=\cfrac{2a}{\sin\theta}-d\cfrac{1+\cos\theta}{\sin\theta}$
③に④を代入して
$g=\cfrac{2a}{\sin\theta}-\cfrac{2b-g(1+\cos\theta)}{\sin\theta}\cdot\cfrac{1+\cos\theta}{\sin\theta}$
$g$ を左側にまとめていく
$g\sin^2\theta=2a\sin\theta-\{2b-g(1+\cos\theta)\}(1+\cos\theta)$
$g\sin^2\theta=2a\sin\theta-2b(1+\cos\theta)+g(1+\cos\theta)^2$
$g\sin^2\theta-g(1+\cos\theta)^2=2a\sin\theta-2b(1+\cos\theta)$
$g\sin^2\theta-g(1+2\cos\theta+\cos^2\theta)=2a\sin\theta-2b(1+\cos\theta)$
$g(\sin^2\theta-1-2\cos\theta-\cos^2\theta)=2a\sin\theta-2b(1+\cos\theta)$

左辺が $\sin$ と $\cos$ が混ざってゴチャゴチャしているので $\cos$ に合わせみます。

三角比の公式より $\sin^2\theta=1-\cos^2\theta$ だから
$g(1-\cos^2\theta-1-2\cos\theta-\cos^2\theta)=2a\sin\theta-2b(1+\cos\theta)$
$g(-2\cos^2\theta-2\cos\theta)=2a\sin\theta-2b(1+\cos\theta)$
$g(\cos^2\theta+\cos\theta)=b(1+\cos\theta)-a\sin\theta$
$g=\cfrac{b(1+\cos\theta)-a\sin\theta}{\cos\theta(1+\cos\theta)}$

ここから，$S(\theta)$ にあてはめるために $g^2$ を求めます。

$g^2=\cfrac{b^2(1+\cos\theta)^2-2ab\sin\theta(1+\cos\theta)+a^2\sin^2\theta}{\cos^2\theta(1+\cos\theta)^2}$

次に $d$ を求めますが，$g$ の式の文字を入れ替えたものだから

$d^2=\cfrac{a^2(1+\cos\theta)^2-2ab\sin\theta(1+\cos\theta)+b^2\sin^2\theta}{\cos^2\theta(1+\cos\theta)^2}$
$d^2+g^2=\cfrac{(a^2+b^2)(1+\cos\theta)^2-4ab\sin\theta(1+\cos\theta)+(a^2+b^2)\sin^2\theta}{\cos^2\theta(1+\cos\theta)^2}$
$=\cfrac{(a^2+b^2)(1+2\cos\theta+\cos^2\theta)-4ab\sin\theta(1+\cos\theta)+(a^2+b^2)\sin^2\theta}{\cos^2\theta(1+\cos\theta)^2}$
$=\cfrac{(a^2+b^2)(1+2\cos\theta+\cos^2\theta+\sin^2\theta)-4ab\sin\theta(1+\cos\theta)}{\cos^2\theta(1+\cos\theta)^2}$

上でやったことと同じように $\sin$ を $\cos$ に合わせます

$=\cfrac{(a^2+b^2)(1+2\cos\theta+\cos^2\theta+1-\cos^2\theta)-4ab\sin\theta(1+\cos\theta)}{\cos^2\theta(1+\cos\theta)^2}$
$=\cfrac{(a^2+b^2)(2+2\cos\theta)-4ab\sin\theta(1+\cos\theta)}{\cos^2\theta(1+\cos\theta)^2}$
$=\cfrac{2(a^2+b^2)(1+\cos\theta)-4ab\sin\theta(1+\cos\theta)}{\cos^2\theta(1+\cos\theta)^2}$
$=\cfrac{2(a^2+b^2)-4ab\sin\theta}{\cos^2\theta(1+\cos\theta)}$

これを $S(\theta)$ に代入すると

$S(\theta)=4ab-(d^2+g^2)\sin\theta\cos\theta$
$=4ab-\cfrac{2(a^2+b^2)\sin\theta-4ab\sin^2\theta}{\cos\theta(1+\cos\theta)}$

通分して

$=\cfrac{4ab\cos\theta(1+\cos\theta)-2(a^2+b^2)\sin\theta+4ab\sin^2\theta}{\cos\theta(1+\cos\theta)}$
$=\cfrac{4ab\{\cos\theta+\cos^2\theta+\sin^2\theta\}-2(a^2+b^2)\sin\theta}{\cos\theta(1+\cos\theta)}$
$=\cfrac{4ab(1+\cos\theta)-2(a^2+b^2)\sin\theta}{\cos\theta(1+\cos\theta)}$ (答え)