【数Ⅰ集合と命題】レポーターは標高何mにいる？　必要条件と十分条件の考え方

つまり、$x>4000$ なら $x>2000$ は必ず成り立つ。「必ず成り立つ」は言い換えると「条件を十分満たしている」ということだから、十分条件です。

必要条件の考え方

今度は「今、標高2000m以上に来てます！」と言われても、標高4000m以上にいるとは限らないですよね。実際は2500mかもしれないし、4200mかもしれない。

他の例題で考えてみる

まず、$x=2$ なら $x^2=4$ は必ず成り立ちます。

このとき、$x=2$ なら $x^2=4$ は「必ず成り立つ」＝「十分である」から、十分条件です。

今度は $x^2=4$ は $x=\pm2$ だから$x=2$ ではない場合が出てきます。

$x=2$ にとって、「$x$ が $2$ か $-2$ のどちらかである」は、必要な条件ではあっても必ず成り立つとは言えない＝十分な条件とは言えない。だから、必要条件です。

はじめのうちは公式として対処する

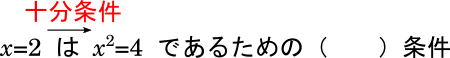
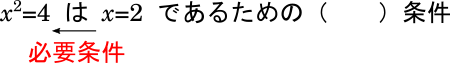
矢印の意味は必ず成り立つということです。「成り立つときもあるけど、成り立たないときもある」はアウトです。

そして、右向き矢印が成り立つなら十分条件。左向き矢印が成り立つなら必要条件と答えれば良いのです。

また、どちらの矢印も必ず成り立つなら、必要十分条件。どちらも必ず成り立たないときは、必要条件でも十分条件でもない、となります。