【数Ⅱ図形と方程式】点と直線の距離の公式をビジュアルで覚える

点と直線の距離の公式ってすぐに忘れる。

ああ。

点$(x_1,y_1)$と$ax+by+c=0$の距離は

$\displaystyle\frac{|ax_1+by_1+c|}{\sqrt{a^2+b^2}}$

ってヤツでしょ？

[te]複雑な公式はステップを踏んで覚えるといいよ。

点と直線の距離の公式は３ステップで覚える

公式というより、実際の式でつかむ方がいいね。

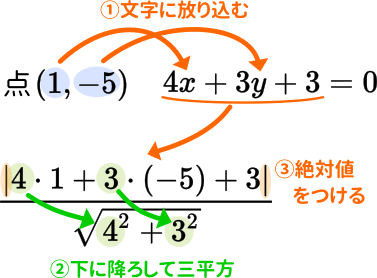
ここでは、例題で点$(1,-5)$と直線$4x+3y+3=0$でやってみるよ。

まず、①式の$x$と$y$に点の座標をそれぞれ放り込んでやる。

②次に$x$と$y$の前についている数字を下に降ろして、三平方の定理の形にする。

③距離は必ず正の値じゃないといけないから、絶対値を付ける。

えーと、

①$\displaystyle 4\cdot1+3\cdot(-5)+3$

②$\displaystyle \frac{4\cdot1+3\cdot(-5)+3}{\sqrt{4^2+3^2}}$

③$\displaystyle \frac{|4\cdot1+3\cdot(-5)+3|}{\sqrt{4^2+3^2}}$

できた！

[te]

あとは、

$=\displaystyle \frac{|4-14+3|}{\sqrt{25}}$

$=\displaystyle \frac{|-8|}{5}=\frac{8}{5}$(答え)

複雑な公式を覚えるコツ

この手の公式はなかなか覚えられないものですよね。数学は公式がいっぱいある上にいくつか複雑な公式があって、何回やっても覚えられない！と思っている人も多いと思います。三角関数の加法定理などは呪文のように唱えて覚えるものですが、今回の公式は唱えて覚えるのも難しそうです。

そういうときに大事なのは、全体をぼんやり眺めるのではなく部分に分解して、いくつかのステップに分けて段階を踏んで組み立てていくことです。人間の脳って、複雑な形を一度に処理することはできないけど、それを手順化してプロセスとして覚える方法だとうまく覚えられます。

今回は３ステップで手順化してみました。一つ一つの手順は「なぜ？」と考えてもしょうがないようなものですね（絶対値のところだけ納得いく理由がありますが）。それでも、手順化さえしてしまえば案外あっさりと覚えられるようになると思います。

他の公式でもこの考え方は使えるので、いろいろ試してみてください。