【数III極座標・極方程式】極方程式の授業を聞いてなかったのでおさらいする




方程式と極方程式
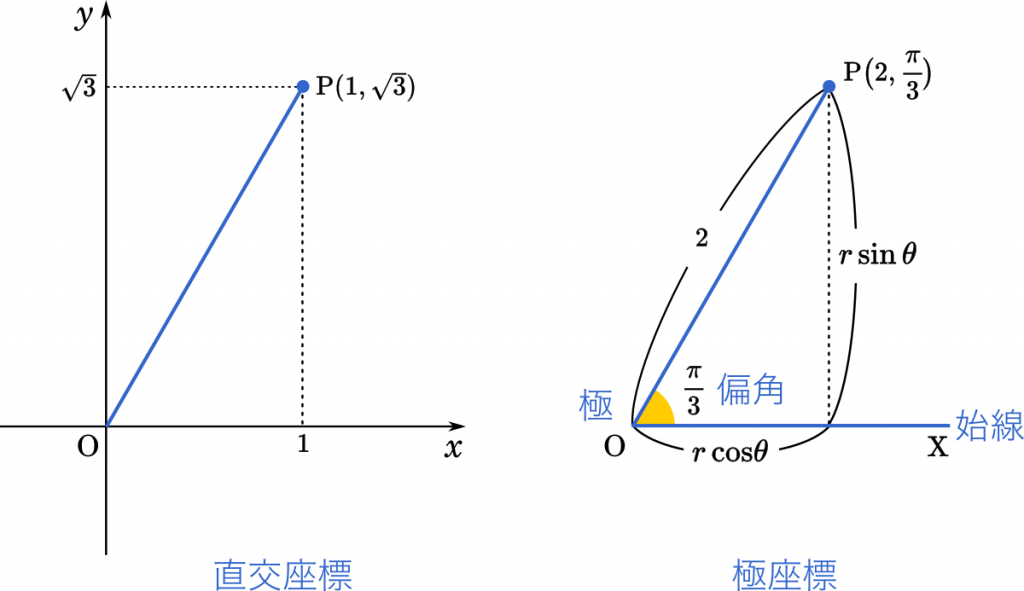
まずは,直交座標と極座標の違いから。
上の図の点 P は同じものですが,直交座標と極座標の2通りで表しています。
直交座標は今まで習ってきたもので,$x$ 座標と $y$ 座標で点の位置を決めます。
一方,極座標は OP の長さ $r$ と偏角 $\theta$ で点の位置を決めます。
このように,同じ点を表すのに2通りの方法があるということです。点 P を直交座標で表すなら P$(1,\sqrt{3})$ で,極座標なら P$\big(2,\dfrac{\pi}{3}\big)$ です。
このとき,極座標を直交座標に直すなら
$x=r\cos\theta$,$y=r\sin\theta$
となります。


極座標を直交座標で表す
[問題] 極座標の点 $(3,\pi)$ を直交座標で表せ。

$x=r\cos\theta$
$=3\cos\pi=3(-1)=-3$
$y=r\sin\theta$
$=3\sin\pi=3\cdot0=0$
したがって,直交座標は $(\bf{-3,0})$ (答え)
直交座標を極座標で表す
[問題] 直交座標の点 $(\sqrt{3},1)$ を極座標で表せ。
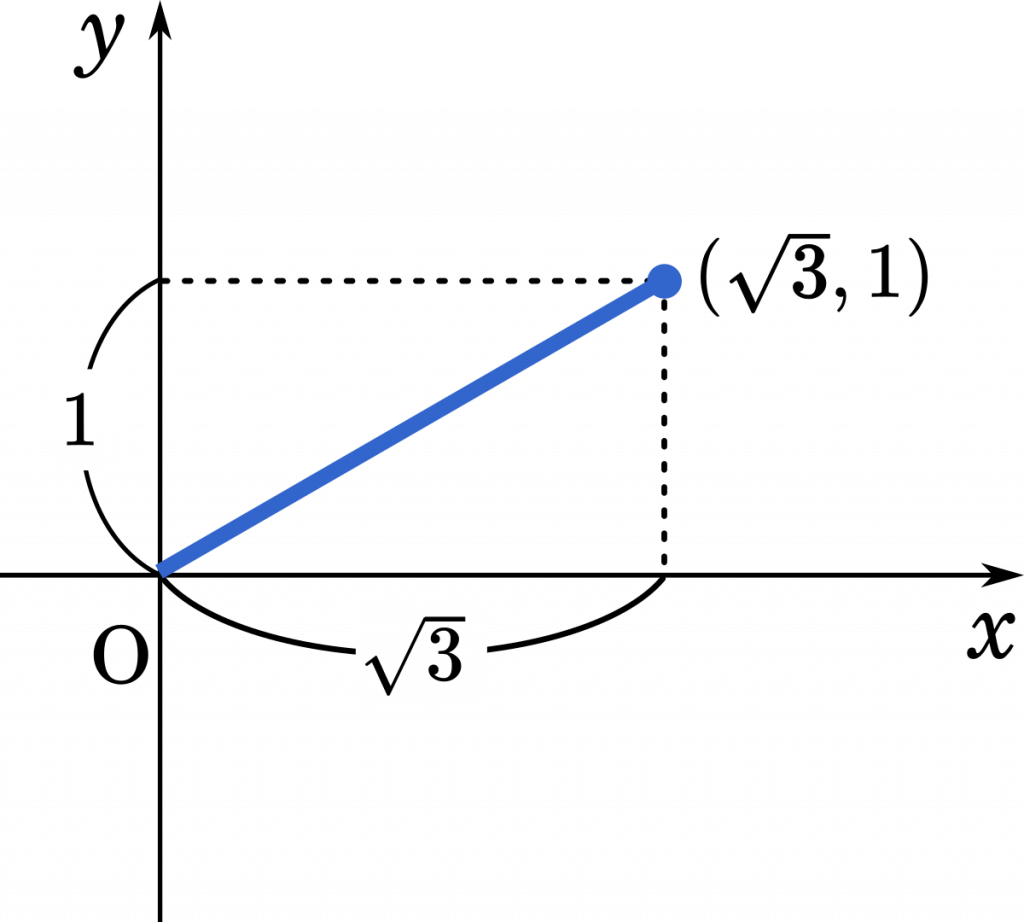
$r$ は三平方の定理を使って求めます。
$r=\sqrt{1^2+(\sqrt{3})^2}=2$
ただし,ここは $1:2:\sqrt{3}$ の三角形だから,三平方の定理を使わなくても $r=2$ はすぐに求められます。
同様に,偏角 $\theta=\cfrac{\pi}{6}$ です。
したがって,極座標は $\big(\bf{2,\dfrac{\pi}{6}}\big)$ (答え)
極方程式
今まで習ってきた直交座標で,直線を表す式と言えば
$y=ax+b$
でした。この式は,$x$ にある値を代入すると $y$ の値を求めることができます。これを方程式と言いました。$x$ の値によって $y$ の値が決まるという関係です。
一方で,$\theta$ の値によって $r$ の値が決まるという関係で表す式を極方程式と言います。基本的に,極方程式は左辺が $r$,右辺に $\theta$ の含まれる式で表します。
ただし,例外もあります。
例えば,半径 1 の円は方程式なら
$x^2+y^2=1$
と表し,これを極方程式で表すと
$r=1$
となります。これは,$\theta$ の値に関係なく,$r=1$ であるということです。
これは,直交座標のときに,$x$ 軸に平行で $y$ の値が 2 である直線を $y=2$ と表すようなものです。極方程式でも式に必ず $r$ と $\theta$ が含まれるわけではありません。
また,原点を通り点 $(1,\sqrt{3})$ を通る直線は方程式では
$y=\sqrt{3}x$
と表し,これを極座標で表すと
$\theta=\cfrac{\pi}{3}$
となります。これは,直線上の点ならば,$r$ の値に関係なく,$\theta=\cfrac{\pi}{3}$ であるということです。
直線を極方程式で表す
[問題] 極座標が $(4,0)$ である点 A を通り,始線 OX と $\dfrac{\pi}{6}$ の角をなす直線の極方程式を求めよ。
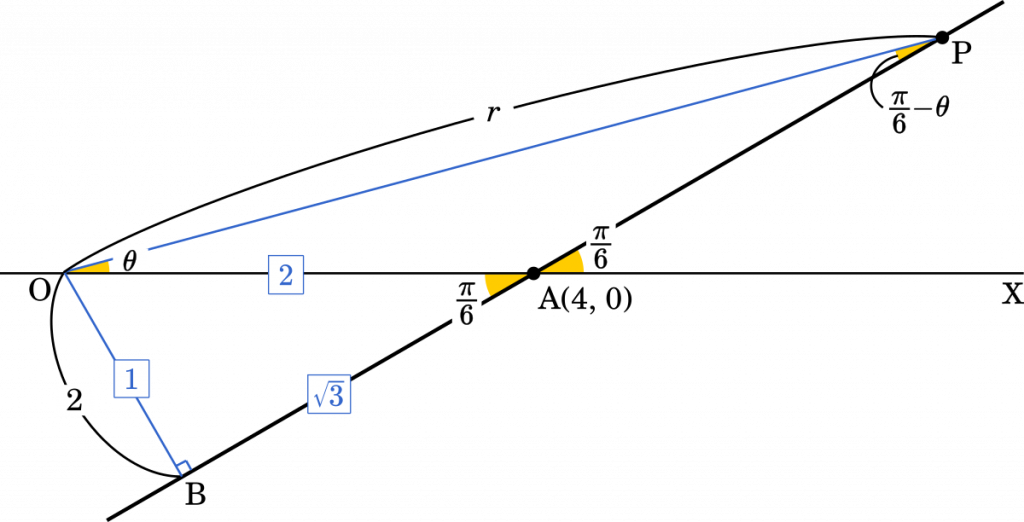
いきなりですが,少し難易度の高い問題です。
まず,直線上に点 P$(r,\theta)$ を置きます。そして,△OPB が直角三角形になるように点 B を置きます。

こうすると,△OAB と △OPB の 2 つの直角三角形ができます。直角三角形を作るのは三角比を使いたいからです。
△OAB は $1:2:\sqrt{3}$ の直角三角形だから,OA = 4 から,OB = 2 が分かります。
それを用いて,今度は △OPB を考えます。このとき,∠OPB の大きさは $\dfrac{\pi}{6}-\theta$ です。

△OPA で考えると,$\dfrac{\pi}{6}$ は三角形の外角になっています。つまり,∠OPA を $x$ とするなら
$\theta+x=\cfrac{\pi}{6}$
$x=\cfrac{\pi}{6}-\theta$
となるのです。


話を戻すと,△OPB において,今度は PB を底辺として考えると,OB は高さとなるので
$r\sin\big(\dfrac{\pi}{6}-\theta\big)=2$ (答え)
上で述べた,$\text{斜辺}\times\cfrac{\text{高さ}}{\text{斜辺}}=\text{高さ}$ の式です。
これで終わりです。この式をそのまま答えとするか,変形して
$r=\cfrac{2}{\sin\big(\cfrac{\pi}{6}-\theta\big)}$
を答えとします。
この問題は直線を引いたものの何をやっていいのか分からなくなることが多いです。最初に直角三角形を2つ作るということを覚えておくと,突破口が開けるでしょう。



極方程式のとき,一般的に $\theta$ の変域は示しませんが,今回の問題で言えば,実際は $-\cfrac{5}{6}\pi<\theta<\cfrac{\pi}{6}$ という変域が存在しています。
点 P を原点から限りなく遠いところに置くことを考えると,直線 OP と直線 AP は限りなく平行に近づいていきます。しかし,平行に近づくというだけで完全に平行になるわけではありません。こうして,$r$ が大きくなるにつれ,$\theta$ は限りなく $\cfrac{\pi}{6}$ に近づいても,$\cfrac{\pi}{6}$ そのものになったり,それを超えたりすることはありません。$-\cfrac{5}{6}\pi$ の方も話は同じです。
どちらかと言うと,解法をパターンとして暗記しておくタイプの問題なので,解きなおして手順を暗記しましょう。
SNSでシェア